|
|
|
| (10 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| | + | <metakeywords>Информатика, класc, урок, на тему, 9 класc, Имитационные модели в электронных таблицах, модель, кодирование, процессор</metakeywords> |
| | + | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 9 класс|Информатика 9 класс]]>>Информатика: Имитационные модели в электронных таблицах''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 9 класс|Информатика 9 класс]]>>Информатика: Имитационные модели в электронных таблицах''' |
| | + | |
| | + | <br> <br> |
| | + | |
| | + | '''§ 24. Имитационные модели в электронной таблице''' |
| | + | |
| | + | <br> Основные темы параграфа: |
| | + | |
| | + | ♦ что такое имитационная модель; <br>♦ пример имитационного моделирования в '''[[Что такое электронная таблица|электронных таблицах]]'''. |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <metakeywords>Информатика, класc, урок, на тему, 9 класc, Имитационные модели в электронных таблицах.</metakeywords>ИМИТАЦИОННЫЕ МОДЕЛИ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ | + | '''Что такое имитационная модель''' |
| | + | |
| | + | В предыдущем параграфе вы познакомились с примером реализации в электронной таблице математической модели. Сейчас рассмотрим пример реализации другого типа модели, которая называется имитационной моделью. |
| | + | |
| | + | Об имитационных '''[[Информационное моделирование на компьютере|моделях]]''' говорилось в § 9. Вспомним данное там определение: |
| | + | |
| | + | ''Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.'' |
| | + | |
| | + | <br> '''Пример имитационного моделирования в электронных таблицах''' |
| | + | |
| | + | Как и в предыдущем параграфе, пример возьмем из класса моделей, описывающих эволюцию популяций. |
| | + | |
| | + | Пусть на определенном пространстве случайным образом расселяются живые организмы. В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает. Эти процессы протекают в соответствии с законами эволюции. Законы эволюции в описании модели представляются в виде формальных правил. Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений. |
| | + | |
| | + | Сначала рассмотрим простейший вариант задачи: жизненное пространство одномерное. Это значит, живые организмы расселяются вдоль линии. Будем считать жизненное пространство ограниченным, т. е. рассмотрим отрезок. Отрезок разделяется на ячейки, в пределах каждой из которых может поселиться один организм. Договоримся, что самые крайние ячейки не заселяются. Они определяют границу жизненного пространства. |
| | + | |
| | + | На рис. 4.3 показано первоначальное расселение организмов на поле, состоящем из 20 ячеек. Организмы поселились в ячейках с номерами 5, 8 и 12. Ячейки 1 и 20 всегда должны быть пустыми. |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <u>§ 24. Имитационные модели в электронной таблице</u>
| + | [[Image:Informatika 9 138z.jpg|550px|Первоначальное расселение организмов]]<br> |
| | | | |
| - | Основные темы параграфа:
| + | <br> |
| | | | |
| - | ♦ что такое имитационная модель; <br>♦ пример имитационного моделирования в электронных таблицах.
| + | Теперь сформулируем законы эволюции. В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет. В живой ячейке жизнь может либо сохраниться, либо исчезнуть. На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа. Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения). Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой. |
| | | | |
| - | ''Что такое имитационная модель''
| + | Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других. У ячейки номер 2 соседи: 1, 3 и 4. Но ячейка 1 всегда пустая. У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5). Аналогичная ситуация у крайних правых ячеек. |
| | | | |
| - | В предыдущем параграфе вы познакомились с примером реализации в электронной таблице математической модели. Сейчас рассмотрим пример реализации другого типа модели, которая называется имитационной моделью.
| + | То, что сказано выше, есть модельное описание процесса эволюции популяции. Формализуем это описание. Распределение живых организмов по ячейкам будем '''[[Презентация урока на тему: Кодирование|кодировать]]''' последовательностью из нулей и единиц. Ноль обозначает пустую ячейку, единица — живую. Например, расселение, отображенное на рис. 4.3, кодируется следующим образом: |
| | | | |
| - | Об имитационных моделях говорилось в § 9. Вспомним данное там определение:
| + | 00001001000100000000 |
| | | | |
| - | ''Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.'' | + | Обозначим буквой n номер ячейки, а значение двоичного числа, соответствующего этой ячейке в текущем поколении, обозначим ''R''(n). В рассматриваемом примере ''R''(5) = ''R''(8) = ''R''(12) = 1. Все остальные значения ячеек равны нулю. |
| | | | |
| - | ''Пример имитационного моделирования в электронных таблицах'' | + | Значения кода в ''n''-й ячейке для следующего поколения будем обозначать ''S''(''n''). Внимательно проанализировав сформулированные выше правила эволюции, приходим к следующей формуле: |
| | | | |
| - | Как и в предыдущем параграфе, пример возьмем из класса моделей, описывающих эволюцию популяций.
| + | Если 1 <u><</u> ''R''(''n'' - 2) +''R''(''n'' - 1) + ''R''(''n'') + ''R''(''n'' + 1) + ''R''(''n'' + 2) <u><</u> 3,<br>то ''S''(''n'') = 1, иначе ''S''(''n'') = 0. |
| | | | |
| - | Пусть на определенном пространстве случайным образом расселяются живые организмы. В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает. Эти процессы протекают в соответствии с законами эволюции. Законы эволюции в описании модели представляются в виде формальных правил. Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.
| + | Эта формула работает для значений ''n'' от 3 до 18. Всегда: ''S''(1) = ''S''(20) = 0. Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе, чтобы оставить справедливой данную формулу для всех ячеек жизненного пространства. Для этого к отрезку добавим по одной фиктивной ячейке справа и слева. Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для ''n'' от 2 до 19. |
| | | | |
| - | Сначала рассмотрим простейший вариант задачи: жизненное пространство одномерное. Это значит, живые организмы расселяются вдоль линии. Будем считать жизненное пространство ограниченным, т. е. рассмотрим отрезок. Отрезок разделяется на ячейки, в пределах каждой из которых может поселиться один организм. Договоримся, что самые крайние ячейки не заселяются. Они определяют границу жизненного пространства.
| + | Итак, модель построена и формализована. Однако имитационной моделью она станет только в результате реализации с помощью какого-то программного компьютерного средства. В качестве такого средства выберем табличный '''[[Текстовый процессор MS Word|процессор]]'''. |
| | | | |
| - | На рис. 4.3 показано первоначальное расселение организмов на поле, состоящем из 20 ячеек. Организмы поселились в ячейках с номерами 5, 8 и 12. Ячейки 1 и 20 всегда должны быть пустыми.<br><br>Теперь сформулируем законы эволюции. В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет. В живой ячейке жизнь может либо сохраниться, либо исчезнуть. На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа. Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения). Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.
| + | Моделью жизненного пространства будет строка электронной таблицы. Первая строка — первое поколение, вторая строка — второе поколение и т. д. Тогда номера ячеек будут идентифицироваться именами столбцов таблицы. Ячейка номер 0 — столбец А, ячейка 1 — столбец В и т. д., ячейка 21 — столбец F. |
| | | | |
| - | Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других. У ячейки номер 2 соседи: 1, 3 и 4. Но ячейка 1 всегда пустая. У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5). Аналогичная ситуация у крайних правых ячеек.
| + | В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1. Незаполненные ячейки по умолчанию приравниваются к нулю. |
| | | | |
| - | То, что сказано выше, есть модельное описание процесса эволюции популяции. Формализуем это описание. Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц. Ноль обозначает пустую ячейку, единица — живую. Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:
| + | Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу: |
| | | | |
| - | 00001001000100000000
| + | ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 >=1; <br>А1 + В1 + С1 + D1 + Е1 <= 3); 1; 0) |
| | | | |
| - | Обозначим буквой n номер ячейки, а значение двоичного числа, соответствующего этой ячейке в текущем поколении, обозначим ''R''(n). В рассматриваемом примере ''R''(5) = ''R''(8) = ''R''(12) = 1. Все остальные значения ячеек равны нулю.
| + | Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении. |
| | | | |
| - | Значения кода в ''n''-й ячейке для следующего поколения будем обозначать ''S''(п). Внимательно проанализировав сформулированные выше правила эволюции, приходим к следующей формуле:
| + | Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно. |
| | | | |
| - | Если 1 <u><</u> ''R''(''n'' - 2) +''R''(''n'' - 1) + ''R''(''n'') + ''R''(''n'' + 1) + ''R''(''n'' + 2) <u><</u> 3,<br>то ''S''(''n'') = 1, иначе ''S''(''n'') = 0.
| + | На рис. 4.4 показаны результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения. Все очень наглядно. Обратите внимание, как драматично развивались события! В шестом поколении наступило состояние перенаселения, В результате в седьмом поколении вымерли все организмы, кроме крайних. Их спасло свободное пространство слева и справа. От них пошла новая волна жизни! |
| | | | |
| - | Эта формула работает для значений n от 3 до 18. Всегда: S(1) = S(20) = 0. Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе, чтобы оставить справедливой данную формулу для всех ячеек жизненного пространства. Для этого к отрезку добавим по одной фиктивной ячейке справа и слева. Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для п от 2 до 19.<br>Итак, модель построена и формализована. Однако имитационной моделью она станет только в результате реализации с помощью какого-то программного компьютерного средства. В качестве такого средства выберем табличный процессор.<br>Моделью жизненного пространства будет строка электронной таблицы. Первая строка — первое поколение, вторая строка — второе поколение и т. д. Тогда номера ячеек будут идентифицироваться именами столбцов таблицы. Ячейка но¬мер 0 — столбец А, ячейка 1 — столбец В и т. д., ячейка 21 — столбец F.<br><br><br>В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1. Незаполненные ячейки по умолчанию приравниваются к нулю.<br>Теперь в ячейки второй строки нужно записать формулы, Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:<br>ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 >=1; <br>А1 + В1 + С1 + D1 + Е1 <= 3); 1; 0)<br>Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.<br>Чтобы получить третье поколение, достаточно скопиро-вать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.<br>На рис. 4.4 показаны результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения. Все очень наглядно. Обратите внимание, как драматично развивались события! В шестом поколении наступило состояние перенаселения, В результате в седьмом поколении вымерли все организмы, кроме крайних. Их спасло свободное пространство слева и справа. От них пошла новая волна жизни!<br><br>Рассмотренная задача является упрощенным (одномерным) вариантом известной модели Дж. Конуэя, которая nназывается «Жизнь». В этой модели эволюция популяции живых организмов происходит в двумерном простран¬стве. Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния со¬седних клеток. Но теперь правила эволюции такие: если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения; если же живых соседей меньше двух, то она погибает от одиночества. В пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.<br>Попробуйте самостоятельно получить имитационную модель для этой задачи в среде электронной таблицы. Последо¬вательность действий будет аналогичной рассмотренной в примере. По-прежнему для перехода к новому поколению нужно использовать метод копирования диапазона. Но только теперь придется копировать не линейный диапазон, а прямоугольный.<br>Коротко о главном<br>Рассмотренная имитационная модель эволюционного типа позволяет проследить за изменениями в расселении живых организмов со сменой поколений.<br>Удобство применения электронной таблицы для имитационного моделирования заключается в простоте реализации вычислительного алгоритма и наглядности представления результатов.<br><br>Вопросы и задания<br>1. Для каких задач используется метод компьютерного имитаци¬онного моделирования?<br>2. В чем отличие эволюционной задачи, решавшейся методом ма¬тематического моделирования в § 23* от задачи, решавшейся в данном параграфе методом имитационного моделирования?<br>3. Проведите вычислительный эксперимент на линейной имита¬ционной модели для различных вариантов исходного расселе-<br>ния организмов. Ответьте на вопросы:<br>1) Возможно ли такое расселение, при котором все организмы в конце концов вымрут?<br>2) Не ведет ли любое расселение в конечном итоге к одной и той же последовательности поколений?<br>3) Что меняется с изменением размера жизненного пространства?<br>4*. Постройте в электронной таблице двумерную модель Дж. Конуэя «Жизнь». Проведите вычислительный эксперимент с разными вариантами первоначального расселения организмов. <br>5*. Решая предыдущую задачу, попробуйте найти такие первона¬чальные расселения, которые:<br>1) обречены на гибель;<br>2) не меняются со сменой поколений;<br>3) ведут к периодической смене повторяющихся конфигураций расселения.<br>Чему вы должны научиться, изучив главу 4<br>Освоить один из табличных процессоров (ТП), имеющихся в компьютерном классе.<br>Входить в программу, открывать файл с готовой электронной таблицей (ЭТ), сохранять ЭТ, выходить из программы.<br>Менять режимы отображения информации в ЭТ.<br>Перемещать табличный курсор, редактировать содержи-мое ячеек ЭТ.<br>Вводить в ячейки таблицы тексты, числа, формулы.<br>Выполнять основные операции манипулирования с диапазонами ЭТ: копирование, удаление, вставку, сортировку.<br>Получать диаграммы с помощью графических средств ТП.<br>Создавать собственную ЭТ для несложных табличных расчетов.<br><br> ''И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс<br>Отослано читателями из интернет-сайтов''
| + | [[Image:Informatika 9 140z.jpg|550px|Имитация в электронной таблице эволюции поколений]]<br> |
| | | | |
| - | <br> <sub>Информатика в школе, скачать бесплатно тесты, полный курс информатики, онлайн библиотека с книгами и учебниками по информатике на скачку, планы уроков информатики 9 класс</sub> | + | [[Image:Informatika 9 141c.jpg|240px|Одномерный вариант модели]]<br> |
| | + | |
| | + | Рассмотренная задача является упрощенным (одномерным) вариантом известной модели Дж. Конуэя, которая называется «Жизнь». В этой модели эволюция популяции живых организмов происходит в двумерном пространстве. Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток. Но теперь правила эволюции такие: если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения; если же живых соседей меньше двух, то она погибает от одиночества. В пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа. |
| | + | |
| | + | Попробуйте самостоятельно получить имитационную модель для этой задачи в среде электронной таблицы. Последовательность действий будет аналогичной рассмотренной в примере. По-прежнему для перехода к новому поколению нужно использовать метод копирования диапазона. Но только теперь придется копировать не линейный диапазон, а прямоугольный. |
| | + | |
| | + | |
| | + | |
| | + | '''Коротко о главном''' |
| | + | |
| | + | Рассмотренная имитационная модель эволюционного типа позволяет проследить за изменениями в расселении живых организмов со сменой поколений. |
| | + | |
| | + | Удобство применения электронной таблицы для имитационного моделирования заключается в простоте реализации вычислительного алгоритма и наглядности представления результатов. |
| | + | |
| | + | |
| | + | |
| | + | '''Вопросы и задания''' |
| | + | |
| | + | ''1. Для каких задач используется метод компьютерного имитационного моделирования?<br>2. В чем отличие эволюционной задачи, решавшейся методом математического моделирования в § 23, от задачи, решавшейся в данном параграфе методом имитационного моделирования?<br>3. Проведите вычислительный эксперимент на линейной имитационной модели для различных вариантов исходного расселения организмов. Ответьте на вопросы:<br>1) Возможно ли такое расселение, при котором все организмы в конце концов вымрут?<br>2) Не ведет ли любое расселение в конечном итоге к одной и той же последовательности поколений?<br>3) Что меняется с изменением размера жизненного пространства?<br>4*. Постройте в электронной таблице двумерную модель Дж. Конуэя «Жизнь». Проведите вычислительный эксперимент с разными вариантами первоначального расселения организмов. <br>5*. Решая предыдущую задачу, попробуйте найти такие первоначальные расселения, которые:<br>1) обречены на гибель;<br>2) не меняются со сменой поколений;<br>3) ведут к периодической смене повторяющихся конфигураций расселения.'' |
| | + | |
| | + | |
| | + | |
| | + | '''Чему вы должны научиться, изучив главу 4''' |
| | + | |
| | + | • Освоить один из табличных процессоров (ТП), имеющихся в компьютерном классе.<br>• Входить в программу, открывать файл с готовой электронной таблицей (ЭТ), сохранять ЭТ, выходить из [http://xvatit.com/it/fishki-ot-itshki/ '''программы'''].<br>• Менять режимы отображения информации в ЭТ.<br>• Перемещать табличный курсор, редактировать содержимое ячеек ЭТ.<br>• Вводить в ячейки таблицы тексты, числа, формулы.<br>• Выполнять основные операции манипулирования с диапазонами ЭТ: копирование, удаление, вставку, сортировку.<br>• Получать диаграммы с помощью графических средств ТП.<br>• Создавать собственную ЭТ для несложных табличных расчетов. |
| | + | |
| | + | <br> ''И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс<br>Отослано читателями из интернет-сайтов'' |
| | + | |
| | + | <br> <sub>Информатика в школе, скачать бесплатно тесты, полный курс [[Інформатика|информатики]], [[Гипермаркет знаний - первый в мире!|онлайн библиотека]] с книгами и учебниками по информатике на скачку, планы уроков [[Информатика 9 класс|информатики 9 класс]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 11:41, 3 июля 2012
Гипермаркет знаний>>Информатика>>Информатика 9 класс>>Информатика: Имитационные модели в электронных таблицах
§ 24. Имитационные модели в электронной таблице
Основные темы параграфа:
♦ что такое имитационная модель;
♦ пример имитационного моделирования в электронных таблицах.
Что такое имитационная модель
В предыдущем параграфе вы познакомились с примером реализации в электронной таблице математической модели. Сейчас рассмотрим пример реализации другого типа модели, которая называется имитационной моделью.
Об имитационных моделях говорилось в § 9. Вспомним данное там определение:
Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.
Пример имитационного моделирования в электронных таблицах
Как и в предыдущем параграфе, пример возьмем из класса моделей, описывающих эволюцию популяций.
Пусть на определенном пространстве случайным образом расселяются живые организмы. В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает. Эти процессы протекают в соответствии с законами эволюции. Законы эволюции в описании модели представляются в виде формальных правил. Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.
Сначала рассмотрим простейший вариант задачи: жизненное пространство одномерное. Это значит, живые организмы расселяются вдоль линии. Будем считать жизненное пространство ограниченным, т. е. рассмотрим отрезок. Отрезок разделяется на ячейки, в пределах каждой из которых может поселиться один организм. Договоримся, что самые крайние ячейки не заселяются. Они определяют границу жизненного пространства.
На рис. 4.3 показано первоначальное расселение организмов на поле, состоящем из 20 ячеек. Организмы поселились в ячейках с номерами 5, 8 и 12. Ячейки 1 и 20 всегда должны быть пустыми.

Теперь сформулируем законы эволюции. В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет. В живой ячейке жизнь может либо сохраниться, либо исчезнуть. На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа. Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения). Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.
Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других. У ячейки номер 2 соседи: 1, 3 и 4. Но ячейка 1 всегда пустая. У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5). Аналогичная ситуация у крайних правых ячеек.
То, что сказано выше, есть модельное описание процесса эволюции популяции. Формализуем это описание. Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц. Ноль обозначает пустую ячейку, единица — живую. Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:
00001001000100000000
Обозначим буквой n номер ячейки, а значение двоичного числа, соответствующего этой ячейке в текущем поколении, обозначим R(n). В рассматриваемом примере R(5) = R(8) = R(12) = 1. Все остальные значения ячеек равны нулю.
Значения кода в n-й ячейке для следующего поколения будем обозначать S(n). Внимательно проанализировав сформулированные выше правила эволюции, приходим к следующей формуле:
Если 1 < R(n - 2) +R(n - 1) + R(n) + R(n + 1) + R(n + 2) < 3,
то S(n) = 1, иначе S(n) = 0.
Эта формула работает для значений n от 3 до 18. Всегда: S(1) = S(20) = 0. Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе, чтобы оставить справедливой данную формулу для всех ячеек жизненного пространства. Для этого к отрезку добавим по одной фиктивной ячейке справа и слева. Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для n от 2 до 19.
Итак, модель построена и формализована. Однако имитационной моделью она станет только в результате реализации с помощью какого-то программного компьютерного средства. В качестве такого средства выберем табличный процессор.
Моделью жизненного пространства будет строка электронной таблицы. Первая строка — первое поколение, вторая строка — второе поколение и т. д. Тогда номера ячеек будут идентифицироваться именами столбцов таблицы. Ячейка номер 0 — столбец А, ячейка 1 — столбец В и т. д., ячейка 21 — столбец F.
В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1. Незаполненные ячейки по умолчанию приравниваются к нулю.
Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:
ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 >=1;
А1 + В1 + С1 + D1 + Е1 <= 3); 1; 0)
Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.
Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.
На рис. 4.4 показаны результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения. Все очень наглядно. Обратите внимание, как драматично развивались события! В шестом поколении наступило состояние перенаселения, В результате в седьмом поколении вымерли все организмы, кроме крайних. Их спасло свободное пространство слева и справа. От них пошла новая волна жизни!
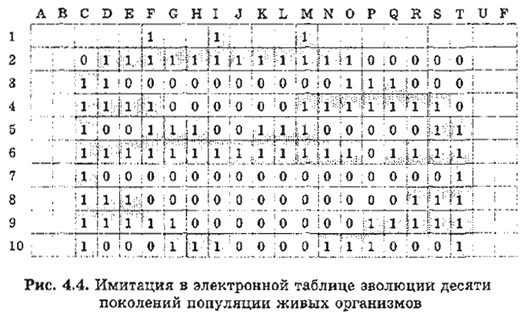
Рассмотренная задача является упрощенным (одномерным) вариантом известной модели Дж. Конуэя, которая называется «Жизнь». В этой модели эволюция популяции живых организмов происходит в двумерном пространстве. Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток. Но теперь правила эволюции такие: если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения; если же живых соседей меньше двух, то она погибает от одиночества. В пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.
Попробуйте самостоятельно получить имитационную модель для этой задачи в среде электронной таблицы. Последовательность действий будет аналогичной рассмотренной в примере. По-прежнему для перехода к новому поколению нужно использовать метод копирования диапазона. Но только теперь придется копировать не линейный диапазон, а прямоугольный.
Коротко о главном
Рассмотренная имитационная модель эволюционного типа позволяет проследить за изменениями в расселении живых организмов со сменой поколений.
Удобство применения электронной таблицы для имитационного моделирования заключается в простоте реализации вычислительного алгоритма и наглядности представления результатов.
Вопросы и задания
1. Для каких задач используется метод компьютерного имитационного моделирования?
2. В чем отличие эволюционной задачи, решавшейся методом математического моделирования в § 23, от задачи, решавшейся в данном параграфе методом имитационного моделирования?
3. Проведите вычислительный эксперимент на линейной имитационной модели для различных вариантов исходного расселения организмов. Ответьте на вопросы:
1) Возможно ли такое расселение, при котором все организмы в конце концов вымрут?
2) Не ведет ли любое расселение в конечном итоге к одной и той же последовательности поколений?
3) Что меняется с изменением размера жизненного пространства?
4*. Постройте в электронной таблице двумерную модель Дж. Конуэя «Жизнь». Проведите вычислительный эксперимент с разными вариантами первоначального расселения организмов.
5*. Решая предыдущую задачу, попробуйте найти такие первоначальные расселения, которые:
1) обречены на гибель;
2) не меняются со сменой поколений;
3) ведут к периодической смене повторяющихся конфигураций расселения.
Чему вы должны научиться, изучив главу 4
• Освоить один из табличных процессоров (ТП), имеющихся в компьютерном классе.
• Входить в программу, открывать файл с готовой электронной таблицей (ЭТ), сохранять ЭТ, выходить из программы.
• Менять режимы отображения информации в ЭТ.
• Перемещать табличный курсор, редактировать содержимое ячеек ЭТ.
• Вводить в ячейки таблицы тексты, числа, формулы.
• Выполнять основные операции манипулирования с диапазонами ЭТ: копирование, удаление, вставку, сортировку.
• Получать диаграммы с помощью графических средств ТП.
• Создавать собственную ЭТ для несложных табличных расчетов.
И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов
Информатика в школе, скачать бесплатно тесты, полный курс информатики, онлайн библиотека с книгами и учебниками по информатике на скачку, планы уроков информатики 9 класс
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













