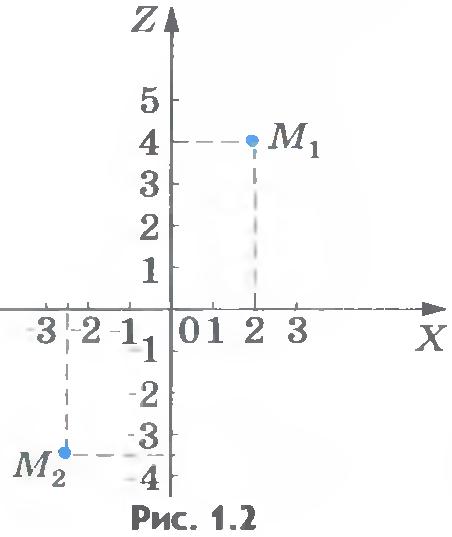|
|
|
| (2 промежуточные версии не показаны) | | Строка 3: |
Строка 3: |
| | <br> <metakeywords>Физика, 10 клас, Положение точки, в пространстве</metakeywords> | | <br> <metakeywords>Физика, 10 клас, Положение точки, в пространстве</metakeywords> |
| | | | |
| - | Чтобы решить задачу о движении тела, прежде всего надо уметь определять, или, что одно и то же, задавать, положение его в пространстве. Как же определяют положение точки?<br> Наблюдая за любым телом, мы замечаем, что его положение в один и тот же момент времени относительно различных тел различно. Например, космический корабль, запущенный с космодрома Байконур, занимает совершенно различные положения относительно Земли, Луны и Солнца. Поэтому в данном случае обязательно надо указать ''физическое тело, относительно которого задается положение данного тела или же данной точки''. Такое тело называют '''телом отсчета'''.<br> Тело отсчета можно выбрать произвольно. Им может быть космодром, самолет, в котором мы летим, космический корабль, Земля, Солнце, звезды и т. д. Но относительно различных точек тела отсчета положение любого другого тела или точки тоже различно. Если, например, за тело отсчета принять Землю, то положение спутника Земли относительно Москвы будет иным, нежели относительно космодрома Байконур. Строго говоря, мы должны указать, относительно какой точки выбранного тела отсчета задается положение данной точки или тела.<br> Если тело отсчета выбрано, то относительно него положение точки можно задать с помощью ''координат'' или ''радиус-вектора''. Выбор системы отсчета и системы координат должен быть разумным, чтобы описание движения тела выглядело достаточно просто, но в то же время мы могли бы ответить на все вопросы задачи.<br> Рассмотрим эти два способа задания положения точки.<br> '''Задание положения точки с помощью координат'''. Из курса математики вы знаете, что положение точки на плоскости можно задать с помощью двух чисел, которые называются координатами этой точки. Для этого, как известно, можно на плоскости провести две пересекающиеся взаимно перпендикулярные оси, например оси ''ОХ'' и ''ОY''. Точку пересечения осей называют началом координат, а сами оси - '''координатными осями'''.<br> Координаты точки ''М<sub>1</sub> ''(''рис.1.2'') равны ''x<sub>1</sub>'' = 2,''у<sub>1</sub>'' = 4; координаты точки ''М<sub>2</sub>'' равны ''х<sub>2</sub>'' = -2,5, ''у<sub>2</sub>'' = -3,5. | + | Чтобы решить задачу о движении тела, прежде всего надо уметь определять, или, что одно и то же, задавать, положение его в пространстве. Как же определяют положение точки?<br> Наблюдая за любым телом, мы замечаем, что его положение в один и тот же момент времени относительно различных тел различно. Например, космический корабль, запущенный с космодрома Байконур, занимает совершенно различные положения относительно Земли, [[Почему на Луне не живут люди|Луны]] и Солнца. Поэтому в данном случае обязательно надо указать ''физическое тело, относительно которого задается положение данного тела или же данной точки''. Такое тело называют '''телом отсчета'''.<br> Тело отсчета можно выбрать произвольно. Им может быть космодром, самолет, в котором мы летим, космический корабль, Земля, Солнце, звезды и т. д. Но относительно различных точек тела отсчета положение любого другого тела или точки тоже различно. Если, например, за тело отсчета принять Землю, то положение спутника Земли относительно Москвы будет иным, нежели относительно космодрома Байконур. Строго говоря, мы должны указать, относительно какой точки выбранного тела отсчета задается положение данной точки или тела.<br> Если тело отсчета выбрано, то относительно него положение точки можно задать с помощью ''[[Определение декартовых координат. Полные уроки|координат]]'' или ''радиус-вектора''. Выбор системы отсчета и системы координат должен быть разумным, чтобы описание движения тела выглядело достаточно просто, но в то же время мы могли бы ответить на все вопросы задачи.<br> Рассмотрим эти два способа задания положения точки.<br> '''Задание положения точки с помощью координат'''. Из курса математики вы знаете, что положение точки на плоскости можно задать с помощью двух чисел, которые называются координатами этой точки. Для этого, как известно, можно на плоскости провести две пересекающиеся взаимно перпендикулярные оси, например оси ''ОХ'' и ''ОY''. Точку пересечения осей называют началом координат, а сами оси - '''координатными осями'''.<br> Координаты точки ''М<sub>1</sub> ''(''рис.1.2'') равны ''x<sub>1</sub>'' = 2,''у<sub>1</sub>'' = 4; координаты точки ''М<sub>2</sub>'' равны ''х<sub>2</sub>'' = -2,5, ''у<sub>2</sub>'' = -3,5. |
| | | | |
| - | [[Image:A1.2.jpg|center|190x225px]] Положение точки ''М'' в пространстве относительно тела отсчета можно задать с помощью трех координат. Чтобы это сделать, необходимо через выбранную точку тела отсчета провести три взаимно перпендикулярные оси ''ОХ, ОY, 0Z.'' В полученной системе координат положение точки будет определяться тремя координатами ''х, у, z''.<br> Если число ''х'' положительно, то отрезок откладывается в положительном направлении оси ''ОХ ''(''рис.1.3'') (''x = ОА''). Если же число ''х'' отрицательно, то отрезок откладывается в отрицательном направлении оси ''ОХ''. Из конца этого отрезка проводят прямую, параллельную оси ''ОY'', и на этой прямой откладывают отрезок от оси ''ОХ,'' соответствующий числу ''у'' (''у = АВ'') - в положительном направлении оси ''ОY'', если число у положительно, и в отрицательном направлении оси ''ОY'', если число у отрицательно. | + | [[Image:A1.2.jpg|center|190x225px|Положение точки в пространстве]] Положение точки ''М'' в пространстве относительно тела отсчета можно задать с помощью трех координат. Чтобы это сделать, необходимо через выбранную точку тела отсчета провести три взаимно перпендикулярные оси ''ОХ, ОY, 0Z.'' В полученной системе координат положение точки будет определяться тремя координатами ''х, у, z''.<br> Если число ''х'' положительно, то отрезок откладывается в положительном направлении оси ''ОХ ''(''рис.1.3'') (''x = ОА''). Если же число ''х'' отрицательно, то отрезок откладывается в отрицательном направлении оси ''ОХ''. Из конца этого отрезка проводят прямую, параллельную оси ''ОY'', и на этой прямой откладывают отрезок от оси ''ОХ,'' соответствующий числу ''у'' (''у = АВ'') - в положительном направлении оси ''ОY'', если число у положительно, и в отрицательном направлении оси ''ОY'', если число у отрицательно. |
| | | | |
| - | [[Image:A1.3.jpg|center|214x217px]] Далее из точки ''В'' другого отрезка проводят прямую, параллельную оси ''ОZ''. На этой прямой от координатной плоскости ''ХОY'' откладывают отрезок, соответствующий числу ''z''. Направление, в котором откладывают этот отрезок, определяют так же, как и в предыдущих случаях. <br> Конец третьего отрезка и есть та точка, положение которой задается координатами ''х, у, z''.<br> Чтобы определить координаты данной точки, необходимо провести в обратной последовательности те операции, которые мы осуществляли, находя положение этой точки по ее координатам.<br> '''Задание положения точки с помощью радиус-вектора'''. Положение точки можно задать не только с помощью координат, но и с помощью радиус-вектора. '''Радиус-вектор''' - это направленный отрезок, проведенный из начала координат в данную точку.<br> Радиус-вектор принято обозначать буквой [[Image:a4-2.jpg]]. Длина радиус-вектора, или, что одно и то же, его модуль (''рис.1.4''), есть расстояние от начала координат до точки ''М''. | + | [[Image:A1.3.jpg|center|214x217px|Положение точки в пространстве]] Далее из точки ''В'' другого отрезка проводят [[Параллельность_прямых._Полные_уроки|прямую]], параллельную оси ''ОZ''. На этой прямой от координатной плоскости ''ХОY'' откладывают отрезок, соответствующий числу ''z''. Направление, в котором откладывают этот отрезок, определяют так же, как и в предыдущих случаях. <br> Конец третьего отрезка и есть та точка, положение которой задается координатами ''х, у, z''.<br> Чтобы определить координаты данной точки, необходимо провести в обратной последовательности те операции, которые мы осуществляли, находя положение этой точки по ее координатам.<br> '''Задание положения точки с помощью радиус-вектора'''. Положение точки можно задать не только с помощью координат, но и с помощью радиус-вектора. '''Радиус-вектор''' - это направленный отрезок, проведенный из начала координат в данную точку.<br> Радиус-вектор принято обозначать буквой [[Image:A4-2.jpg|12x21px|A4-2.jpg]]. Длина радиус-вектора, или, что одно и то же, его модуль (''рис.1.4''), есть расстояние от начала координат до точки ''М''. |
| | | | |
| - | [[Image:A1.4.jpg|center|208x195px]] Положение точки будет определено с помощью радиус-вектора только в том случае, если известны его модуль (длина) и направление в пространстве. Лишь при этом условии мы будем знать, в каком направлении от начала координат следует отложить отрезок длиной ''r'', чтобы определить положение точки.<br> Итак, положение точки в пространстве определяется ее координатами или ее радиус-вектором.<br> Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось?<br> Изобразим какую-либо ось (''рис.1.5''), например ось ''ОХ''. | + | [[Image:A1.4.jpg|center|208x195px|Положение точки в пространстве]] Положение точки будет определено с помощью радиус-вектора только в том случае, если известны его модуль (длина) и направление в пространстве. Лишь при этом условии мы будем знать, в каком направлении от начала координат следует отложить отрезок длиной ''r'', чтобы определить положение точки.<br> Итак, положение точки в пространстве определяется ее координатами или ее радиус-вектором.<br> Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось?<br> Изобразим какую-либо ось (''рис.1.5''), например ось ''ОХ''. |
| | | | |
| - | [[Image:A1.5.jpg|center|181x114px]] Опустим из начала ''А'' и конца''В'' вектора [[Image:a4-3.jpg]] перпендикуляры на ось ''ОХ''.<br> Точки ''А<sub>1</sub>'' и ''В<sub>1</sub> ''есть проекции, соответственно, начала и конца вектора [[Image:a4-3.jpg]] на эту ось.<br> '''Проекцией вектора [[Image:a4-3.jpg]] на какую-либо ось''' называется длина отрезка ''А<sub>1</sub>В<sub>1</sub> ''между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».<br> Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, ''а<sub>x</sub>'' и ''а<sub>y</sub> ''- проекции вектора на оси координат ''ОХ'' и ''ОY.''<br> Согласно определению проекции вектора на ось можно записать:<br>[[Image:a4-1.jpg|center]] Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора.<br> Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций. В противном случае (см. ''рис.1.5'') она считается отрицательной.<br> Из рисунков 1.5 и 1.6 нетрудно увидеть, что проекция вектора на ось будет положительной, когда вектор составляет острый угол с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекций тупой угол. | + | [[Image:A1.5.jpg|center|181x114px|Положение точки в пространстве]] Опустим из начала ''А'' и конца''В'' вектора [[Image:A4-3.jpg|14x21px|A4-3.jpg]] перпендикуляры на ось ''ОХ''.<br> Точки ''А<sub>1</sub>'' и ''В<sub>1</sub> ''есть проекции, соответственно, начала и конца вектора [[Image:A4-3.jpg|15x20px|A4-3.jpg]] на эту ось.<br> '''Проекцией вектора [[Image:A4-3.jpg|14x19px|A4-3.jpg]] на какую-либо ось''' называется длина отрезка ''А<sub>1</sub>В<sub>1</sub> ''между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».<br> Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, ''а<sub>x</sub>'' и ''а<sub>y</sub> ''- проекции вектора на оси координат ''ОХ'' и ''ОY.''<br> Согласно определению проекции вектора на ось можно записать:<br>[[Image:A4-1.jpg|center|134x29px|Положение точки в пространстве]] Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и [[Модуль_вектора_магнитной_индукции._Сила_Ампера|модуль вектора]].<br> Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций. В противном случае (см. ''рис.1.5'') она считается отрицательной.<br> Из рисунков 1.5 и 1.6 нетрудно увидеть, что проекция вектора на ось будет положительной, когда вектор составляет острый угол с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекций тупой угол. |
| | | | |
| - | [[Image:A1.6.jpg|center|187x120px]] Положение точки в пространстве можно задавать с помощью координат или радиус-вектора, соединяющего начало координат и точку.<br><br><br> ???<br> 1. Что называется телом отсчета?<br> 2. Какими способами можно задать положение точки?<br> 3. Как задают положение точки в пространстве с помощью координат?<br> 4. Что называется радиус-вектором?<br> 5. Что называется проекцией вектора на ось?<br> 6. Чему равна проекция вектора на ось, если вектор направлен так же, как и ось проекции?<br> 7. Чему равна проекция вектора на ось, если вектор направлен противоположно оси проекции?<br> 8. Чему равна проекция вектора на перпендикулярную к нему ось?<br> <br> | + | [[Image:A1.6.jpg|center|187x120px|Положение точки в пространстве]] Положение точки в пространстве можно задавать с помощью координат или радиус-вектора, соединяющего начало координат и точку.<br><br><br> ???<br> 1. Что называется телом отсчета?<br> 2. Какими способами можно задать положение точки?<br> 3. Как задают положение точки в пространстве с помощью координат?<br> 4. Что называется радиус-вектором?<br> 5. Что называется проекцией [[Вектор магнитной индукции. Линии магнитной индукции|вектора]] на ось?<br> 6. Чему равна проекция вектора на ось, если вектор направлен так же, как и ось проекции?<br> 7. Чему равна проекция вектора на ось, если вектор направлен противоположно оси проекции?<br> 8. Чему равна проекция вектора на перпендикулярную к нему ось?<br> <br> |
| | | | |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, [[Физика 10 класс|Физика]] 10 класс'' |
| | | | |
| | <br> | | <br> |
| Строка 22: |
Строка 22: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 12:23, 4 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Положение точки в пространстве
Чтобы решить задачу о движении тела, прежде всего надо уметь определять, или, что одно и то же, задавать, положение его в пространстве. Как же определяют положение точки?
Наблюдая за любым телом, мы замечаем, что его положение в один и тот же момент времени относительно различных тел различно. Например, космический корабль, запущенный с космодрома Байконур, занимает совершенно различные положения относительно Земли, Луны и Солнца. Поэтому в данном случае обязательно надо указать физическое тело, относительно которого задается положение данного тела или же данной точки. Такое тело называют телом отсчета.
Тело отсчета можно выбрать произвольно. Им может быть космодром, самолет, в котором мы летим, космический корабль, Земля, Солнце, звезды и т. д. Но относительно различных точек тела отсчета положение любого другого тела или точки тоже различно. Если, например, за тело отсчета принять Землю, то положение спутника Земли относительно Москвы будет иным, нежели относительно космодрома Байконур. Строго говоря, мы должны указать, относительно какой точки выбранного тела отсчета задается положение данной точки или тела.
Если тело отсчета выбрано, то относительно него положение точки можно задать с помощью координат или радиус-вектора. Выбор системы отсчета и системы координат должен быть разумным, чтобы описание движения тела выглядело достаточно просто, но в то же время мы могли бы ответить на все вопросы задачи.
Рассмотрим эти два способа задания положения точки.
Задание положения точки с помощью координат. Из курса математики вы знаете, что положение точки на плоскости можно задать с помощью двух чисел, которые называются координатами этой точки. Для этого, как известно, можно на плоскости провести две пересекающиеся взаимно перпендикулярные оси, например оси ОХ и ОY. Точку пересечения осей называют началом координат, а сами оси - координатными осями.
Координаты точки М1 (рис.1.2) равны x1 = 2,у1 = 4; координаты точки М2 равны х2 = -2,5, у2 = -3,5.
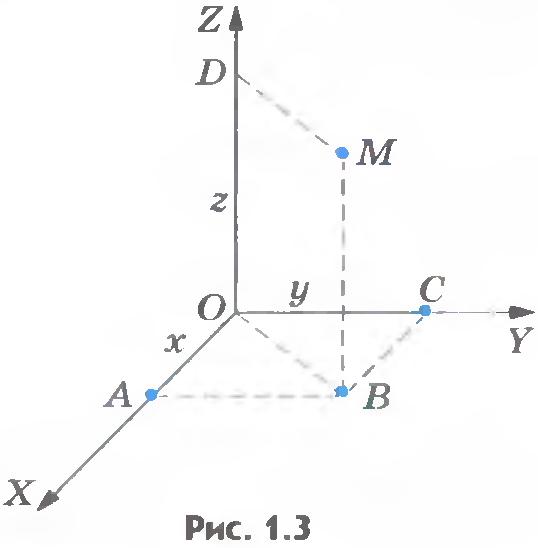
Положение точки М в пространстве относительно тела отсчета можно задать с помощью трех координат. Чтобы это сделать, необходимо через выбранную точку тела отсчета провести три взаимно перпендикулярные оси ОХ, ОY, 0Z. В полученной системе координат положение точки будет определяться тремя координатами х, у, z.
Если число х положительно, то отрезок откладывается в положительном направлении оси ОХ (рис.1.3) (x = ОА). Если же число х отрицательно, то отрезок откладывается в отрицательном направлении оси ОХ. Из конца этого отрезка проводят прямую, параллельную оси ОY, и на этой прямой откладывают отрезок от оси ОХ, соответствующий числу у (у = АВ) - в положительном направлении оси ОY, если число у положительно, и в отрицательном направлении оси ОY, если число у отрицательно.
Далее из точки В другого отрезка проводят прямую, параллельную оси ОZ. На этой прямой от координатной плоскости ХОY откладывают отрезок, соответствующий числу z. Направление, в котором откладывают этот отрезок, определяют так же, как и в предыдущих случаях.
Конец третьего отрезка и есть та точка, положение которой задается координатами х, у, z.
Чтобы определить координаты данной точки, необходимо провести в обратной последовательности те операции, которые мы осуществляли, находя положение этой точки по ее координатам.
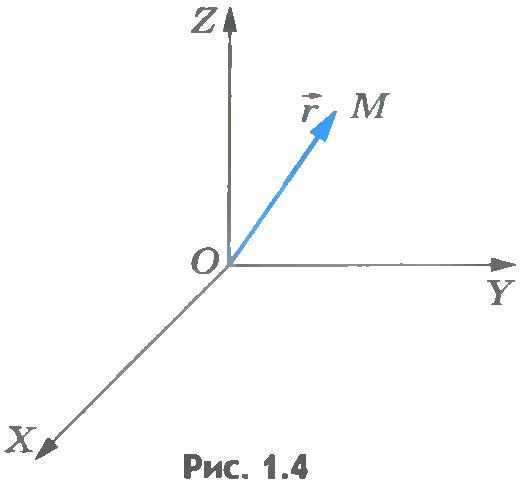
Задание положения точки с помощью радиус-вектора. Положение точки можно задать не только с помощью координат, но и с помощью радиус-вектора. Радиус-вектор - это направленный отрезок, проведенный из начала координат в данную точку.
Радиус-вектор принято обозначать буквой 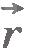 . Длина радиус-вектора, или, что одно и то же, его модуль (рис.1.4), есть расстояние от начала координат до точки М.
Положение точки будет определено с помощью радиус-вектора только в том случае, если известны его модуль (длина) и направление в пространстве. Лишь при этом условии мы будем знать, в каком направлении от начала координат следует отложить отрезок длиной r, чтобы определить положение точки. . Длина радиус-вектора, или, что одно и то же, его модуль (рис.1.4), есть расстояние от начала координат до точки М.
Положение точки будет определено с помощью радиус-вектора только в том случае, если известны его модуль (длина) и направление в пространстве. Лишь при этом условии мы будем знать, в каком направлении от начала координат следует отложить отрезок длиной r, чтобы определить положение точки.
Итак, положение точки в пространстве определяется ее координатами или ее радиус-вектором.
Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось?
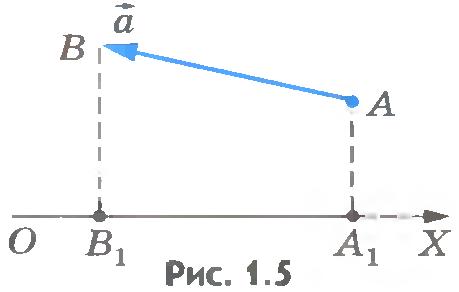
Изобразим какую-либо ось (рис.1.5), например ось ОХ.
Опустим из начала А и концаВ вектора 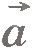 перпендикуляры на ось ОХ. перпендикуляры на ось ОХ.
Точки А1 и В1 есть проекции, соответственно, начала и конца вектора 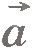 на эту ось. на эту ось.
Проекцией вектора 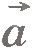 на какую-либо ось называется длина отрезка А1В1 между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-». на какую-либо ось называется длина отрезка А1В1 между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, аx и аy - проекции вектора на оси координат ОХ и ОY.
Согласно определению проекции вектора на ось можно записать:
Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора.
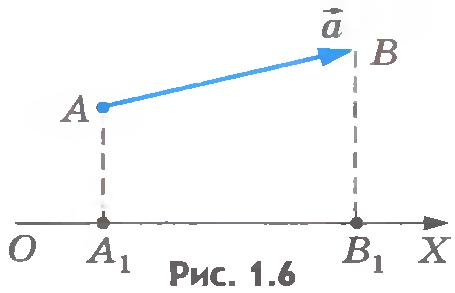
Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций. В противном случае (см. рис.1.5) она считается отрицательной.
Из рисунков 1.5 и 1.6 нетрудно увидеть, что проекция вектора на ось будет положительной, когда вектор составляет острый угол с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекций тупой угол.
Положение точки в пространстве можно задавать с помощью координат или радиус-вектора, соединяющего начало координат и точку.
???
1. Что называется телом отсчета?
2. Какими способами можно задать положение точки?
3. Как задают положение точки в пространстве с помощью координат?
4. Что называется радиус-вектором?
5. Что называется проекцией вектора на ось?
6. Чему равна проекция вектора на ось, если вектор направлен так же, как и ось проекции?
7. Чему равна проекция вектора на ось, если вектор направлен противоположно оси проекции?
8. Чему равна проекция вектора на перпендикулярную к нему ось?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Материалы по физике, задание и ответы по классам, планы конспектов уроков по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|