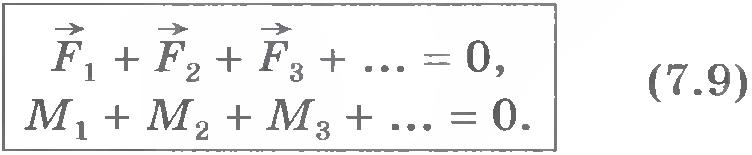|
|
|
| (1 промежуточная версия не показана) | | Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Второе условие, равновесия твердого тела</metakeywords> | | <metakeywords>Физика, 10 класс, Второе условие, равновесия твердого тела</metakeywords> |
| | | | |
| - | Равенство нулю суммы внешних сил, действующих на твердое тело, необходимо для его равновесия, но недостаточно. В этом легко убедиться. Приложите к доске, лежащей на столе, в различных точках две равные по модулю и противоположно направленные силы так, как показано на рисунке 7.2. <br>[[Image:a7.2.jpg|center]]Сумма этих сил равна нулю: [[Image:a54-8.jpg]]. Но доска, тем не менее, будет поворачиваться. Точно так же две одинаковые по модулю и противоположно направленные силы поворачивают руль велосипеда или автомобиля (''рис.7.3''). Почему так происходит, понять нетрудно. Ведь любое тело находится в равновесии, когда сумма всех сил, действующих на каждый его элемент, равна нулю. Но если сумма внешних сил равна нулю, то сумма всех сил, приложенных к каждому элементу тела, может быть не равна нулю. В этом случае тело не будет находиться в равновесии. В рассмотренных примерах доска и руль потому и не находятся в равновесии, что сумма всех сил, действующих на отдельные элементы этих тел, не равна нулю.<br>[[Image:a7.3.jpg|center]] Выясним, какое же еще условие для внешних сил, кроме равенства нулю их суммы, должно выполняться, чтобы твердое тело находилось в равновесии. Для этого воспользуемся теоремой об изменении кинетической энергии.<br> Найдем, например, условие равновесия стержня, шарнирно закрепленного на горизонтальной оси в точке О (''рис.7.4''). Это простое устройство, как вам известно из курса физики 7 класса, представляет собой рычаг. Пусть к рычагу приложены перпендикулярно стержню силы [[Image:a54-9.jpg]] и [[Image:a54-10.jpg]]. В частности, это могут быть силы натяжения нитей, к концам которых прикреплены грузы. Кроме сил [[Image:a54-9.jpg]] и [[Image:a54-10.jpg]] на рычаг действует направленная вертикально вверх сила реакции [[Image:a54-11.jpg]] со стороны оси рычага. При равновесии рычага сумма всех трех сил равна нулю: [[Image:a54-12.jpg]].<br>[[Image:a7.4.jpg|center]] Вычислим работу, которую совершают внешние силы при повороте рычага на очень малый угол [[Image:a54-13.jpg]]. Точки приложения сил [[Image:a54-9.jpg]] и [[Image:a54-10.jpg]] пройдут пути ''s<sub>1</sub>=BB<sub>1</sub>'' и ''s<sub>2</sub>=CC<sub>1</sub>'' (дуги ''BB<sub>1</sub>'' и ''CC<sub>1</sub>'' при малых углах [[Image:a54-13.jpg]] можно считать прямолинейными отрезками). Работа''A<sub>1</sub>=F<sub>1</sub>s<sub>1</sub> ''силы [[Image:a54-9.jpg]] положительна, потому что точка ''B'' перемещается по направлению действия силы, а работа ''A<sub>2</sub>=-F<sub>2</sub>s<sub>2</sub>''<sub></sub>силы [[Image:a54-10.jpg]] отрицательна, поскольку точка ''C'' движется в сторону, противоположную направлению силы [[Image:a54-10.jpg]]. Сила [[Image:a54-11.jpg]] работы не совершает, так как точка ее приложения не перемещается.<br> Пройденные пути ''s<sub>1</sub> ''и ''s<sub>2</sub>'' можно выразить через угол поворота рычага [[Image:a54-13.jpg]], измеренный в радианах: [[Image:a54-14.jpg]] и [[Image:a54-15.jpg]].<br> Учитывая это, перепишем выражения для работы так:<br>[[Image:a54-1.jpg|center]] Радиусы''ВО'' и''СО'' дуг окружностей, описываемых точками приложения сил [[Image:a54-9.jpg]] и [[Image:a54-10.jpg]], являются перпендикулярами, опущенными из оси вращения на линии действия этих сил.<br> Кратчайшее расстояние от оси вращения до линии действия силы называют '''плечом силы'''.<br> Будем обозначать плечо силы буквой ''d''. Тогда [[Image:a54-16.jpg]] - плечо силы [[Image:a54-9.jpg]], а [[Image:a54-17.jpg]] - плечо силы [[Image:a54-10.jpg]]. При этом выражения (7.4) примут вид<br>[[Image:a54-2.jpg|center]] Из формул (7.5) видно, что при заданном угле поворота тела (стержня) работа каждой приложенной к этому телу силы равна произведению модуля силы на плечо взятому со знаком «+» или «-». Это произведение будем называть '''моментом силы.'''<br> '''Моментом силы относительно оси вращения тела''' называется произведение модуля силы на ее плечо. Момент силы может быть положительным или отрицательным.<br> Момент силы [[Image:a37-4.jpg|14x21px]] обозначим буквой ''M'':<br>[[Image:a54-3.jpg|center]] Будем считать момент силы [[Image:a37-4.jpg|15x23px]] ''положительным'', если она стремится повернуть тело против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда момент силы [[Image:a54-9.jpg]] равен ''M<sub>1</sub>=F<sub>1</sub>d<sub>1</sub> ''(см. рис. 7.4), а момент силы [[Image:a54-10.jpg]] равен ''M<sub>2</sub>=-F<sub>2</sub>d<sub>2</sub>''. Следовательно, выражения (7.5) для работы можно переписать в виде<br>[[Image:a54-4.jpg|center]]а полную работу внешних сил выразить формулой:<br>[[Image:a54-5.jpg|center]] Когда тело приходит в движение, его кинетическая энергия увеличивается. Для увеличения кинетической энергии внешние силы должны совершить работу. Согласно уравнению (7.7) ненулевая работа может быть совершена лишь в том случае, если суммарный момент внешних сил отличен от нуля. Если же суммарный момент внешних сил, действующих на тело, равен нулю, то работа не совершается и кинетическая энергия тела не увеличивается (остается равной нулю), следовательно, тело не приходит в движение. Равенство<br>[[Image:a54-6.jpg|center]]и есть второе условие, необходимое для равновесия твердого тела.<br> '''При равновесии твердого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю.''' Итак, в случае произвольного числа внешних сил условия равновесия абсолютно твердого тела следующие:<br>[[Image:a54-7.jpg|center]] Если же тело не абсолютно твердое, то под действием приложенных к нему внешних сил оно может и не оставаться в равновесии, хотя сумма внешних сил и сумма их моментов относительно любой оси равна нулю. Это происходит потому, что под действием внешних сил тело может деформироваться и сумма всех сил, действующих на каждый его элемент, в этом случае не будет равна нулю.<br> Приложим, например, к концам резинового шнура две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур не будет находиться в равновесии (шнур растягивается), хотя сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.<br> Условия (7.9) являются необходимыми и достаточными для равновесия твердого тела. Если они выполняются, то твердое тело находится в равновесии, так как сумма сил, действующих на каждый элемент этого тела, равна нулю.<br><br><br> ???<br> 1. Что называется моментом силы?<br> 2. Какие условия необходимы и достаточны для равновесия твердого тела?<br>
| + | Равенство нулю суммы внешних сил, действующих на твердое тело, необходимо для его равновесия, но недостаточно. В этом легко убедиться. Приложите к доске, лежащей на столе, в различных точках две равные по модулю и противоположно направленные силы так, как показано на рисунке 7.2. <br>[[Image:A7.2.jpg|center|181x167px|равновесие твердого тела]]Сумма этих сил равна нулю: [[Image:A54-8.jpg|86x20px|A54-8.jpg]]. Но доска, тем не менее, будет поворачиваться. Точно так же две одинаковые по модулю и противоположно направленные силы поворачивают руль велосипеда или автомобиля (''рис.7.3''). Почему так происходит, понять нетрудно. Ведь любое тело находится в равновесии, когда сумма всех сил, действующих на каждый его элемент, равна нулю. Но если сумма внешних сил равна нулю, то сумма всех сил, приложенных к каждому элементу тела, может быть не равна нулю. В этом случае тело не будет находиться в равновесии. В рассмотренных примерах доска и руль потому и не находятся в [[Обратимость_химических_реакций._Химическое_равновесие|равновесии]], что сумма всех сил, действующих на отдельные элементы этих тел, не равна нулю.<br>[[Image:A7.3.jpg|center|168x172px|равновесие твердого тела]] Выясним, какое же еще условие для внешних сил, кроме равенства нулю их суммы, должно выполняться, чтобы твердое тело находилось в равновесии. Для этого воспользуемся теоремой об изменении кинетической энергии.<br> Найдем, например, условие равновесия стержня, шарнирно закрепленного на горизонтальной оси в точке О (''рис.7.4''). Это простое устройство, как вам известно из курса [[Физика_7_класс|физики 7 класса]], представляет собой рычаг. Пусть к рычагу приложены перпендикулярно стержню силы [[Image:A54-9.jpg|21x28px|A54-9.jpg]] и [[Image:A54-10.jpg|23x29px|A54-10.jpg]]. В частности, это могут быть силы натяжения нитей, к концам которых прикреплены грузы. Кроме сил [[Image:A54-9.jpg|21x28px|A54-9.jpg]] и [[Image:A54-10.jpg|23x30px|A54-10.jpg]] на рычаг действует направленная вертикально вверх сила реакции [[Image:A54-11.jpg|23x28px|A54-11.jpg]] со стороны оси рычага. При равновесии рычага сумма всех трех сил равна нулю: [[Image:A54-12.jpg|center|140x26px|A54-12.jpg]].<br>[[Image:A7.4.jpg|center|222x118px|равновесие твердого тела]] Вычислим работу, которую совершают внешние силы при повороте рычага на очень малый угол [[Image:A54-13.jpg|16x14px|A54-13.jpg]]. Точки приложения сил [[Image:A54-9.jpg|19x25px|A54-9.jpg]] и [[Image:A54-10.jpg|22x29px|A54-10.jpg]] пройдут пути ''s<sub>1</sub>=BB<sub>1</sub>'' и ''s<sub>2</sub>=CC<sub>1</sub>'' (дуги ''BB<sub>1</sub>'' и ''CC<sub>1</sub>'' при малых углах [[Image:A54-13.jpg|15x13px|A54-13.jpg]] можно считать прямолинейными отрезками). Работа''A<sub>1</sub>=F<sub>1</sub>s<sub>1</sub> ''силы [[Image:A54-9.jpg|21x27px|A54-9.jpg]] положительна, потому что точка ''B'' перемещается по направлению действия силы, а работа ''A<sub>2</sub>=-F<sub>2</sub>s<sub>2</sub>''силы [[Image:A54-10.jpg|22x28px|A54-10.jpg]] отрицательна, поскольку точка ''C'' движется в сторону, противоположную направлению силы [[Image:A54-10.jpg|19x25px|A54-10.jpg]]. Сила [[Image:A54-11.jpg|20x24px|A54-11.jpg]] работы не совершает, так как точка ее приложения не перемещается.<br> Пройденные пути ''s<sub>1</sub> ''и ''s<sub>2</sub>'' можно выразить через угол поворота рычага [[Image:A54-13.jpg|17x14px|A54-13.jpg]], измеренный в радианах: [[Image:A54-14.jpg|99x19px|A54-14.jpg]] и [[Image:A54-15.jpg|96x19px|A54-15.jpg]].<br> Учитывая это, перепишем выражения для работы так:<br>[[Image:A54-1.jpg|center|201x40px|равновесие твердого тела]] Радиусы''ВО'' и''СО'' дуг окружностей, описываемых точками приложения сил [[Image:A54-9.jpg|19x25px|A54-9.jpg]] и [[Image:A54-10.jpg|22x28px|A54-10.jpg]], являются перпендикулярами, опущенными из оси вращения на линии действия этих сил.<br> Кратчайшее расстояние от оси вращения до линии действия силы называют '''плечом силы'''.<br> Будем обозначать плечо силы буквой ''d''. Тогда [[Image:A54-16.jpg|83x19px|A54-16.jpg]] - плечо силы [[Image:A54-9.jpg|18x24px|A54-9.jpg]], а [[Image:A54-17.jpg|80x19px|A54-17.jpg]] - плечо силы [[Image:A54-10.jpg|18x24px|A54-10.jpg]]. При этом выражения (7.4) примут вид<br>[[Image:A54-2.jpg|center|187x43px|равновесие твердого тела]] Из формул (7.5) видно, что при заданном угле поворота тела (стержня) работа каждой приложенной к этому телу силы равна произведению модуля силы на плечо взятому со знаком «+» или «-». Это произведение будем называть '''моментом [[Архимедовая_сила|силы]].'''<br> '''Моментом силы относительно оси вращения тела''' называется произведение модуля силы на ее плечо. Момент силы может быть положительным или отрицательным.<br> Момент силы [[Image:A37-4.jpg|14x21px|A37-4.jpg]] обозначим буквой ''M'':<br>[[Image:A54-3.jpg|center|126x40px|равновесие твердого тела]] Будем считать момент силы [[Image:A37-4.jpg|15x23px|A37-4.jpg]] ''положительным'', если она стремится повернуть тело против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда момент силы [[Image:A54-9.jpg|20x26px|A54-9.jpg]] равен ''M<sub>1</sub>=F<sub>1</sub>d<sub>1</sub> ''(см. рис. 7.4), а момент силы [[Image:A54-10.jpg|18x24px|A54-10.jpg]] равен ''M<sub>2</sub>=-F<sub>2</sub>d<sub>2</sub>''. Следовательно, выражения (7.5) для работы можно переписать в виде<br>[[Image:A54-4.jpg|center|173x46px|равновесие твердого тела]]а полную работу внешних сил выразить формулой:<br>[[Image:A54-5.jpg|center|353x23px|равновесие твердого тела]] Когда тело приходит в движение, его [[Кинетическая_энергия_и_ее_изменение|кинетическая энергия]] увеличивается. Для увеличения кинетической энергии внешние силы должны совершить работу. Согласно уравнению (7.7) ненулевая работа может быть совершена лишь в том случае, если суммарный момент внешних сил отличен от нуля. Если же суммарный момент внешних сил, действующих на тело, равен нулю, то работа не совершается и кинетическая энергия тела не увеличивается (остается равной нулю), следовательно, тело не приходит в движение. Равенство<br>[[Image:A54-6.jpg|center|199x20px|равновесие твердого тела]]и есть второе условие, необходимое для равновесия твердого тела.<br> '''При ''' '''[[Равновесие_тел|равновесии]]''' '''твердого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю.''' Итак, в случае произвольного числа внешних сил условия равновесия абсолютно твердого тела следующие:<br>[[Image:A54-7.jpg|center|307x63px|равновесие твердого тела]] Если же тело не абсолютно твердое, то под действием приложенных к нему внешних сил оно может и не оставаться в равновесии, хотя сумма внешних сил и сумма их моментов относительно любой оси равна нулю. Это происходит потому, что под действием внешних [[Інтерактивна_вправа_до_уроку_на_тему_«"Сильніше_за_силу"_(казка)._Прислів'я._Підсумок_за_темою»|сил]] тело может деформироваться и сумма всех сил, действующих на каждый его элемент, в этом случае не будет равна нулю.<br> Приложим, например, к концам резинового шнура две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур не будет находиться в равновесии (шнур растягивается), хотя сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.<br> Условия (7.9) являются необходимыми и достаточными для равновесия твердого тела. Если они выполняются, то твердое тело находится в равновесии, так как сумма сил, действующих на каждый элемент этого тела, равна нулю.<br><br><br> ???<br> 1. Что называется моментом силы?<br> 2. Какие условия необходимы и достаточны для равновесия твердого тела?<br> <br> |
| - | <br>
| + | |
| | | | |
| | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| Строка 13: |
Строка 12: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 05:18, 5 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Второе условие равновесия твердого тела
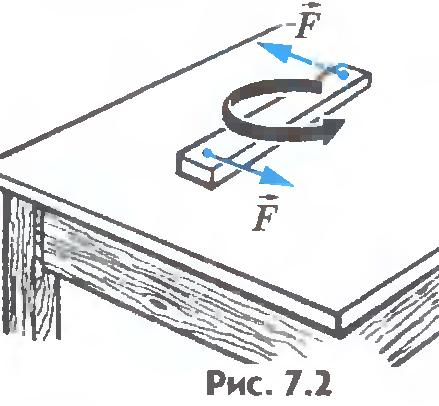
Равенство нулю суммы внешних сил, действующих на твердое тело, необходимо для его равновесия, но недостаточно. В этом легко убедиться. Приложите к доске, лежащей на столе, в различных точках две равные по модулю и противоположно направленные силы так, как показано на рисунке 7.2.
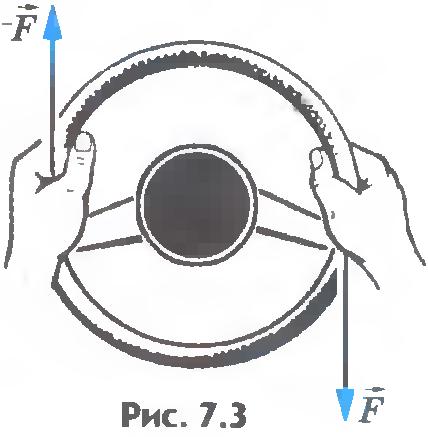
Сумма этих сил равна нулю:  . Но доска, тем не менее, будет поворачиваться. Точно так же две одинаковые по модулю и противоположно направленные силы поворачивают руль велосипеда или автомобиля (рис.7.3). Почему так происходит, понять нетрудно. Ведь любое тело находится в равновесии, когда сумма всех сил, действующих на каждый его элемент, равна нулю. Но если сумма внешних сил равна нулю, то сумма всех сил, приложенных к каждому элементу тела, может быть не равна нулю. В этом случае тело не будет находиться в равновесии. В рассмотренных примерах доска и руль потому и не находятся в равновесии, что сумма всех сил, действующих на отдельные элементы этих тел, не равна нулю. . Но доска, тем не менее, будет поворачиваться. Точно так же две одинаковые по модулю и противоположно направленные силы поворачивают руль велосипеда или автомобиля (рис.7.3). Почему так происходит, понять нетрудно. Ведь любое тело находится в равновесии, когда сумма всех сил, действующих на каждый его элемент, равна нулю. Но если сумма внешних сил равна нулю, то сумма всех сил, приложенных к каждому элементу тела, может быть не равна нулю. В этом случае тело не будет находиться в равновесии. В рассмотренных примерах доска и руль потому и не находятся в равновесии, что сумма всех сил, действующих на отдельные элементы этих тел, не равна нулю.
Выясним, какое же еще условие для внешних сил, кроме равенства нулю их суммы, должно выполняться, чтобы твердое тело находилось в равновесии. Для этого воспользуемся теоремой об изменении кинетической энергии.
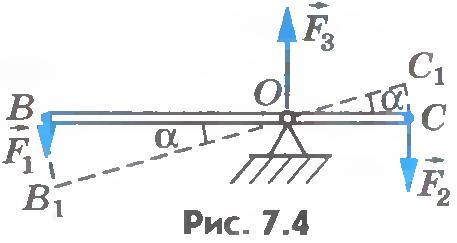
Найдем, например, условие равновесия стержня, шарнирно закрепленного на горизонтальной оси в точке О (рис.7.4). Это простое устройство, как вам известно из курса физики 7 класса, представляет собой рычаг. Пусть к рычагу приложены перпендикулярно стержню силы 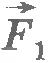 и и  . В частности, это могут быть силы натяжения нитей, к концам которых прикреплены грузы. Кроме сил . В частности, это могут быть силы натяжения нитей, к концам которых прикреплены грузы. Кроме сил 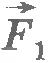 и и 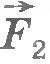 на рычаг действует направленная вертикально вверх сила реакции на рычаг действует направленная вертикально вверх сила реакции 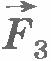 со стороны оси рычага. При равновесии рычага сумма всех трех сил равна нулю: . со стороны оси рычага. При равновесии рычага сумма всех трех сил равна нулю: .
Вычислим работу, которую совершают внешние силы при повороте рычага на очень малый угол 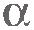 . Точки приложения сил . Точки приложения сил 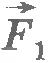 и и 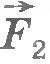 пройдут пути s1=BB1 и s2=CC1 (дуги BB1 и CC1 при малых углах пройдут пути s1=BB1 и s2=CC1 (дуги BB1 и CC1 при малых углах 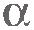 можно считать прямолинейными отрезками). РаботаA1=F1s1 силы можно считать прямолинейными отрезками). РаботаA1=F1s1 силы 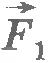 положительна, потому что точка B перемещается по направлению действия силы, а работа A2=-F2s2силы положительна, потому что точка B перемещается по направлению действия силы, а работа A2=-F2s2силы 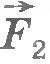 отрицательна, поскольку точка C движется в сторону, противоположную направлению силы отрицательна, поскольку точка C движется в сторону, противоположную направлению силы 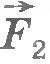 . Сила . Сила 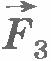 работы не совершает, так как точка ее приложения не перемещается. работы не совершает, так как точка ее приложения не перемещается.
Пройденные пути s1 и s2 можно выразить через угол поворота рычага 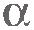 , измеренный в радианах: , измеренный в радианах: 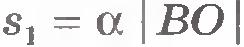 и и  . .
Учитывая это, перепишем выражения для работы так:
РадиусыВО иСО дуг окружностей, описываемых точками приложения сил 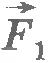 и и 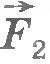 , являются перпендикулярами, опущенными из оси вращения на линии действия этих сил. , являются перпендикулярами, опущенными из оси вращения на линии действия этих сил.
Кратчайшее расстояние от оси вращения до линии действия силы называют плечом силы.
Будем обозначать плечо силы буквой d. Тогда 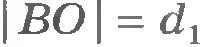 - плечо силы - плечо силы 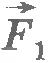 , а , а 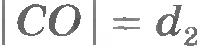 - плечо силы - плечо силы 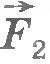 . При этом выражения (7.4) примут вид . При этом выражения (7.4) примут вид
Из формул (7.5) видно, что при заданном угле поворота тела (стержня) работа каждой приложенной к этому телу силы равна произведению модуля силы на плечо взятому со знаком «+» или «-». Это произведение будем называть моментом силы.
Моментом силы относительно оси вращения тела называется произведение модуля силы на ее плечо. Момент силы может быть положительным или отрицательным.
Момент силы 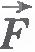 обозначим буквой M: обозначим буквой M:
Будем считать момент силы 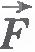 положительным, если она стремится повернуть тело против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда момент силы положительным, если она стремится повернуть тело против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда момент силы 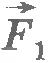 равен M1=F1d1 (см. рис. 7.4), а момент силы равен M1=F1d1 (см. рис. 7.4), а момент силы 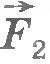 равен M2=-F2d2. Следовательно, выражения (7.5) для работы можно переписать в виде равен M2=-F2d2. Следовательно, выражения (7.5) для работы можно переписать в виде
а полную работу внешних сил выразить формулой:
Когда тело приходит в движение, его кинетическая энергия увеличивается. Для увеличения кинетической энергии внешние силы должны совершить работу. Согласно уравнению (7.7) ненулевая работа может быть совершена лишь в том случае, если суммарный момент внешних сил отличен от нуля. Если же суммарный момент внешних сил, действующих на тело, равен нулю, то работа не совершается и кинетическая энергия тела не увеличивается (остается равной нулю), следовательно, тело не приходит в движение. Равенство
и есть второе условие, необходимое для равновесия твердого тела.
При равновесии твердого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю. Итак, в случае произвольного числа внешних сил условия равновесия абсолютно твердого тела следующие:
Если же тело не абсолютно твердое, то под действием приложенных к нему внешних сил оно может и не оставаться в равновесии, хотя сумма внешних сил и сумма их моментов относительно любой оси равна нулю. Это происходит потому, что под действием внешних сил тело может деформироваться и сумма всех сил, действующих на каждый его элемент, в этом случае не будет равна нулю.
Приложим, например, к концам резинового шнура две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур не будет находиться в равновесии (шнур растягивается), хотя сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.
Условия (7.9) являются необходимыми и достаточными для равновесия твердого тела. Если они выполняются, то твердое тело находится в равновесии, так как сумма сил, действующих на каждый элемент этого тела, равна нулю.
???
1. Что называется моментом силы?
2. Какие условия необходимы и достаточны для равновесия твердого тела?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирование уроков по физике, ответы на тесты, задания и ответы по классам, домашнее задание и работа по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|