|
|
|
| (1 промежуточная версия не показана) | | Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Основное уравнение, молекулярно-кинетической, теории газов</metakeywords> | | <metakeywords>Физика, 10 класс, Основное уравнение, молекулярно-кинетической, теории газов</metakeywords> |
| | | | |
| - | Приступаем к выводу основного уравнения молекулярно-кинетической теории газов. В этом уравнении устанавливается зависимость давления газа от средней кинетической энергии его молекул. После вывода этого уравнения в XIX в. и экспериментального доказательства его справедливости началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.<br> Доказательство почти любого утверждения в физике, вывод любого уравнения могут быть проделаны с различной степенью строгости и убедительности: очень упрощенно, более или менее строго или же с полной строгостью, доступной современной науке.<br> Строгий вывод уравнения молекулярно-кинетической теории газов довольно сложен. Поэтому мы ограничимся сильно упрощенным, схематичным выводом уравнения. Несмотря на все упрощения, результат получится верный.<br> '''Вывод основного уравнения.''' Вычислим давление газа на стенку''CD'' сосуда ''ABCD'' площадью ''S'', перпендикулярную координатной оси ''OX'' (''рис.8.13'').<br>[[Image:A8.13.jpg|center]] При ударе молекулы о стенку ее импульс изменяется: [[Image:A63-1.jpg]]. Так как модуль скорости молекул при ударе не меняется, то [[Image:A63-2.jpg]]. Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен [[Image:A63-3.jpg]].<br> Молекул много, и каждая из них передает стенке при столкновении такой же импульс. За секунду они передадут стенке импульс [[Image:A63-4.jpg]], где ''Z'' - число столкновений всех молекул со стенкой за это время. Число очевидно, прямо пропорционально концентрации молекул, т. е. числу молекул в единице объема. Кроме того, число ''Z'' пропорционально скорости молекул [[Image:A63-15.jpg]]. Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой. Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки ''S'': [[Image:A635.jpg]]. Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с [[Image:A63-6.jpg]] и полный импульс, переданный стенке за 1 с, равен:<br>[[Image:A63-7.jpg|center]] Согласно второму закону Ньютона изменение импульса любого тела за единицу времени равно действующей на него силе: [[Image:A63-8.jpg]].<br> Учтем, что не все молекулы имеют одно и то же значение квадрата скорости [[Image:A63-16.jpg]]. В действительности средняя за секунду сила, действующая на стенку, пропорциональна не [[Image:A63-16.jpg]], а среднему квадрату скорости [[Image:A63-17.jpg]]: [[Image:A63-9.jpg]]. Так как согласно формуле (8.13) [[Image:A63-10.jpg]], то [[Image:A63-11.jpg]]. Таким образом, давление газа на стенку сосуда равно:<br>[[Image:A63-12.jpg|center]] Это и есть основное уравнение молекулярно-кинетической теории газов.<br> Формула (8.14) связывает макроскопическую величину - давление, которое может быть измерено манометром, - с микроскопическими величинами, характеризующими молекулы: их массой, скоростью хаотичного движения.<br> '''Связь давления со средней кинетической энергией молекул.''' Если через [[Image:A63-18.jpg]] обозначить среднюю кинетическую энергию поступательного движения молекулы [[Image:A63-13.jpg]], то уравнение (8.14) можно записать в виде<br>[[Image:A63-14.jpg|center]] '''''Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.'''''<br> В главе 9 докажем, что средняя кинетическая энергия молекул связана также и с температурой газа.<br> Нам удалось вычислить давление идеального газа на стенки сосуда.<br> Оно зависит от концентрации молекул. Кроме того, и это главное, давление газа пропорционально средней кинетической энергии молекул.<br><br><br> ???<br> 1. Почему молекула при соударении со стенкой действует на нее с силой, пропорциональной скорости, а давление пропорционально квадрату скорости молекулы?<br> 2. Почему и как в основном уравнении молекулярно-кинетической теории появляется множитель 1/3?<br> 3. Как средняя кинетическая энергия молекул зависит от концентрации газа и его давления на стенки сосуда?<br> | + | Приступаем к выводу основного уравнения молекулярно-кинетической теории газов. В этом уравнении устанавливается зависимость давления газа от средней [[Абсолютная_температура._Температура_—_мера_средней_кинетической_энергии_молекул|кинетической энергии]] его молекул. После вывода этого уравнения в XIX в. и экспериментального доказательства его справедливости началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.<br> Доказательство почти любого утверждения в [[Примеры_задач_по_физике_11_класс|физике]], вывод любого уравнения могут быть проделаны с различной степенью строгости и убедительности: очень упрощенно, более или менее строго или же с полной строгостью, доступной современной науке.<br> Строгий вывод уравнения молекулярно-кинетической теории газов довольно сложен. Поэтому мы ограничимся сильно упрощенным, схематичным выводом уравнения. Несмотря на все упрощения, результат получится верный.<br> '''Вывод основного уравнения.''' Вычислим давление газа на стенку''CD'' сосуда ''ABCD'' площадью ''S'', перпендикулярную координатной оси ''OX'' (''рис.8.13'').<br>[[Image:A8.13.jpg|center|209x179px|уравнение молекулярно-кинетической теории газов]] При ударе молекулы о стенку ее импульс изменяется: [[Image:A63-1.jpg|166x20px|A63-1.jpg]]. Так как модуль скорости молекул при ударе не меняется, то [[Image:A63-2.jpg|118x20px|A63-2.jpg]]. Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен [[Image:A63-3.jpg|83x21px|A63-3.jpg]].<br> Молекул много, и каждая из них передает стенке при столкновении такой же импульс. За секунду они передадут стенке импульс [[Image:A63-4.jpg|105x21px|A63-4.jpg]], где ''Z'' - число столкновений всех молекул со стенкой за это время. Число очевидно, прямо пропорционально концентрации молекул, т. е. числу молекул в единице объема. Кроме того, число ''Z'' пропорционально скорости молекул [[Image:A63-15.jpg|37x21px|A63-15.jpg]]. Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой. Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки ''S'': [[Image:A635.jpg|110x20px|A635.jpg]]. Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с [[Image:A63-6.jpg|133x36px|A63-6.jpg]] и полный [[Импульс_тела|импульс]], переданный стенке за 1 с, равен:<br>[[Image:A63-7.jpg|center|208x26px|уравнение молекулярно-кинетической теории газов]] Согласно [[Второй_закон_Ньютона|второму закону Ньютона]] изменение импульса любого тела за единицу времени равно действующей на него силе: [[Image:A63-8.jpg|118x21px|A63-8.jpg]].<br> Учтем, что не все молекулы имеют одно и то же значение квадрата скорости [[Image:A63-16.jpg|22x22px|A63-16.jpg]]. В действительности средняя за секунду сила, действующая на стенку, пропорциональна не [[Image:A63-16.jpg|22x22px|A63-16.jpg]], а среднему квадрату скорости [[Image:A63-17.jpg|23x28px|A63-17.jpg]]: [[Image:A63-9.jpg|114x26px|A63-9.jpg]]. Так как согласно формуле (8.13) [[Image:A63-10.jpg|89x39px|A63-10.jpg]], то [[Image:A63-11.jpg|134x35px|A63-11.jpg]]. Таким образом, давление газа на стенку сосуда равно:<br>[[Image:A63-12.jpg|center|267x41px|уравнение молекулярно-кинетической теории газов]] Это и есть основное уравнение молекулярно-кинетической теории газов.<br> Формула (8.14) связывает макроскопическую величину - давление, которое может быть измерено манометром, - с микроскопическими величинами, характеризующими молекулы: их массой, скоростью хаотичного движения.<br> '''Связь давления со средней кинетической энергией молекул.''' Если через [[Image:A63-18.jpg|18x21px|A63-18.jpg]] обозначить среднюю кинетическую энергию поступательного движения молекулы [[Image:A63-13.jpg|98x43px|A63-13.jpg]]то уравнение (8.14) можно записать в виде<br>[[Image:A63-14.jpg|center|193x47px|уравнение молекулярно-кинетической теории газов]] '''''Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного [[Видимые_движения_небесных_тел|движения]] молекул.'''''<br> В главе 9 докажем, что средняя кинетическая энергия молекул связана также и с температурой газа.<br> Нам удалось вычислить давление идеального газа на стенки сосуда.<br> Оно зависит от концентрации молекул. Кроме того, и это главное, давление газа пропорционально средней кинетической энергии молекул.<br><br><br> ???<br> 1. Почему молекула при соударении со стенкой действует на нее с силой, пропорциональной скорости, а давление пропорционально квадрату скорости молекулы?<br> 2. Почему и как в основном уравнении молекулярно-кинетической теории появляется множитель 1/3?<br> 3. Как средняя кинетическая энергия молекул зависит от концентрации газа и его давления на стенки сосуда?<br> |
| | | | |
| - | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, [[Физика,_химия,_космология|Физика]] 10 класс'' |
| | | | |
| | <br> <sub>Планирования [[Физика и астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Планирования [[Физика и астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика 10 класс|по физике для 10 класса]]</sub> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 09:50, 5 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Основное уравнение молекулярно-кинетической теории газов
Приступаем к выводу основного уравнения молекулярно-кинетической теории газов. В этом уравнении устанавливается зависимость давления газа от средней кинетической энергии его молекул. После вывода этого уравнения в XIX в. и экспериментального доказательства его справедливости началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.
Доказательство почти любого утверждения в физике, вывод любого уравнения могут быть проделаны с различной степенью строгости и убедительности: очень упрощенно, более или менее строго или же с полной строгостью, доступной современной науке.
Строгий вывод уравнения молекулярно-кинетической теории газов довольно сложен. Поэтому мы ограничимся сильно упрощенным, схематичным выводом уравнения. Несмотря на все упрощения, результат получится верный.
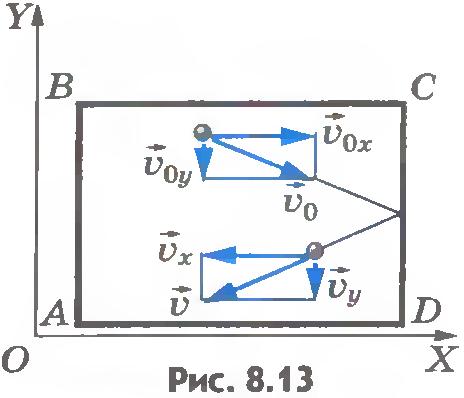
Вывод основного уравнения. Вычислим давление газа на стенкуCD сосуда ABCD площадью S, перпендикулярную координатной оси OX (рис.8.13).
При ударе молекулы о стенку ее импульс изменяется: 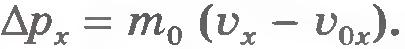 . Так как модуль скорости молекул при ударе не меняется, то . Так как модуль скорости молекул при ударе не меняется, то  . Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен . Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен 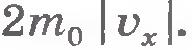 . .
Молекул много, и каждая из них передает стенке при столкновении такой же импульс. За секунду они передадут стенке импульс 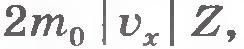 , где Z - число столкновений всех молекул со стенкой за это время. Число очевидно, прямо пропорционально концентрации молекул, т. е. числу молекул в единице объема. Кроме того, число Z пропорционально скорости молекул , где Z - число столкновений всех молекул со стенкой за это время. Число очевидно, прямо пропорционально концентрации молекул, т. е. числу молекул в единице объема. Кроме того, число Z пропорционально скорости молекул 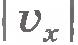 . Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой. Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки S: . Чем больше эта скорость, тем больше молекул за секунду успеет столкнуться со стенкой. Если бы молекулы «стояли на месте», то столкновений их со стенкой не было бы совсем. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки S:  . Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с . Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Значит, число ударов молекул о стенку за время 1 с 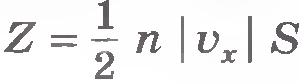 и полный импульс, переданный стенке за 1 с, равен: и полный импульс, переданный стенке за 1 с, равен:
Согласно второму закону Ньютона изменение импульса любого тела за единицу времени равно действующей на него силе: 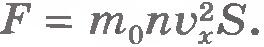 . .
Учтем, что не все молекулы имеют одно и то же значение квадрата скорости 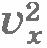 . В действительности средняя за секунду сила, действующая на стенку, пропорциональна не . В действительности средняя за секунду сила, действующая на стенку, пропорциональна не 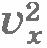 , а среднему квадрату скорости , а среднему квадрату скорости 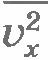 : : 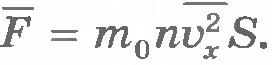 . Так как согласно формуле (8.13) . Так как согласно формуле (8.13) 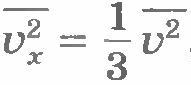 , то , то 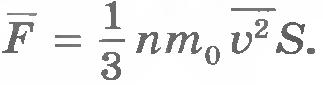 . Таким образом, давление газа на стенку сосуда равно: . Таким образом, давление газа на стенку сосуда равно:
Это и есть основное уравнение молекулярно-кинетической теории газов.
Формула (8.14) связывает макроскопическую величину - давление, которое может быть измерено манометром, - с микроскопическими величинами, характеризующими молекулы: их массой, скоростью хаотичного движения.
Связь давления со средней кинетической энергией молекул. Если через 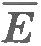 обозначить среднюю кинетическую энергию поступательного движения молекулы обозначить среднюю кинетическую энергию поступательного движения молекулы 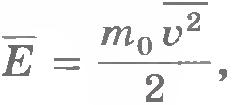 то уравнение (8.14) можно записать в виде то уравнение (8.14) можно записать в виде
Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.
В главе 9 докажем, что средняя кинетическая энергия молекул связана также и с температурой газа.
Нам удалось вычислить давление идеального газа на стенки сосуда.
Оно зависит от концентрации молекул. Кроме того, и это главное, давление газа пропорционально средней кинетической энергии молекул.
???
1. Почему молекула при соударении со стенкой действует на нее с силой, пропорциональной скорости, а давление пропорционально квадрату скорости молекулы?
2. Почему и как в основном уравнении молекулярно-кинетической теории появляется множитель 1/3?
3. Как средняя кинетическая энергия молекул зависит от концентрации газа и его давления на стенки сосуда?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|