|
|
|
| (2 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 10 класс|Физика 10 класс]]>>Физика: Статистическое истолкование необратимости процессов в природе ''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 10 класс|Физика 10 класс]]>>Физика: Статистическое истолкование необратимости процессов в природе ''' |
| | | | |
| | + | <br> |
| | | | |
| | + | <metakeywords>Физика, 10 класс, Статистическое истолкование, необратимости процессов, в природе</metakeywords> |
| | | | |
| - | <metakeywords>Физика, 10 класс, Статистическое истолкование, необратимости процессов, в природе</metakeywords>
| + | Второй закон термодинамики констатирует факт необратимости процессов в природе, но не дает ему никакого объяснения. Это объяснение может быть получено на основе молекулярно-кинетической теории.<br> '''Противоречие между обратимостью микропроцессов и необратимостью макропроцессов.'''[[Необратимость_процессов_в_природе|Необратимость]] макропроцессов выглядит парадоксально, потому что все микропроцессы обратимы во времени. Уравнения движения отдельных микрочастиц, как классические, так и квантовые, обратимы во времени, ибо никаких сил трения, зависящих от скорости, не содержат. Сила трения - это макроскопический эффект от взаимодействия большого тела с огромным количеством молекул окружающей среды, и появление этой силы само нуждается в объяснении. Силы, посредством которых взаимодействуют микрочастицы (в первую очередь это электромагнитные силы), во времени обратимы. Уравнения Максвелла, описывающие электромагнитные взаимодействия, не меняются при замене времени ''t'' на ''-t''.<br> Если взять простейшую модель газа - совокупность упругих шариков, то газ в целом будет обнаруживать определенную направленность поведения. Например, будучи сжат в половине сосуда, он начнет расширяться и займет весь сосуд. Снова он не сожмется. Уравнения же движения каждой молекулы-шарика обратимы во времени, так как содержат только силы, зависящие от расстояний и проявляющиеся при столкновении молекул.<br> Таким образом, задача состоит не только в объяснении происхождения необратимости, но и в согласовании факта обратимости микропроцессов с фактом необратимости макропроцессов.<br> Заслуга в нахождении принципиально правильного подхода к решению этой проблемы принадлежит Больцману. Правда, некоторые аспекты проблемы необратимости до сих пор не получили исчерпывающего решения.<br> '''Житейский пример необратимости.''' Приведем простой житейский пример, имеющий прямое отношение к решению проблемы необратимости Больцманом.<br> Допустим, с понедельника вы решили начать новую жизнь. Непременным условием этого обычно является идеальный или близкий к идеальному порядок на письменном столе. Вы расставляете все предметы и книги на строго определенные места, и у вас на столе царит состояние, которое с полным правом можно назвать состоянием «порядок».<br> Что произойдет с течением времени, хорошо известно. Вы забываете ставить предметы и книги на строго определенные места, и на столе воцаряется состояние хаоса. Нетрудно понять, с чем это связано. Состоянию «порядок» отвечает только одно определенное расположение предметов, а состоянию «хаос» - несравнимо большее число. И как только предметы начинают занимать произвольные положения, не контролируемые вашей волей, на столе само собой возникает более вероятное состояние хаоса, реализуемое гораздо большим числом вариантов распределения предметов на столе.<br> В принципе именно такие соображения были высказаны Больцманом для объяснения необратимости макропроцессов.<br> '''Микроскопическое и макроскопическое состояния.''' Прежде всего нужно различать макроскопическое и микроскопическое состояния системы.<br> ''Макроскопическое'' состояние характеризуется немногим числом термодинамических параметров (давлением, объемом, температурой и др.). Именно макроскопические величины, характеризующие состояние системы в целом, имеют практическое значение.<br> ''Микроскопическое'' состояние характеризуется в общем случае заданием координат и скоростей (или импульсов) всех частиц, составляющих систему (макроскопическое тело). Это несравненно более детальная характеристика системы, знание которой совсем не требуется для описания процессов с макроскопическими телами. Более того, знание микросостояния системы фактически недостижимо из-за огромного числа частиц, слагающих ее.<br> В приведенном выше житейском примере с предметами на столе можно ввести понятие микро- и макросостояний. ''Микросостоянию'' отвечает какое-то одно определенное расположение предметов, а ''макросостоянию'' - оценка ситуации в целом: либо «порядок», либо «хаос». Вполне очевидно, что ''определенное макросостояние может быть реализовано огромным числом различных микросостоянии''. Так, переход одной молекулы из данной точки пространства в другую точку или изменение ее скорости в результате столкновения изменяет микросостояние системы, но, конечно, не меняет [[Термодинамические_подходы_к_сущности_жизни|термодинамических]] параметров и, следовательно, макросостояния системы.<br> Теперь введем гипотезу, не столь очевидную, как предшествующие утверждения: ''все микроскопические состояния изолированной системы равновероятны; ни одно из них не выделено, не занимает преимущественного положения.'' Это предположение фактически эквивалентно гипотезе о хаотичном характере теплового движения молекул.<br> '''Вероятность состояния.''' С течением времени микросостояния непрерывно сменяют друг друга. Время пребывания системы в определенном макроскопическом состоянии пропорционально, очевидно, числу микросостояний ''Z<sub>1</sub>'', которые реализуют данное состояние. Если через ''Z'' обозначить полное число микросостояний системы, то вероятность состояния ''W'' можно определить так:<br>[[Image:A81-1.jpg|center|67x34px|A81-1.jpg]] ''' Вероятность макроскопического состояния равна отношению числа микросостояний, реализующих макросостояние, к полному числу возможных микросостояний.'''<br> '''Переход системы к наиболее вероятному состоянию.''' Чем больше ''Z<sub>1</sub>'', тем больше вероятность данного макросостояния и тем большее время система будет находиться в этом состоянии. Таким образом, ''эволюция системы про исходит в направлении перехода от маловероятных со стояний к состояниям более вероятным''. Именно с этим связана необратимость течения макроскопических процессов, несмотря на обратимость законов, управляющих движением отдельных частиц. Обратный процесс не является невозможным, он просто маловероятен. Так как все микросостояния равновероятны, то в принципе может возникнуть макросостояние, реализуемое малым числом микросостояний, но это чрезвычайно редкое событие. Мы не должны удивляться, если никогда не увидим их. Наиболее вероятно состояние теплового равновесия. Ему отвечает наибольшее число микросостояний.<br> Легко понять, почему механическая энергия самопроизвольно переходит во внутреннюю. Механическое движение системы (или тела) - это упорядоченное движение, когда все части системы перемещаются определенным образом. Упорядоченному движению отвечает небольшое число микросостояний по сравнению с беспорядочным тепловым движением. Поэтому маловероятное состояние упорядоченного механического движения само собой превращается в беспорядочное тепловое движение, реализуемое гораздо большим числом микросостояний.<br> Менее нагляден процесс перехода теплоты от горячего тела к холодному. Но и здесь сущность необратимости та же. В начале теплообмена есть две группы молекул: молекулы с более высокой средней кинетической энергией у горячего тела и молекулы с низкой средней кинетической энергией у холодного. При установлении теплового равновесия в конце процесса все молекулы окажутся принадлежащими к одной группе молекул с одной и той же средней [[Кинетическая_энергия_и_ее_изменение|кинетической энергией]]. Более упорядоченное состояние с разделением молекул на две группы перестает существовать.<br> Итак, необратимость процессов связана с тем, что неравновесные макроскопические состояния маловероятны. Эти состояния либо возникают естественным путем в результате эволюции Вселенной, либо создаются искусственно человеком. Например, мы получаем сильно неравновесные состояния, нагревая рабочее тело теплового двигателя до температур, на сотни градусов превышающих температуру окружающей среды.<br> '''Расширение газа из четырех молекул.''' Рассмотрим простой пример, позволяющий вычислить вероятности различных состояний и наглядно показывающий, как увеличение числа частиц в системе приводит к тому, что процессы становятся необратимыми, несмотря на обратимость уравнений движения микрочастиц.<br> Пусть в сосуде имеется газ, состоящий всего лишь из четырех молекул. Вначале все молекулы находятся в левой половине сосуда, отделенной перегородкой от правой половины (''рис.13.10, а''). Уберем перегородку, и газ начнет расширяться, занимая весь сосуд. Посмотрим, какова вероятность того, что газ опять сожмется, т. е. молекулы снова соберутся в одной половине сосуда.<br>[[Image:A13.10.jpg|center|535x292px|физика]] В нашем примере макросостояние будет характеризоваться указанием числа молекул в одной половине сосуда безотносительно к тому, какие именно молекулы здесь находятся. Микросостояния задаются распределением молекул по половинам сосуда с указанием того, какие именно молекулы занимают данную половину сосуда. Пронумеруем [[Молекулы_и_атомы|молекулы]] цифрами 1, 2, 3, 4. Возможны 16 различных микросостояний, все они изображены на рисунке 13.10, а-д.<br> Вероятность того, что все молекулы соберутся в левой половине сосуда, равна:<br>[[Image:A81-2.jpg|center|110x34px|A81-2.jpg]] так как данному макросостоянию соответствует одно микросостояние из полного их числа 16 (см. ''рис.13.10, а, б'').<br> Вероятность же того, что молекулы распределятся поровну, будет в 6 раз больше:<br>[[Image:A81-3.jpg|center|101x31px|A81-3.jpg]]так как данному макросостоянию соответствует 6 микросостояний из полного их числа 16 (см. ''рис.13.10, д'').<br> Вероятность того, что в одной половине сосуда, например левой, будет три молекулы, а в другой соответственно одна молекула, равна (см.''рис.13.10, в, г''):<br>[[Image:A81-4.jpg|center|108x34px|A81-4.jpg]] Большую часть времени молекулы будут распределены в половинках сосуда поровну: это наиболее вероятное состояние. Но примерно 2/16 интервала времени наблюдения молекулы будут занимать одну из половинок сосуда. Таким образом, процесс расширения газа в данном примере обратим и газ снова сжимается через сравнительно небольшой промежуток времени.<br> '''Необратимость расширения газа с большим числом молекул. '''Описанная выше обратимость возможна лишь при небольшом числе молекул. Если же число молекул становится огромным, то результат существенно иной.<br> Подсчитаем вероятность того, что молекулы вновь соберутся в одной половинке сосуда после расширения, если число молекул произвольно велико.<br> Молекулы идеального газа движутся практически независимо друг от друга. Для одной молекулы вероятность того, что она окажется в левой половине сосуда, равна, очевидно, 1/2. Такова же вероятность и для другой молекулы. Эти события независимы, и вероятность того, что первая и вторая молекулы окажутся в левой половине сосуда, равна произведению вероятностей событии:1/2•1/2=1/4=1/2<sup>2</sup>. Для трех молекул вероятность их нахождения в левой половине сосуда равна 1/2<sup>3</sup>, а для четырех - 1/2<sup>4</sup>. Именно такое значение вероятности мы и получили при детальном рассмотрении распределения молекул по сосуду.<br> Но если взять реальное число молекул газа в 1 см<sup>3</sup> при нормальных условиях (''n''=3•10<sup>19</sup>), то вероятность того, что молекулы соберутся в одной половине сосуда объемом 1 см<sup>3</sup>, будет совершенно ничтожна:<br>[[Image:A81-5.jpg|center|78x37px|A81-5.jpg]] Таким образом, только из-за большого числа молекул в макросистемах процессы в природе оказываются практически необратимыми. В принципе обратные процессы возможны, но вероятность их близка к нулю. Не противоречит, строго говоря, законам природы процесс, в результате которого при случайном движении молекул все они соберутся в одной половине класса, а учащиеся в другой половине класса задохнутся. Но реально это событие никогда не происходило в прошлом и не произойдет в будущем. Слишком мала вероятность подобного события, чтобы оно когда-либо случилось за все время существования Вселенной в современном ее состоянии - около нескольких миллиардов лет.<br> По приблизительным оценкам, эта вероятность примерно такого же порядка, как и вероятность того, что 20 000 обезьян, хаотично ударяя по клавишам пишущих машинок, напечатают без единой ошибки «Войну и мир» Л. Н. [[Лев_ТОЛСТÓЙ_(1828–1910)._Життєвий_і_творчий_шлях_письменника._Творчість_Льва_Толстого_як_найповніший_вияв_можливостей_реалістичної_літератури|Толстого]]. В принципе это возможно, но реально никогда не произойдет.<br> '''Стрела времени.''' Во всех процессах существует выделенное направление, в котором процессы идут сами собой от более упорядоченного состояния к менее упорядоченному. Чем больше порядок в системе, тем сложнее восстановить его из беспорядка. Несравненно проще разбить стекло, чем изготовить новое и вставить его в раму. Гораздо проще убить живое существо, чем возвратить его к жизни, если это вообще возможно. «Бог сотворил маленькую букашку. Если ты ее раздавишь, она умрет» - такой эпиграф поставил американский биохимик Сент Дьерди к своей книге «[[Электроэнергетика| Биоэнергетика]] ».<br> Выделенное направление времени - ''стрела времени'', - воспринимаемое нами, очевидно, связано с направленностью процессов в мире.<br> '''Границы применимости второго закона [[Первый_закон_термодинамики|термодинамики]].''' Вероятность обратных процессов перехода от равновесных состояний к неравновесным для макроскопических систем в целом очень мала. Но для малых объемов, содержащих небольшое число молекул, вероятность отклонения от равновесия становится заметной. Такие случайные отклонения системы от равновесия называются ''флуктуациями''. Именно флуктуациями плотности газа в областях порядка длины световой волны объясняются рассеяние света в атмосфере Земли и голубой цвет неба. Флуктуации давления в малых объемах объясняют броуновское движение.<br> Наблюдение флуктуации служит важнейшим доказательством правильности созданной Больцманом статистической теории необратимости макропроцессов. ''Второй закон термодинамики выполняется только для систем с огромным числом частиц.'' В малых объемах становятся существенными отклонения от этого закона.<br> Необратимость процессов в природе связана со стремлением систем к переходу в наиболее вероятное состояние, которому отвечает максимальный беспорядок.<br> |
| | | | |
| | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| | | | |
| - | | + | <br> <sub>Планирования [[Физика и астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика 10 класс|по физике для 10 класса]]</sub> |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс''
| + | |
| - | | + | |
| - | <br> <sub>Планирования [[Физика_и_астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика_10_класс|по физике для 10 класса]]</sub> | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 12:06, 5 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Статистическое истолкование необратимости процессов в природе
Второй закон термодинамики констатирует факт необратимости процессов в природе, но не дает ему никакого объяснения. Это объяснение может быть получено на основе молекулярно-кинетической теории.
Противоречие между обратимостью микропроцессов и необратимостью макропроцессов.Необратимость макропроцессов выглядит парадоксально, потому что все микропроцессы обратимы во времени. Уравнения движения отдельных микрочастиц, как классические, так и квантовые, обратимы во времени, ибо никаких сил трения, зависящих от скорости, не содержат. Сила трения - это макроскопический эффект от взаимодействия большого тела с огромным количеством молекул окружающей среды, и появление этой силы само нуждается в объяснении. Силы, посредством которых взаимодействуют микрочастицы (в первую очередь это электромагнитные силы), во времени обратимы. Уравнения Максвелла, описывающие электромагнитные взаимодействия, не меняются при замене времени t на -t.
Если взять простейшую модель газа - совокупность упругих шариков, то газ в целом будет обнаруживать определенную направленность поведения. Например, будучи сжат в половине сосуда, он начнет расширяться и займет весь сосуд. Снова он не сожмется. Уравнения же движения каждой молекулы-шарика обратимы во времени, так как содержат только силы, зависящие от расстояний и проявляющиеся при столкновении молекул.
Таким образом, задача состоит не только в объяснении происхождения необратимости, но и в согласовании факта обратимости микропроцессов с фактом необратимости макропроцессов.
Заслуга в нахождении принципиально правильного подхода к решению этой проблемы принадлежит Больцману. Правда, некоторые аспекты проблемы необратимости до сих пор не получили исчерпывающего решения.
Житейский пример необратимости. Приведем простой житейский пример, имеющий прямое отношение к решению проблемы необратимости Больцманом.
Допустим, с понедельника вы решили начать новую жизнь. Непременным условием этого обычно является идеальный или близкий к идеальному порядок на письменном столе. Вы расставляете все предметы и книги на строго определенные места, и у вас на столе царит состояние, которое с полным правом можно назвать состоянием «порядок».
Что произойдет с течением времени, хорошо известно. Вы забываете ставить предметы и книги на строго определенные места, и на столе воцаряется состояние хаоса. Нетрудно понять, с чем это связано. Состоянию «порядок» отвечает только одно определенное расположение предметов, а состоянию «хаос» - несравнимо большее число. И как только предметы начинают занимать произвольные положения, не контролируемые вашей волей, на столе само собой возникает более вероятное состояние хаоса, реализуемое гораздо большим числом вариантов распределения предметов на столе.
В принципе именно такие соображения были высказаны Больцманом для объяснения необратимости макропроцессов.
Микроскопическое и макроскопическое состояния. Прежде всего нужно различать макроскопическое и микроскопическое состояния системы.
Макроскопическое состояние характеризуется немногим числом термодинамических параметров (давлением, объемом, температурой и др.). Именно макроскопические величины, характеризующие состояние системы в целом, имеют практическое значение.
Микроскопическое состояние характеризуется в общем случае заданием координат и скоростей (или импульсов) всех частиц, составляющих систему (макроскопическое тело). Это несравненно более детальная характеристика системы, знание которой совсем не требуется для описания процессов с макроскопическими телами. Более того, знание микросостояния системы фактически недостижимо из-за огромного числа частиц, слагающих ее.
В приведенном выше житейском примере с предметами на столе можно ввести понятие микро- и макросостояний. Микросостоянию отвечает какое-то одно определенное расположение предметов, а макросостоянию - оценка ситуации в целом: либо «порядок», либо «хаос». Вполне очевидно, что определенное макросостояние может быть реализовано огромным числом различных микросостоянии. Так, переход одной молекулы из данной точки пространства в другую точку или изменение ее скорости в результате столкновения изменяет микросостояние системы, но, конечно, не меняет термодинамических параметров и, следовательно, макросостояния системы.
Теперь введем гипотезу, не столь очевидную, как предшествующие утверждения: все микроскопические состояния изолированной системы равновероятны; ни одно из них не выделено, не занимает преимущественного положения. Это предположение фактически эквивалентно гипотезе о хаотичном характере теплового движения молекул.
Вероятность состояния. С течением времени микросостояния непрерывно сменяют друг друга. Время пребывания системы в определенном макроскопическом состоянии пропорционально, очевидно, числу микросостояний Z1, которые реализуют данное состояние. Если через Z обозначить полное число микросостояний системы, то вероятность состояния W можно определить так:
Вероятность макроскопического состояния равна отношению числа микросостояний, реализующих макросостояние, к полному числу возможных микросостояний.
Переход системы к наиболее вероятному состоянию. Чем больше Z1, тем больше вероятность данного макросостояния и тем большее время система будет находиться в этом состоянии. Таким образом, эволюция системы про исходит в направлении перехода от маловероятных со стояний к состояниям более вероятным. Именно с этим связана необратимость течения макроскопических процессов, несмотря на обратимость законов, управляющих движением отдельных частиц. Обратный процесс не является невозможным, он просто маловероятен. Так как все микросостояния равновероятны, то в принципе может возникнуть макросостояние, реализуемое малым числом микросостояний, но это чрезвычайно редкое событие. Мы не должны удивляться, если никогда не увидим их. Наиболее вероятно состояние теплового равновесия. Ему отвечает наибольшее число микросостояний.
Легко понять, почему механическая энергия самопроизвольно переходит во внутреннюю. Механическое движение системы (или тела) - это упорядоченное движение, когда все части системы перемещаются определенным образом. Упорядоченному движению отвечает небольшое число микросостояний по сравнению с беспорядочным тепловым движением. Поэтому маловероятное состояние упорядоченного механического движения само собой превращается в беспорядочное тепловое движение, реализуемое гораздо большим числом микросостояний.
Менее нагляден процесс перехода теплоты от горячего тела к холодному. Но и здесь сущность необратимости та же. В начале теплообмена есть две группы молекул: молекулы с более высокой средней кинетической энергией у горячего тела и молекулы с низкой средней кинетической энергией у холодного. При установлении теплового равновесия в конце процесса все молекулы окажутся принадлежащими к одной группе молекул с одной и той же средней кинетической энергией. Более упорядоченное состояние с разделением молекул на две группы перестает существовать.
Итак, необратимость процессов связана с тем, что неравновесные макроскопические состояния маловероятны. Эти состояния либо возникают естественным путем в результате эволюции Вселенной, либо создаются искусственно человеком. Например, мы получаем сильно неравновесные состояния, нагревая рабочее тело теплового двигателя до температур, на сотни градусов превышающих температуру окружающей среды.
Расширение газа из четырех молекул. Рассмотрим простой пример, позволяющий вычислить вероятности различных состояний и наглядно показывающий, как увеличение числа частиц в системе приводит к тому, что процессы становятся необратимыми, несмотря на обратимость уравнений движения микрочастиц.
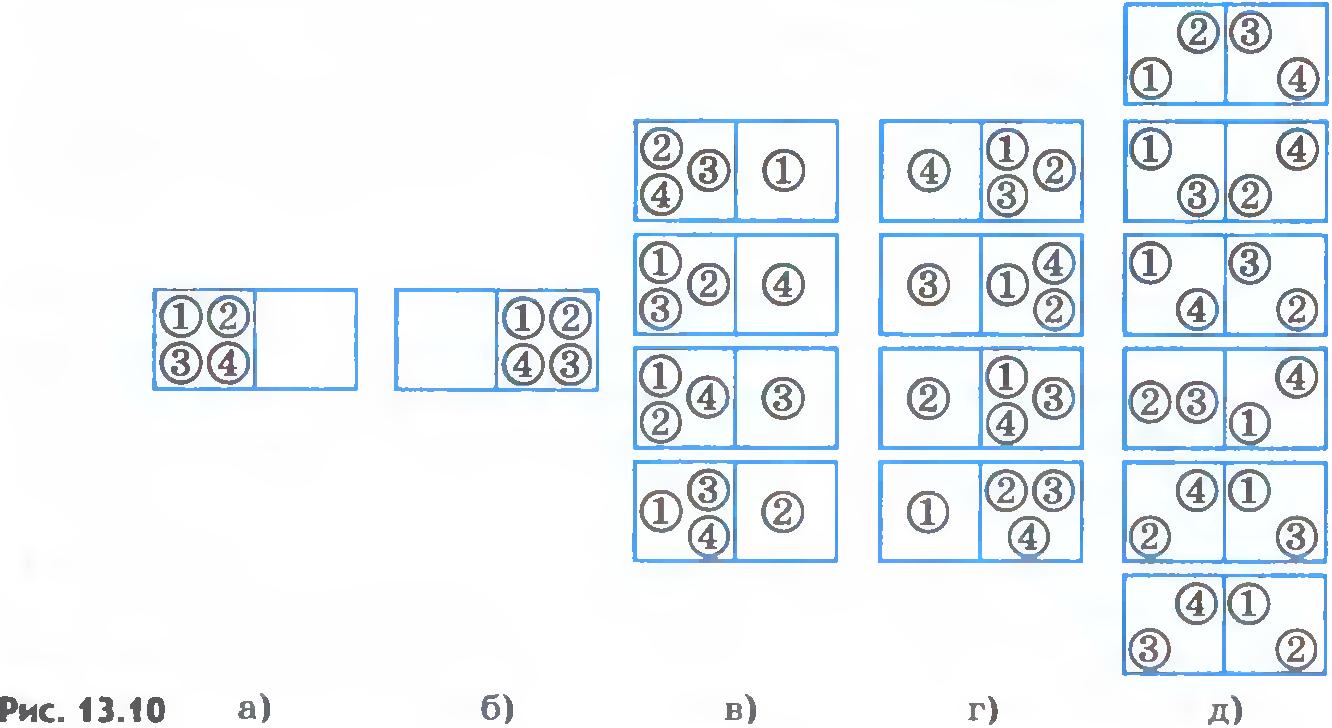
Пусть в сосуде имеется газ, состоящий всего лишь из четырех молекул. Вначале все молекулы находятся в левой половине сосуда, отделенной перегородкой от правой половины (рис.13.10, а). Уберем перегородку, и газ начнет расширяться, занимая весь сосуд. Посмотрим, какова вероятность того, что газ опять сожмется, т. е. молекулы снова соберутся в одной половине сосуда.
В нашем примере макросостояние будет характеризоваться указанием числа молекул в одной половине сосуда безотносительно к тому, какие именно молекулы здесь находятся. Микросостояния задаются распределением молекул по половинам сосуда с указанием того, какие именно молекулы занимают данную половину сосуда. Пронумеруем молекулы цифрами 1, 2, 3, 4. Возможны 16 различных микросостояний, все они изображены на рисунке 13.10, а-д.
Вероятность того, что все молекулы соберутся в левой половине сосуда, равна:
так как данному макросостоянию соответствует одно микросостояние из полного их числа 16 (см. рис.13.10, а, б).
Вероятность же того, что молекулы распределятся поровну, будет в 6 раз больше:
так как данному макросостоянию соответствует 6 микросостояний из полного их числа 16 (см. рис.13.10, д).
Вероятность того, что в одной половине сосуда, например левой, будет три молекулы, а в другой соответственно одна молекула, равна (см.рис.13.10, в, г):
Большую часть времени молекулы будут распределены в половинках сосуда поровну: это наиболее вероятное состояние. Но примерно 2/16 интервала времени наблюдения молекулы будут занимать одну из половинок сосуда. Таким образом, процесс расширения газа в данном примере обратим и газ снова сжимается через сравнительно небольшой промежуток времени.
Необратимость расширения газа с большим числом молекул. Описанная выше обратимость возможна лишь при небольшом числе молекул. Если же число молекул становится огромным, то результат существенно иной.
Подсчитаем вероятность того, что молекулы вновь соберутся в одной половинке сосуда после расширения, если число молекул произвольно велико.
Молекулы идеального газа движутся практически независимо друг от друга. Для одной молекулы вероятность того, что она окажется в левой половине сосуда, равна, очевидно, 1/2. Такова же вероятность и для другой молекулы. Эти события независимы, и вероятность того, что первая и вторая молекулы окажутся в левой половине сосуда, равна произведению вероятностей событии:1/2•1/2=1/4=1/22. Для трех молекул вероятность их нахождения в левой половине сосуда равна 1/23, а для четырех - 1/24. Именно такое значение вероятности мы и получили при детальном рассмотрении распределения молекул по сосуду.
Но если взять реальное число молекул газа в 1 см3 при нормальных условиях (n=3•1019), то вероятность того, что молекулы соберутся в одной половине сосуда объемом 1 см3, будет совершенно ничтожна:
Таким образом, только из-за большого числа молекул в макросистемах процессы в природе оказываются практически необратимыми. В принципе обратные процессы возможны, но вероятность их близка к нулю. Не противоречит, строго говоря, законам природы процесс, в результате которого при случайном движении молекул все они соберутся в одной половине класса, а учащиеся в другой половине класса задохнутся. Но реально это событие никогда не происходило в прошлом и не произойдет в будущем. Слишком мала вероятность подобного события, чтобы оно когда-либо случилось за все время существования Вселенной в современном ее состоянии - около нескольких миллиардов лет.
По приблизительным оценкам, эта вероятность примерно такого же порядка, как и вероятность того, что 20 000 обезьян, хаотично ударяя по клавишам пишущих машинок, напечатают без единой ошибки «Войну и мир» Л. Н. Толстого. В принципе это возможно, но реально никогда не произойдет.
Стрела времени. Во всех процессах существует выделенное направление, в котором процессы идут сами собой от более упорядоченного состояния к менее упорядоченному. Чем больше порядок в системе, тем сложнее восстановить его из беспорядка. Несравненно проще разбить стекло, чем изготовить новое и вставить его в раму. Гораздо проще убить живое существо, чем возвратить его к жизни, если это вообще возможно. «Бог сотворил маленькую букашку. Если ты ее раздавишь, она умрет» - такой эпиграф поставил американский биохимик Сент Дьерди к своей книге « Биоэнергетика ».
Выделенное направление времени - стрела времени, - воспринимаемое нами, очевидно, связано с направленностью процессов в мире.
Границы применимости второго закона термодинамики. Вероятность обратных процессов перехода от равновесных состояний к неравновесным для макроскопических систем в целом очень мала. Но для малых объемов, содержащих небольшое число молекул, вероятность отклонения от равновесия становится заметной. Такие случайные отклонения системы от равновесия называются флуктуациями. Именно флуктуациями плотности газа в областях порядка длины световой волны объясняются рассеяние света в атмосфере Земли и голубой цвет неба. Флуктуации давления в малых объемах объясняют броуновское движение.
Наблюдение флуктуации служит важнейшим доказательством правильности созданной Больцманом статистической теории необратимости макропроцессов. Второй закон термодинамики выполняется только для систем с огромным числом частиц. В малых объемах становятся существенными отклонения от этого закона.
Необратимость процессов в природе связана со стремлением систем к переходу в наиболее вероятное состояние, которому отвечает максимальный беспорядок.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
