|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| | + | <metakeywords>Информатика, класc, урок, на тему, 11 класc, Представление зависимостей между величинами, информатика, базы данных, модель, диаграмма</metakeywords> |
| | + | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: Представление зависимостей между величинами '''<br> | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: Представление зависимостей между величинами '''<br> |
| | | | |
| - | ''<br>''<metakeywords>Представление зависимостей между величинами</metakeywords><br>
| + | <br> <br>'''Представление зависимостей между величинами ''' ''<br> ''<br> |
| | | | |
| - | <br>''' Представление зависимостей между величинами ''' ''<br> ''<br>
| + | Решение задач планирования и управления постоянно требует учета зависимостей одних факторов от других. |
| | | | |
| - | '' Решение задач планирования и управления постоянно требует учета зависимостей одних факторов от других. Примеры зависимостей:''<br> | + | '''Примеры зависимостей''':<br> |
| | | | |
| - | '' 1) время падения тела на землю зависит от первоначальной высоты;''<br>
| + | 1) время падения тела на землю зависит от первоначальной высоты;<br> |
| | | | |
| - | '' 2) давление зависит от температуры газа в баллоне;''<br>
| + | 2) давление зависит от температуры газа в баллоне;<br> |
| | | | |
| - | '' 3) частота заболевания жителей бронхиальной астмой зависит от качества городского воздуха.''<br>
| + | 3) частота [http://xvatit.com/sneeze/ '''заболевания'''] жителей бронхиальной астмой зависит от качества городского воздуха.<br> |
| | | | |
| - | '' Рассмотрим различные методы представления зависимостей.''<br>
| + | <br> |
| | | | |
| - | '' Всякое исследование нужно начинать с выделения количественных характеристик исследуемого объекта (процесса,<br>явления). Такие характеристики называются ''величинами'''''.'''''
| + | '''Рассмотрим различные методы представления зависимостей.'''<br> |
| | | | |
| - | '' С понятием величины вы уже встречались в базовом курсе информатики. Напомним, что со всякой величиной связны три основные свойства: имя, значение, тип.''<br>
| + | Всякое исследование нужно начинать с выделения количественных характеристик исследуемого объекта (процесса, явления). Такие характеристики называются величинами'''.''' |
| | | | |
| - | '' Имя величины может быть полным (подчеркивающим ее смысл,а может быть символическим.Примером имени является «Давление газа»; а символическое имя для этой же величины — Р. В базах данных величинами являются поля записей. Для них, как правило, используются полные имена, например: «Фамилия», «Вес»» «Оценка» и т. п. В физике и других науках, использующих математический аппарат, применяются символические имена для обозначения величин. Чтобы не терялся смысл, для определенных величин используются стандартные имена. Например, время обозначают буквой t скорость — V, силу — F и так далее. '''''<br>''' | + | С понятием величины вы уже встречались в базовом курсе '''[[Предыстория информатики|информатики]]'''. Напомним, что со всякой величиной связны три основные свойства: имя, значение, тип.<br> |
| | | | |
| - | '' Если значение величины не изменяется, то она называется постоянной величиной или константой. Пример константы — число Пифагора п =З,14159... Величина, меняющая свое значение, называется '''переменной'''.''<br>
| + | Имя величины может быть полным (подчеркивающим ее смысл,а может быть символическим. Примером имени является «Давление газа»; а символическое имя для этой же величины — Р. В '''[[Системи управління базами даних. Повні уроки|базах данных]]''' величинами являются поля записей. Для них, как правило, используются полные имена, например: «Фамилия», «Вес»» «Оценка» и т. п. В физике и других науках, использующих математический аппарат, применяются символические имена для обозначения величин. Чтобы не терялся смысл, для определенных величин используются стандартные имена. Например, время обозначают буквой t скорость — V, силу — F и так далее. '''<br>''' |
| | | | |
| - | ''Например, в описании процесса падения тела переменными величинами являются высота (Н) и время падения (t).<br> <br> Третьим свойством величины является ее тип. С понятием типа величине вы также встречались в базах данных. Тип определяет мужество значений, которые может принимать величина. Основные етипы величин: числовой, символьный, логический. Поскольку в данном разделе мы будем говорить лишь о количественных характеристиках, то и рассматриваться будут только величины числового типа.<br> А теперь вернемся к приведенным в начале параграфа примерам 1-3 и обозначим (поименуем) все переменные величины, зависимости между которыми нас будут интересовать. Кроме имен укажем размерности величин. Размерности определяют единицы, в которых представляются значения величин:''<br>
| + | Если значение величины не изменяется, то она называется постоянной величиной или константой. Пример константы — число Пифагора n =З,14159... Величина, меняющая свое значение, называется '''переменной'''.<br> |
| | | | |
| - | '' 1) t (сек) — время падения; Н (ж) — высота падения. Зависимость будем представлять, пренебрегая учетом сопротивления воздуха. Ускорение свободного падения g (м/сек<sup>2</sup>) — константа.''
| + | Например, в описании процесса падения тела переменными величинами являются высота (Н) и время падения (t).<br> |
| | | | |
| - | '' 2) Р (кг/м<sup>2</sup>) — давление газа; t°С — температура газа. Давление при нуле градусов Р0 считается константой для данного газа.''
| + | Третьим свойством величины является ее тип. С понятием типа величине вы также встречались в базах данных. Тип определяет мужество значений, которые может принимать величина. Основные типы величин: числовой, символьный, логический. Поскольку в данном разделе мы будем говорить лишь о количественных характеристиках, то и рассматриваться будут только величины числового типа.<br> |
| | | | |
| - | '' 3) Загрязненность воздуха будем характеризовать концентрацией примесей (каких именно, будет сказано позже) — С(мг/куб. м).''
| + | А теперь вернемся к приведенным в начале параграфа примерам 1-3 и обозначим (поименуем) все переменные величины, зависимости между которыми нас будут интересовать. Кроме имен укажем размерности величин. |
| | | | |
| - | '' Единица измерения — масса примесей, содержащихся в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости будем характеризовать числом хронических больных астмой, приходящимся на 1000 жителей данного города — Р (бол./тыс).'' | + | '''Размерности определяют единицы, в которых представляются значения величин:'''<br> |
| | | | |
| - | '' Если зависимое между величинами удается представить в математической форме, то мы имеем математическую модель.''
| + | 1) t (сек) — время падения; Н (ж) — высота падения. Зависимость будем представлять, пренебрегая учетом сопротивления воздуха. Ускорение свободного падения g (м/сек<sup>2</sup>) — константа. |
| | | | |
| - | '' '''Математическая модель''' - это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики.''
| + | 2) Р (кг/м<sup>2</sup>) — давление газа; t°С — температура газа. Давление при нуле градусов Р0 считается константой для данного газа. |
| | | | |
| - | '' Хорошо известны математические модели для первых двух примеров из перечисленных выше. Они отражают физические законы и представляются в виде формул:<br><br>[[Image:Инф92.jpg]]''
| + | 3) Загрязненность воздуха будем характеризовать концентрацией примесей (каких именно, будет сказано позже) — С(мг/куб. м). |
| | | | |
| - | ''<br> Это примеры зависимостей, представленных в функции пильной форме. Первую зависимость называют корневой (время пропорционально квадратному корню от высоты), вторую — линейной (давление прямо пропорционально температуре).<br>В более сложных задачах математические модели представляются в виде уравнений или систем уравнений. В этом случае для извлечения функциональной зависимости величин нужно уметь решать эти уравнения. В конце данной главы будет рассмотрен пример математической модели, которая выражается системой неравенств.''
| + | Единица измерения — масса примесей, содержащихся в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости будем характеризовать числом хронических больных астмой, приходящимся на 1000 жителей данного города — Р (бол./тыс). |
| | | | |
| - | '' Рассмотрим примеры двух других способов представления зависимостей между величинами: табличного и графического. ''
| + | Если зависимое между величинами удается представить в математической форме, то мы имеем математическую '''[[Информационные модели|модель]]'''. |
| | | | |
| - | '' Представьте себе, что мы решили проверить закон свободного падения тела экспериментальным путем. Эксперимент организовали следующим образом; бросаем стальной шарик с балкона 2-го этажа, 3-го этажа (и так далее) десятиэтажного дома, замеряя высоту начального положения шарика и время падения. По результатам эксперимента мы составили таблицу и нарисовали график.<br> <br>[[Image:Инф93.jpg]]'' | + | '''Математическая модель''' - это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики. |
| | | | |
| - | ''<br>Рис. 2.11. Табличное и графическое представление зависимости времени падения тела от высоты<br><br> Если каждую пару значений Н и t из данной таблицы подставить в приведенную выше формулу зависимости высоты от времени, то она превратится в равенство (с точностью до погрешности измерений). Значит, модель работает хорошо. (Однако если сбрасывать не стальной шарик, а большой легкий мяч, то данная модель будет меньше соответствовать формуле, а если надувной шарик, то совсем не будет соответствовать — как вы думаете, почему?)'' | + | Хорошо известны математические модели для первых двух примеров из перечисленных выше. Они отражают физические законы и представляются в виде формул:''<br><br>[[Image:Инф92.jpg|240px|Формулы]]''<br>Это примеры зависимостей, представленных в функции пильной форме. Первую зависимость называют корневой (время пропорционально квадратному корню от высоты), вторую — линейной (давление прямо пропорционально температуре).<br> |
| | | | |
| - | '' В этом примере мы рассмотрели три способа отображения зависимости величин: функциональный (формула), табличный и графический. Однако математической моделью процесса падения тела на землю можно назвать только формулу. Почему? Потому что формула универсальна. Она позволяет определить время падения тела с любой высоты, а не только для того экспериментального набора значений Н, который отображен на рис. 2.11.''
| + | В более сложных задачах математические модели представляются в виде уравнений или систем уравнений. В этом случае для извлечения функциональной зависимости величин нужно уметь решать эти уравнения. В конце данной главы будет рассмотрен пример математической модели, которая выражается системой неравенств. |
| | | | |
| - | '' Кроме того, таблица и диаграмма (график) констатируют факты, а математическая модель позволяет прогнозировать, предсказывать путем расчетов .''
| + | Рассмотрим примеры двух других способов представления зависимостей между величинами: табличного и графического. |
| | | | |
| - | '' Точно так же тремя способами можно отобразить зависимость давления от температуры. Оба примера связаны с известными физическими законами — законами природы. Знания физических законов позволяют производить точные расчеты, они лежит в основе современной техники.<br><br><br> '''Коротко о главном'''<br><br><br> Величина — некоторая количественная характеристика объекта.''
| + | Представьте себе, что мы решили проверить закон свободного падения тела экспериментальным путем. Эксперимент организовали следующим образом; бросаем стальной шарик с балкона 2-го этажа, 3-го этажа (и так далее) десятиэтажного дома, замеряя высоту начального положения шарика и время падения. По результатам эксперимента мы составили таблицу и нарисовали график.''<br> <br>[[Image:Инф93.jpg|550px|Табличное и графическое представление зависимости времени падения тела от высоты]]''''<br>'''Рис. 2.11. Табличное и графическое представление зависимости времени падения тела от высоты<br><br>''Если каждую пару значений Н и t из данной таблицы подставить в приведенную выше формулу зависимости высоты от времени, то она превратится в равенство (с точностью до погрешности измерений). Значит, модель работает хорошо. (Однако если сбрасывать не стальной шарик, а большой легкий мяч, то данная модель будет меньше соответствовать формуле, а если надувной шарик, то совсем не будет соответствовать — как вы думаете, почему?) |
| | | | |
| - | '' Зависимости между величинами могут быть представлены в виде математической модели, в табличной и графической формах.''
| + | В этом примере мы рассмотрели три способа отображения зависимости величин: функциональный (формула), табличный и графический. Однако математической моделью процесса падения тела на землю можно назвать только формулу. Почему? Потому что формула универсальна. Она позволяет определить время падения тела с любой высоты, а не только для того экспериментального набора значений Н, который отображен на рис. 2.11. |
| | | | |
| - | '' Зависимость, представленная в виде формулы, является математической моделью.<br><br><br> '''Вопросы и задания'''<br><br> 1. а) Какие вам известны формы представления зависимостей<br>между величинами?''
| + | Кроме того, таблица и '''[[Мастер диаграмм в табличном процессоре MS Excel|диаграмма]]''' (график) констатируют факты, а математическая модель позволяет прогнозировать, предсказывать путем расчетов . |
| | | | |
| - | '' б) Что такое математическая модель?'' | + | Точно так же тремя способами можно отобразить зависимость давления от температуры. Оба примера связаны с известными физическими законами — законами природы. Знания физических законов позволяют производить точные расчеты, они лежит в основе современной техники.''<br><br>'''''Коротко о главном'''<br><br>Величина — некоторая количественная характеристика объекта. |
| | | | |
| - | '' в) Может ли математическая модель включать в себя только константы?''
| + | Зависимости между величинами могут быть представлены в виде математической модели, в табличной и графической формах. |
| | | | |
| - | '' 2. Приведите пример известной вам функциональной зависимости (формулы) между характеристиками некоторой системы.'' | + | Зависимость, представленная в виде формулы, является математической моделью.<br><br>'''Вопросы и задания'''''<br><br>1. а) Какие вам известны формы представления зависимостей между величинами?'' |
| | | | |
| - | '' 3. Обоснуйте преимущества и недостатки каждой из трех форм представления зависимостей.<br><br>Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11'' | + | ''б) Что такое математическая модель?'' |
| | + | |
| | + | ''в) Может ли математическая модель включать в себя только константы?'' |
| | + | |
| | + | ''2. Приведите пример известной вам функциональной зависимости (формулы) между характеристиками некоторой системы.'' |
| | + | |
| | + | ''3. Обоснуйте преимущества и недостатки каждой из трех форм представления зависимостей.'' |
| | + | |
| | + | <br> ''<br><br>Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11'' |
| | | | |
| | ''Отослано читателями из интернет-сайтов''<br><br> | | ''Отослано читателями из интернет-сайтов''<br><br> |
| Строка 70: |
Строка 80: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 04:58, 7 июля 2012
Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: Представление зависимостей между величинами
Представление зависимостей между величинами
Решение задач планирования и управления постоянно требует учета зависимостей одних факторов от других.
Примеры зависимостей:
1) время падения тела на землю зависит от первоначальной высоты;
2) давление зависит от температуры газа в баллоне;
3) частота заболевания жителей бронхиальной астмой зависит от качества городского воздуха.
Рассмотрим различные методы представления зависимостей.
Всякое исследование нужно начинать с выделения количественных характеристик исследуемого объекта (процесса, явления). Такие характеристики называются величинами.
С понятием величины вы уже встречались в базовом курсе информатики. Напомним, что со всякой величиной связны три основные свойства: имя, значение, тип.
Имя величины может быть полным (подчеркивающим ее смысл,а может быть символическим. Примером имени является «Давление газа»; а символическое имя для этой же величины — Р. В базах данных величинами являются поля записей. Для них, как правило, используются полные имена, например: «Фамилия», «Вес»» «Оценка» и т. п. В физике и других науках, использующих математический аппарат, применяются символические имена для обозначения величин. Чтобы не терялся смысл, для определенных величин используются стандартные имена. Например, время обозначают буквой t скорость — V, силу — F и так далее.
Если значение величины не изменяется, то она называется постоянной величиной или константой. Пример константы — число Пифагора n =З,14159... Величина, меняющая свое значение, называется переменной.
Например, в описании процесса падения тела переменными величинами являются высота (Н) и время падения (t).
Третьим свойством величины является ее тип. С понятием типа величине вы также встречались в базах данных. Тип определяет мужество значений, которые может принимать величина. Основные типы величин: числовой, символьный, логический. Поскольку в данном разделе мы будем говорить лишь о количественных характеристиках, то и рассматриваться будут только величины числового типа.
А теперь вернемся к приведенным в начале параграфа примерам 1-3 и обозначим (поименуем) все переменные величины, зависимости между которыми нас будут интересовать. Кроме имен укажем размерности величин.
Размерности определяют единицы, в которых представляются значения величин:
1) t (сек) — время падения; Н (ж) — высота падения. Зависимость будем представлять, пренебрегая учетом сопротивления воздуха. Ускорение свободного падения g (м/сек2) — константа.
2) Р (кг/м2) — давление газа; t°С — температура газа. Давление при нуле градусов Р0 считается константой для данного газа.
3) Загрязненность воздуха будем характеризовать концентрацией примесей (каких именно, будет сказано позже) — С(мг/куб. м).
Единица измерения — масса примесей, содержащихся в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости будем характеризовать числом хронических больных астмой, приходящимся на 1000 жителей данного города — Р (бол./тыс).
Если зависимое между величинами удается представить в математической форме, то мы имеем математическую модель.
Математическая модель - это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики.
Хорошо известны математические модели для первых двух примеров из перечисленных выше. Они отражают физические законы и представляются в виде формул:
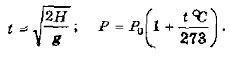
Это примеры зависимостей, представленных в функции пильной форме. Первую зависимость называют корневой (время пропорционально квадратному корню от высоты), вторую — линейной (давление прямо пропорционально температуре).
В более сложных задачах математические модели представляются в виде уравнений или систем уравнений. В этом случае для извлечения функциональной зависимости величин нужно уметь решать эти уравнения. В конце данной главы будет рассмотрен пример математической модели, которая выражается системой неравенств.
Рассмотрим примеры двух других способов представления зависимостей между величинами: табличного и графического.
Представьте себе, что мы решили проверить закон свободного падения тела экспериментальным путем. Эксперимент организовали следующим образом; бросаем стальной шарик с балкона 2-го этажа, 3-го этажа (и так далее) десятиэтажного дома, замеряя высоту начального положения шарика и время падения. По результатам эксперимента мы составили таблицу и нарисовали график.
 ' '
Рис. 2.11. Табличное и графическое представление зависимости времени падения тела от высоты
Если каждую пару значений Н и t из данной таблицы подставить в приведенную выше формулу зависимости высоты от времени, то она превратится в равенство (с точностью до погрешности измерений). Значит, модель работает хорошо. (Однако если сбрасывать не стальной шарик, а большой легкий мяч, то данная модель будет меньше соответствовать формуле, а если надувной шарик, то совсем не будет соответствовать — как вы думаете, почему?)
В этом примере мы рассмотрели три способа отображения зависимости величин: функциональный (формула), табличный и графический. Однако математической моделью процесса падения тела на землю можно назвать только формулу. Почему? Потому что формула универсальна. Она позволяет определить время падения тела с любой высоты, а не только для того экспериментального набора значений Н, который отображен на рис. 2.11.
Кроме того, таблица и диаграмма (график) констатируют факты, а математическая модель позволяет прогнозировать, предсказывать путем расчетов .
Точно так же тремя способами можно отобразить зависимость давления от температуры. Оба примера связаны с известными физическими законами — законами природы. Знания физических законов позволяют производить точные расчеты, они лежит в основе современной техники.
Коротко о главном
Величина — некоторая количественная характеристика объекта.
Зависимости между величинами могут быть представлены в виде математической модели, в табличной и графической формах.
Зависимость, представленная в виде формулы, является математической моделью.
Вопросы и задания
1. а) Какие вам известны формы представления зависимостей между величинами?
б) Что такое математическая модель?
в) Может ли математическая модель включать в себя только константы?
2. Приведите пример известной вам функциональной зависимости (формулы) между характеристиками некоторой системы.
3. Обоснуйте преимущества и недостатки каждой из трех форм представления зависимостей.
Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|