|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| | + | <metakeywords>Информатика, класc, урок, на тему, 11 класc, Корреляционные зависимости</metakeywords> |
| | + | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: Корреляционные зависимости ''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: Корреляционные зависимости ''' |
| | | | |
| - | '''<metakeywords>Корреляционные зависимости</metakeywords>''' <br> ''' Корреляционные зависимости''' <br>
| + | <br> <br> '''Корреляционные зависимости''' <br> |
| | | | |
| - | '' Регрессионные математические модели строятся в тех случаях, когда известно, что зависимость между двумя факторами существует и требуется получить ее математическое описание. А сейчас мы рассмотрим задачи другого рода. Пусть важной характеристикой некоторой сложной системы является фактор А. На него могут оказывать влияние одновременно многие другие факторы: B, С, D и так далее.''<br>
| + | <br> |
| | | | |
| - | '' Мы рассмотрим два типа задач — требуется определить:''<br> | + | '''[[Построение регрессионных моделей с помощью табличного профессора|Регрессионные]]''' математические модели строятся в тех случаях, когда известно, что зависимость между двумя факторами существует и требуется получить ее математическое описание. А сейчас мы рассмотрим задачи другого рода. Пусть важной характеристикой некоторой сложной системы является фактор А. На него могут оказывать влияние одновременно многие другие факторы: B, С, D и так далее.<br> |
| | | | |
| - | '' 1) оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А;''<br>
| + | Мы рассмотрим два типа задач — требуется определить:<br> |
| | | | |
| - | '' 2) какие из факторов В, С, D и так далее оказывают наибольшее влияние на фактор А;''<br>
| + | 1) оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А;<br> |
| | | | |
| - | '' В качестве примера сложной системы будем рассматривать школу. Пусть для первого типа задач фактором А является средняя успеваемость учащихся школы, фактором В — финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п. ''<br>
| + | 2) какие из факторов В, С, D и так далее оказывают наибольшее влияние на фактор А;<br> |
| | | | |
| - | '' Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие причины: уровень квалификации учителей, контингент учащихся, уровень технических средств обучения и другие.''<br>
| + | В качестве примера сложной системы будем рассматривать школу. Пусть для первого типа задач фактором А является средняя успеваемость учащихся школы, фактором В — финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п. <br> |
| | | | |
| - | '' Специалисты по статистике знают, что, для того чтобы выявить зависимость от какого-то определенного фактора, нужно максимально исключить влияние других факторов. Проще говоря, собирая информацию из разных школ, нужно выбирать такие школы, в которых приблизительно одинаковый контингент учеников, квалификация учителей и пр., но хозяйственные расходы школ разные (у одних школ могут быть богатые спонсоры, у других — нет).''<br>
| + | Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие причины: уровень [http://xvatit.com/vuzi/ '''квалификации учителей'''], контингент учащихся, уровень технических средств обучения и другие.<br> |
| | | | |
| - | '' Итак, пусть хозяйственные расходы школы выражаются количеством рублей, отнесенных к числу учеников в школе (руб/чел.), потраченных за определенный период времени (например, за последние 5 лет). Успеваемость же пусть оценивается средним баллам учеников школы по результатам окончания последнего учебного года. Еще раз обращаем ваше внимание на то, что в статистических расчетах обычно используются относительные и усредненные величины.'' | + | Специалисты по статистике знают, что, для того чтобы выявить зависимость от какого-то определенного фактора, нужно максимально исключить влияние других факторов. Проще говоря, собирая '''[[Поиск информации в Интернете|информацию]]''' из разных школ, нужно выбирать такие школы, в которых приблизительно одинаковый контингент учеников, квалификация учителей и пр., но хозяйственные расходы школ разные (у одних школ могут быть богатые спонсоры, у других — нет).<br> |
| | | | |
| - | '' Итоги сбора данных по 20 школам, введенные в электронную таблицу, представлены на рис. 2.16. На рис. 2.17 приведена точечная диаграмма, построенная по этим данным.''
| + | Итак, пусть хозяйственные расходы школы выражаются количеством рублей, отнесенных к числу учеников в школе (руб/чел.), потраченных за определенный период времени (например, за последние 5 лет). Успеваемость же пусть оценивается средним баллам учеников школы по результатам окончания последнего учебного года. Еще раз обращаем ваше внимание на то, что в статистических расчетах обычно используются относительные и усредненные величины. |
| | | | |
| - | <br> '' [[Image:Инф102.jpg]]''
| + | Итоги сбора данных по 20 школам, введенные в '''[[Электронные таблицы|электронную таблицу]]''', представлены на рис. 2.16. На рис. 2.17 приведена точечная диаграмма, построенная по этим данным. |
| | | | |
| - | ''<br> Рис. 2.16 Статистические данные'' | + | <br> '' [[Image:Инф102.jpg|320px|Статистические данные]]''''<br>''' Рис. 2.16 Статистические данные'' |
| | | | |
| - | ''<br> <br> [[Image:Инф103.jpg]]'' | + | ''<br> [[Image:Инф103.jpg|320px|Точечная диаграмма]]''''<br> ''' Рис. 2.17. Точечная диаграмма'' |
| | | | |
| - | ''<br> Рис. 2.17. Точечная диаграмма'' | + | ''<br>''Значения обеих величин: финансовых затрат и успеваемости учеников имеют значительный разброс и, на первый взгляд, взаимосвязи между ними не видно. Однако она вполне может существовать. |
| | | | |
| - | ''<br> Значения обеих величин: финансовых затрат и успеваемости учеников имеют значительный разброс и, на первый взгляд, взаимосвязи между ними не видно. Однако она вполне может существовать.''
| + | Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями. |
| | | | |
| - | '' Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются '''корреляционными зависимостями'''.''
| + | Раздел математической статистики, который исследует такие зависимости, называется корреляционным анализом. |
| | | | |
| - | '' Раздел математической статистики, который исследует такие зависимости, называется '''корреляционным анализом'''. ''
| + | Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости. |
| | | | |
| - | '' Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости.''
| + | Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Чаще всего допускают наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции. |
| | | | |
| - | '' Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Чаще всего допускают наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции. ''
| + | Как и прежде, мы не будем писать формулы, по которым он вычисляется; их написать нетрудно, гораздо труднее понять, почему они именно такие. На данном этапе вам достаточно знать следующее: |
| | | | |
| - | '' Как и прежде, мы не будем писать формулы, по которым он вычисляется; их написать нетрудно, гораздо труднее понять, почему они именно такие. На данном этапе вам достаточно знать следующее:''
| + | • коэффициент корреляции (обычно обозначаемый греческой буквой р) есть число, заключенное в диапазоне от -1 до +1; |
| | | | |
| - | '' • коэффициент корреляции (обычно обозначаемый греческой буквой р) есть число, заключенное в диапазоне от -1 до +1;''
| + | • если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая; |
| | | | |
| - | '' • если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая;''
| + | • близость р к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное; |
| | | | |
| - | '' • близость р к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное;''
| + | • значение р легко найти с помощью Excel без всяких формул (разумеется, потому, что в Excel они встроены). |
| | | | |
| - | '' • значение р легко найти с помощью Excel без всяких формул (разумеется, потому, что в Excel они встроены).''
| + | В Excel функция вычисления коэффициента корреляции называется КОРРЕЛ и входит е группу статистических функций. Покажем, как ей воспользоваться. |
| | | | |
| - | '' В Excel функция вычисления коэффициента корреляции называется КОРРЕЛ и входит е группу статистических функций. Покажем, как ей воспользоваться.''
| + | На том же листе Excel, где находится таблица, представленная на рис. 2.16, надо установить курсор на любую свободную ячейку и запустить функцию КОРРЕЛ. Она запросит два диапазона значений. Укажем В2:В21 и С2:С21. После их ввода выведется ответ: р = 0,500273843. Эта величина говорит о среднем уровне корреляции. |
| | | | |
| - | '' На том же листе Excel, где находится таблица, представленная на рис. 2.16, надо установить курсор на любую свободную ячейку и запустить функцию КОРРЕЛ. Она запросит два диапазона значений. Укажем В2:В21 и С2:С21. После их ввода выведется ответ: р = 0,500273843. Эта величина говорит о среднем уровне корреляции.''
| + | Наличие зависимости между хозяйственными затратами школы и успеваемостью нетрудно понять. Ученики с удовольствием ходят в чистую, красивую, уютную школу, чувствуют там себя как дома и поэтому лучше учатся. |
| | | | |
| - | '' Наличие зависимости между хозяйственными затратами школы и успеваемостью нетрудно понять. Ученики с удовольствием ходят в чистую, красивую, уютную школу, чувствуют там себя как дома и поэтому лучше учатся.''
| + | В следующем примере проводится исследование по определению зависимости успеваемости учащихся старших классов от двух факторов: обеспеченности школьной библиотеки учебниками и обеспеченности школы компьютерами. И та и другая характеристика количественно выражаются в процентах от нормы. |
| | | | |
| - | '' В следующем примере проводится исследование по определению зависимости успеваемости учащихся старших классов от двух факторов: обеспеченности школьной библиотеки учебниками и обеспеченности школы компьютерами. И та и другая характеристика количественно выражаются в процентах от нормы. ''
| + | Нормой обеспеченности учебниками является их полный комплект, то есть такое количество, когда каждому ученику выдаются из библиотеки все нужные ему для учебы книги. Нормой обеспеченности компьютерами будем считать такое их количество, при котором на каждые четыре старшеклассника в школе приходится один компьютер. Предполагается, что компьютерами ученики пользуются не только на информатике, но и на других уроках, а также во внеурочное время. |
| | | | |
| - | '' Нормой обеспеченности учебниками является их полный комплект, то есть такое количество, когда каждому ученику выдаются из библиотеки все нужные ему для учебы книги. Нормой обеспеченности компьютерами будем считать такое их количество, при котором на каждые четыре старшеклассника в школе приходится один компьютер. Предполагается, что компьютерами ученики пользуются не только на информатике, но и на других уроках, а также во внеурочное время.'' | + | ''<br> [[Image:Инф104.jpg|480px|Сравнение двух корреляционных зависимостей]]'' |
| | | | |
| - | '' В таблице, изображенной на рис. 2.18, приведены результаты измерения обоих факторов в 11 разных школах. Напомним, что влияние каждого фактора исследуется независимо от других (то есть влияние других существенных факторов должно быть приблизительно одинаковым).<br> [[Image:Инф104.jpg]]'' | + | '' Рис.2.18. Сравнение двух'' ''корреляционных зависимостей<br>'' |
| | | | |
| - | '' Рис.2.18. Сравнение двух'' ''корреляционных зависимостей<br>''
| + | <br>Для обеих зависимостей получены коэффициенты линейной корреляции. Как видно из таблицы, корреляция между обеспеченностью учебниками и успеваемостью сильнее, чем корреляция между компьютерным обеспечением и успеваемостью (хотя и тот и другой коэффициенты корреляции не очень большие). Отсюда можно сделать вывод, что пока еще книга остается более значительным источником знаний, чем компьютер.<br><br>'''Коротко о главном'''<br><br>Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными. |
| | | | |
| - | ''<br> Для обеих зависимостей получены коэффициенты линейной корреляции. Как видно из таблицы, корреляция между обеспеченностью учебниками и успеваемостью сильнее, чем корреляция между компьютерным обеспечением и успеваемостью (хотя и тот и другой коэффициенты корреляции не очень большие). Отсюда можно сделать вывод, что пока еще книга остается более значительным источником знаний, чем компьютер.<br><br><br> '''Коротко о главном'''<br><br><br> Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются '''корреляционными'''.''
| + | С помощью корреляционного анализа можно решить следующие задачи: определить, оказывает ли один фактор существенное влияние на другой фактор; из нескольких факторов выбрать наиболее существенный. |
| | | | |
| - | '' С помощью корреляционного анализа можно решить следующие задачи: определить, оказывает ли один фактор существенное влияние на другой фактор; из нескольких факторов выбрать наиболее существенный.''
| + | Количественной мерой корреляции двух величин является коэффициент корреляции. |
| | | | |
| - | '' Количественной мерой корреляции двух величин является коэффициент корреляции.''
| + | Значение коэффициента корреляции лежит между -1 и +1. Чем ближе его значение по модулю к 1, тем корреляция (связь) сильнее. |
| | | | |
| - | '' Значение коэффициента корреляции лежит между -1 и +1. Чем ближе его значение по модулю к 1, тем корреляция (связь) сильнее.<br>В MS Excel для определения коэффициента корреляции используется функция КОРРЕЛ из группы статистических функций.<br><br><br> '''Вопросы и задания'''<br><br><br> 1.а) Что такое корреляционная зависимость?''
| + | В MS Excel для определения коэффициента корреляции используется функция КОРРЕЛ из группы статистических функций.<br><br>'''Вопросы и задания'''''<br><br>1.а) Что такое корреляционная зависимость?'' |
| | | | |
| - | '' б) Что такое корреляционный анализ?'' | + | ''б) Что такое корреляционный анализ?'' |
| | | | |
| - | '' в) Какие типы задач можно решать с помощью корреляционного анализа?'' | + | ''в) Какие типы задач можно решать с помощью корреляционного анализа?'' |
| | | | |
| - | '' г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?'' | + | ''г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?'' |
| | | | |
| - | '' 2. С помощью какого средствд табличного процессора можно вычислить коэффициент корреляции?'' | + | ''2. С помощью какого средствд табличного процессора можно вычислить коэффициент корреляции?'' |
| | | | |
| - | '' 3. а) Для данных из таблицы, представленной на рис. 2.18. постройте две линейные регрессионные модели.'' | + | ''3. а) Для данных из таблицы, представленной на рис. 2.18. постройте две линейные регрессионные модели.'' |
| | | | |
| - | '' 6) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.'''''<br>'''<br> | + | ''6) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.'' |
| | + | |
| | + | '''<br>'''<br> |
| | | | |
| | ''Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11'' | | ''Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11'' |
| Строка 90: |
Строка 94: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 06:11, 7 июля 2012
Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: Корреляционные зависимости
Корреляционные зависимости
Регрессионные математические модели строятся в тех случаях, когда известно, что зависимость между двумя факторами существует и требуется получить ее математическое описание. А сейчас мы рассмотрим задачи другого рода. Пусть важной характеристикой некоторой сложной системы является фактор А. На него могут оказывать влияние одновременно многие другие факторы: B, С, D и так далее.
Мы рассмотрим два типа задач — требуется определить:
1) оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А;
2) какие из факторов В, С, D и так далее оказывают наибольшее влияние на фактор А;
В качестве примера сложной системы будем рассматривать школу. Пусть для первого типа задач фактором А является средняя успеваемость учащихся школы, фактором В — финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п.
Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие причины: уровень квалификации учителей, контингент учащихся, уровень технических средств обучения и другие.
Специалисты по статистике знают, что, для того чтобы выявить зависимость от какого-то определенного фактора, нужно максимально исключить влияние других факторов. Проще говоря, собирая информацию из разных школ, нужно выбирать такие школы, в которых приблизительно одинаковый контингент учеников, квалификация учителей и пр., но хозяйственные расходы школ разные (у одних школ могут быть богатые спонсоры, у других — нет).
Итак, пусть хозяйственные расходы школы выражаются количеством рублей, отнесенных к числу учеников в школе (руб/чел.), потраченных за определенный период времени (например, за последние 5 лет). Успеваемость же пусть оценивается средним баллам учеников школы по результатам окончания последнего учебного года. Еще раз обращаем ваше внимание на то, что в статистических расчетах обычно используются относительные и усредненные величины.
Итоги сбора данных по 20 школам, введенные в электронную таблицу, представлены на рис. 2.16. На рис. 2.17 приведена точечная диаграмма, построенная по этим данным.
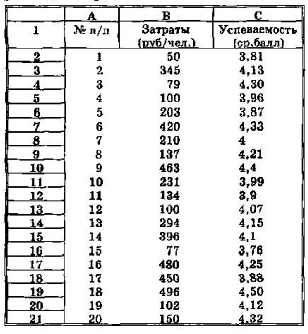 ' '
Рис. 2.16 Статистические данные
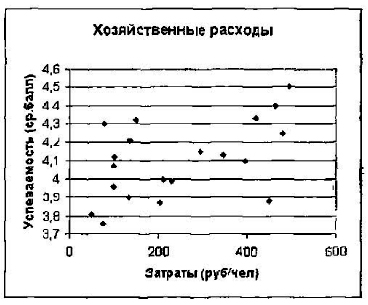 ' '
Рис. 2.17. Точечная диаграмма
Значения обеих величин: финансовых затрат и успеваемости учеников имеют значительный разброс и, на первый взгляд, взаимосвязи между ними не видно. Однако она вполне может существовать.
Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями.
Раздел математической статистики, который исследует такие зависимости, называется корреляционным анализом.
Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости.
Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Чаще всего допускают наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции.
Как и прежде, мы не будем писать формулы, по которым он вычисляется; их написать нетрудно, гораздо труднее понять, почему они именно такие. На данном этапе вам достаточно знать следующее:
• коэффициент корреляции (обычно обозначаемый греческой буквой р) есть число, заключенное в диапазоне от -1 до +1;
• если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая;
• близость р к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное;
• значение р легко найти с помощью Excel без всяких формул (разумеется, потому, что в Excel они встроены).
В Excel функция вычисления коэффициента корреляции называется КОРРЕЛ и входит е группу статистических функций. Покажем, как ей воспользоваться.
На том же листе Excel, где находится таблица, представленная на рис. 2.16, надо установить курсор на любую свободную ячейку и запустить функцию КОРРЕЛ. Она запросит два диапазона значений. Укажем В2:В21 и С2:С21. После их ввода выведется ответ: р = 0,500273843. Эта величина говорит о среднем уровне корреляции.
Наличие зависимости между хозяйственными затратами школы и успеваемостью нетрудно понять. Ученики с удовольствием ходят в чистую, красивую, уютную школу, чувствуют там себя как дома и поэтому лучше учатся.
В следующем примере проводится исследование по определению зависимости успеваемости учащихся старших классов от двух факторов: обеспеченности школьной библиотеки учебниками и обеспеченности школы компьютерами. И та и другая характеристика количественно выражаются в процентах от нормы.
Нормой обеспеченности учебниками является их полный комплект, то есть такое количество, когда каждому ученику выдаются из библиотеки все нужные ему для учебы книги. Нормой обеспеченности компьютерами будем считать такое их количество, при котором на каждые четыре старшеклассника в школе приходится один компьютер. Предполагается, что компьютерами ученики пользуются не только на информатике, но и на других уроках, а также во внеурочное время.
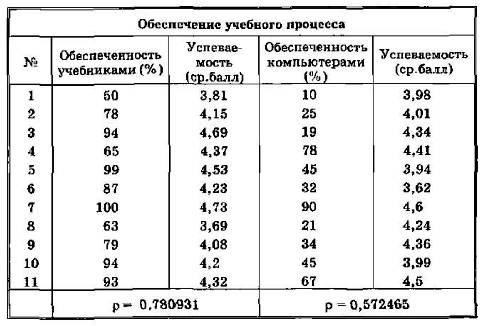
Рис.2.18. Сравнение двух корреляционных зависимостей
Для обеих зависимостей получены коэффициенты линейной корреляции. Как видно из таблицы, корреляция между обеспеченностью учебниками и успеваемостью сильнее, чем корреляция между компьютерным обеспечением и успеваемостью (хотя и тот и другой коэффициенты корреляции не очень большие). Отсюда можно сделать вывод, что пока еще книга остается более значительным источником знаний, чем компьютер.
Коротко о главном
Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными.
С помощью корреляционного анализа можно решить следующие задачи: определить, оказывает ли один фактор существенное влияние на другой фактор; из нескольких факторов выбрать наиболее существенный.
Количественной мерой корреляции двух величин является коэффициент корреляции.
Значение коэффициента корреляции лежит между -1 и +1. Чем ближе его значение по модулю к 1, тем корреляция (связь) сильнее.
В MS Excel для определения коэффициента корреляции используется функция КОРРЕЛ из группы статистических функций.
Вопросы и задания
1.а) Что такое корреляционная зависимость?
б) Что такое корреляционный анализ?
в) Какие типы задач можно решать с помощью корреляционного анализа?
г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?
2. С помощью какого средствд табличного процессора можно вычислить коэффициент корреляции?
3. а) Для данных из таблицы, представленной на рис. 2.18. постройте две линейные регрессионные модели.
6) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.
Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













