|
|
|
| (8 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: Использование MS Excel для решения задачи оптимального планирования ''' ''<br><metakeywords>Использование MS Excel для решения задачи оптимального планирования</metakeywords>'' | + | <metakeywords>Информатика, класc, урок, на тему, 11 класc, Использование MS Excel для решения задачи оптимального планирования, электронная таблица, алгоритм</metakeywords> |
| | + | |
| | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: Использование MS Excel для решения задачи оптимального планирования ''' |
| | | | |
| | <br> | | <br> |
| | | | |
| - | ''' Использование MS Excel для решения задачи оптимального планирования ''' ''<br>'' | + | '''Использование MS Excel для решения задачи оптимального планирования ''' ''<br>'' |
| | | | |
| - | <br> '' В математическом программировании существуют свои сложные методы решения задач. Их изучение не входит в наши планы. Поступим так же, как поступали и раньше — воспользуемся тем, что в программу Excel возможности решения задач математического программирования заложены и можно находить решение, не владея его механизмом.'' | + | <br> В математическом программировании существуют свои сложные методы решения задач. Их изучение не входит в наши планы. Поступим так же, как поступали и раньше — воспользуемся тем, что в программу '''[[Мастер диаграмм в табличном процессоре MS Excel|Excel]]''' возможности решения задач математического программирования заложены и можно находить решение, не владея его механизмом. |
| | | | |
| - | '' Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («пирожки и пирожные»), как воспользоваться указанным средством.''
| + | Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («пирожки и пирожные»), как воспользоваться указанным средством. |
| | | | |
| - | '' Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х (план по изготовлению пирожков) и у (план по изготовлению пирожных). Ниже этих ячеек представлена система неравенств [[Image:Инф106.jpg|23x21px]]''''', '''''определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция'[[Image:Инф107.jpg]] занесена в ячейку В15.'''''<br> [[Image:Инф110.jpg]]'''
| + | Вначале надо подготовить '''[[Электронные таблицы|электронную таблицу]]''' к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х (план по изготовлению пирожков) и у (план по изготовлению пирожных). Ниже этих ячеек представлена система неравенств [[Image:Инф106.jpg|23x21px|Инф106.jpg]]''''','''''определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция'[[Image:Инф107.jpg]] занесена в ячейку В15.'''''<br> [[Image:Инф110.jpg|480px|Таблица]]''''''<br>''''' '''''<i>Рис. 2.20. Таблица, подготовленная к вычислению оптимального плана</i> |
| | | | |
| - | '''<br>''''' Рис. 2.20. Таблица, подготовленная к вычислению оптимального плана'' | + | Теперь следует вызвать [http://xvatit.com/it/fishki-ot-itshki/ '''программу'''] оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма (рис. 2.21). |
| | | | |
| - | '' Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма (рис. 2.21).<br>[[Image:инф111.jpg]]<br>Рис. 2.21. Начальное состояние формы "Поиск решения»<br>Далее надо выполнить следующий алгоритм;<br>1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим устано¬вить курсор на ячейку В15, то ввод произойдет автомати¬чески).<br>2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.<br>3. В поле «Изменяя ячейки» ввести В5:С5, то есть сооб¬щать, какое место отведено под значения переменных -плановых показателей.<br>4. В поле «Ограничения» надо ввести информацию о нера¬венствах-ограничениях, которые имеют вид B10<=D10; B11<HD11; В12>=Ш2; В13>=ШЗ. Ограничения вводят¬ся следующим образом:<br>^> щелкнуть по кнопке «Добавить»;<br>в появившемся диалоговом окне «Добавление ограниче¬ния» ввести ссылку на ячейку В10, выбрать из меню знак неравенства <=* и ввести ссылку на ячейку ШО; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11<=D11 и так далее. В конце надо щелкнуть по кнопке ОК.<br>Пчмпк р<br>Восстэкеип,<br>5. Закрыть диалоговое окно «Добавление ограничения».<br>Снова появится форма «Поиск решения» (рис. 2.22).<br> <br><br>|*0|5:$С$5 3J Пр*ДПОЛО£ИТЬ |<br><br> <br><br> <br> <br><br> <br> <br><br><br><br><br>Рис. 2.22. Форма «Поиск решения» после ввода информации<br> <br>Математическое моделирование в планировании и управлении:<br> <br>133<br> <br><br><br>6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее реше¬ние). Для этого следует щелкнуть по кнопке «Парамет¬ры* — появится форма «Параметры поиска решения» (рис. 2.23).<br> <br>Подомни* 1У>исхл г***«<br> <br><br>а*}<br> <br><br> <br>Максимальное время: 11 СЮ секунд<br>Предельное *»кло итераций: ) 100<br> <br><br>ПК<br><br>От немо<br> <br>Относительная погрешность: |o,COCOGl<br>Дргтустииое отктюн?***: ]5~~<br>Сходипость: ДОЮ<br> <br><br><br><br>%<br> <br>Загрузить модель... Сохранить модель...<br> <br><br> <br>Р гьщеЛея модель<br> <br>" Автоматическое масштабах»».*»*;<br> <br>Г" Неотрицетвльнув значения Г" Показывать результаты итераций<br> <br>Оценки <br>(• линоииая<br>С квадратичная<br>Г<br>Ра>юсти<br><br>црнгрюные<br> <br>Метод поиска -&*>тона f сопряженных градиентов<br> <br><br><br>Рис. 2.23. Форма «Параметры поиска решения»<br>7. Надо выставить флажок на переключателе «Линейная модель». Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавли¬ваемые значения нас устраивают, и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что воз¬вратит нас в форму «Поиск решения».<br>8. Вся информация введена. Далее надо щелкнуть по кноп¬ке «Выполнить» — мгновенно в ячейках В5 и С5 появит¬ся оптимальное решение (числа 600 и 100), а также число 800 в ячейке В15 — максимальное значение целевой функции (рис. 2.24).<br> <br> A В С D<br>1 Оптимальное плаакронанке <br>2 <br>3 Плановые показатели <br>4 X (пирожки) Y (пирожные) <br>5 600 100 <br> <br>7 Ограничения <br>8 <br>9 Левая часть Знак Правая наешь<br>10 Время<br>производства: 1000 1000<br>11 Общее количество: 700 <= 700<br>12 Положительность X: 600 >~ 0<br>13 Положительность У: 100 >«= 0<br>14 <br>15 Целевая функция 800 <br>j 16_ <br><br><br><br>Кроме того, на экране появилась еще одна форма — «Ре¬зультаты поиска решения» (рис, 2.25).<br>На первом этапе освоения возможностей программы на эту форму можно не обращать внимания (хотя в принципе в ней может оказаться очень полезная информация).<br>Итак, в результате применения инструмента «Поиск ре¬шения», мы получим следующий оптимальный план днев¬ного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют положешю точки В на рис- 2.19. В этой точ¬ке значение целевой функции /(600,100) = 800. Если один пирожок стоит 2 рубля, то полученная выручка составит 1600 рублей.<br>Решение, которое мы получили, вполне разумно как с экономической точки зрения, так и с медицинской. Много сладкого — вредно для здоровья, а пирожки и сытнее, и по¬лезнее.<br>Полученная электронная таблица и настроенная на нее сервисная функция «Поиск решения» являются средством, с помощью которого можно решать задачу оптимального планирования при меняющихся условиях. Например, мо¬жет измениться длина рабочего дня. Тогда надо внести но¬вое значение в ячейку Ш0, и оптимальный план автомати¬чески пересчитается. Также может измениться допустимое суммарное число изделий в ячейке D11.<br>Представьте себе, что в вашей школе учатся неисправи¬мые сладкоежки. И, кроме всех прочих ограничений, перед кондитерским цехом ставится обязательное условие; число пирожных должно быть не меньше числа пирожков. При та¬кой постановке задачи система неравенств (а) примет вид:<br>[* + 4у i 1000; х + у \ 700;<br>pics<br>У ] £•<br>Соответствующее изменение легко внести в электронную таблицу. Для этого достаточно в ячейке ШЗ вместо 0 запи¬сать В5. Результаты поиска решения будут следующими: х = 200, у = 200, f{xty) = 600. Таким планом вряд ли будет? доволен директор кондитерского цеха, поскольку потери прибыли окажутся очень существенными.<br>Следует иметь в виду, что при решении подобных зада** могут возникнуть проблемы, о которых мы здесь не говори¬ли. Например, искомого оптимального решения может вовсе не существовать — тогда программа об этом сообщит. Одна ко мы не ставили перед собой цели детально разобраться в задачах оптимального планирования и методах математи¬ческого программирования. Достаточно того, что вы позна¬комились с постановкой таких задач и с компьютерными средствами для их решения.<br>'''''<br> ''''''Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11''''' '''
| + | ''<br> [[Image:Инф111.jpg|480px|Начальное состояние формы «Поиск решения»]]''''<br> ''' Рис. 2.21. Начальное состояние формы «Поиск решения»'' |
| | + | |
| | + | ''<br>''Далее надо выполнить следующий '''[[Что такое алгоритм|алгоритм]]''': |
| | + | |
| | + | 1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически). |
| | + | |
| | + | 2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции. |
| | + | |
| | + | 3. В поле «Изменяя ячейки» ввести В5:С5, то есть сообщать, какое место отведено под значения переменных плановых показателей. |
| | + | |
| | + | 4. В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10<=D10; B11<=D11; В12>=D12; В13>=D1З. Ограничения вводятся следующим образом: |
| | + | |
| | + | => щелкнуть по кнопке «Добавить»; |
| | + | |
| | + | в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11<=D11 и так далее. В конце надо щелкнуть по кнопке ОК. |
| | + | |
| | + | 5. Закрыть диалоговое окно «Добавление ограничения».<br>Снова появится форма «Поиск решения» (рис. 2.22).''<br> <br>[[Image:Инф112.jpg|480px|Форма «Поиск решения» после ввода информации]]<br> Рис. 2.22. Форма «Поиск решения» после ввода информации<br> <br>''6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры»— появится форма «Параметры поиска решения» (рис. 2.23).''<br> <br>[[Image:Инф113.jpg|480px|Форма «Параметры поиска решения»]]''''<br> ''' Рис. 2.23. Форма «Параметры поиска решения»'' |
| | + | |
| | + | <br> 7. Надо выставить флажок на переключателе «Линейная модель». Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают, и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения». |
| | + | |
| | + | 8. Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 600 и 100), а также число 800 в ячейке В15 — максимальное значение целевой функции (рис. 2.24).''<br> <br>[[Image:Инф114.jpg|480px|Результаты решения задачи]]<br> Рис.2.24. Результаты решения задачи'' |
| | + | |
| | + | ''<br>''Кроме того, на экране появилась еще одна форма — «Результаты поиска решения» (рис. 2.25). |
| | + | |
| | + | На первом этапе освоения возможностей программы на эту форму можно не обращать внимания (хотя в принципе в ней может оказаться очень полезная информация). |
| | + | |
| | + | Итак, в результате применения инструмента «Поиск решения», мы получим следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют положению точки В на рис. 2.19. В этой точке значение целевой функции f(600,100) = 800. Если один пирожок стоит 2 рубля, то полученная выручка составит 1600 рублей. |
| | + | |
| | + | Решение, которое мы получили, вполне разумно как с экономической точки зрения, так и с медицинской. Много сладкого — вредно для здоровья, а пирожки и сытнее, и полезнее. |
| | + | |
| | + | Полученная электронная таблица и настроенная на нее сервисная функция «Поиск решения» являются средством, с помощью которого можно решать задачу оптимального планирования при меняющихся условиях. Например, может измениться длина рабочего дня. Тогда надо внести новое значение в ячейку D10, и оптимальный план автоматически пересчитается. Также может измениться допустимое суммарное число изделий в ячейке D11. |
| | + | |
| | + | Представьте себе, что в вашей школе учатся неисправимые сладкоежки. И, кроме всех прочих ограничений, перед кондитерским цехом ставится обязательное условие; число пирожных должно быть не меньше числа пирожков. При такой постановке задачи система неравенств [[Image:Инф106.jpg]] примет вид: |
| | + | |
| | + | х + 4у i 1000; |
| | + | |
| | + | х + у j 700; |
| | + | |
| | + | х j 0 |
| | + | |
| | + | у j х. |
| | + | |
| | + | Соответствующее изменение легко внести в электронную таблицу. Для этого достаточно в ячейке D1З вместо 0 записать В5. Результаты поиска решения будут следующими: х = 200, у = 200, f{x,y) = 600. Таким планом вряд ли будет? доволен директор кондитерского цеха, поскольку потери прибыли окажутся очень существенными. |
| | + | |
| | + | <br> |
| | + | |
| | + | ''<br>'''''<br> '''''Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11'' |
| | | | |
| | ''Отослано читателями из интернет-сайтов''<br><br> | | ''Отослано читателями из интернет-сайтов''<br><br> |
| Строка 20: |
Строка 68: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 06:54, 7 июля 2012
Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: Использование MS Excel для решения задачи оптимального планирования
Использование MS Excel для решения задачи оптимального планирования
В математическом программировании существуют свои сложные методы решения задач. Их изучение не входит в наши планы. Поступим так же, как поступали и раньше — воспользуемся тем, что в программу Excel возможности решения задач математического программирования заложены и можно находить решение, не владея его механизмом.
Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («пирожки и пирожные»), как воспользоваться указанным средством.
Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х (план по изготовлению пирожков) и у (план по изготовлению пирожных). Ниже этих ячеек представлена система неравенств 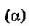 ,определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция' ,определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция'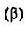 занесена в ячейку В15. занесена в ячейку В15.
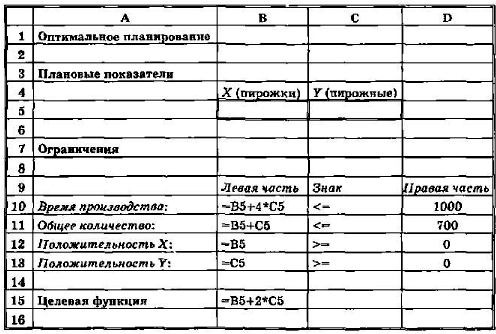 ' '
Рис. 2.20. Таблица, подготовленная к вычислению оптимального плана
Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма (рис. 2.21).
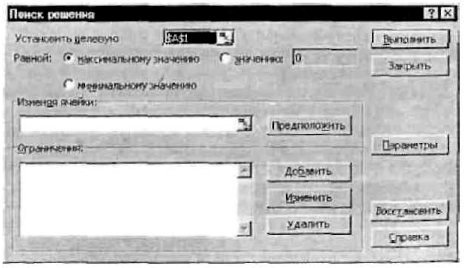 ' '
Рис. 2.21. Начальное состояние формы «Поиск решения»
Далее надо выполнить следующий алгоритм:
1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).
2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.
3. В поле «Изменяя ячейки» ввести В5:С5, то есть сообщать, какое место отведено под значения переменных плановых показателей.
4. В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10<=D10; B11<=D11; В12>=D12; В13>=D1З. Ограничения вводятся следующим образом:
=> щелкнуть по кнопке «Добавить»;
в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11<=D11 и так далее. В конце надо щелкнуть по кнопке ОК.
5. Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 2.22).
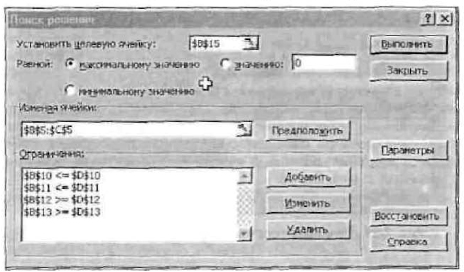
Рис. 2.22. Форма «Поиск решения» после ввода информации
6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры»— появится форма «Параметры поиска решения» (рис. 2.23).
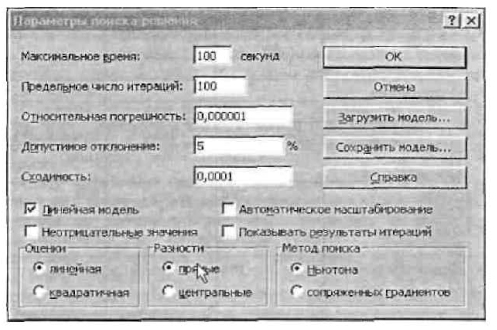 ' '
Рис. 2.23. Форма «Параметры поиска решения»
7. Надо выставить флажок на переключателе «Линейная модель». Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают, и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».
8. Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 600 и 100), а также число 800 в ячейке В15 — максимальное значение целевой функции (рис. 2.24).
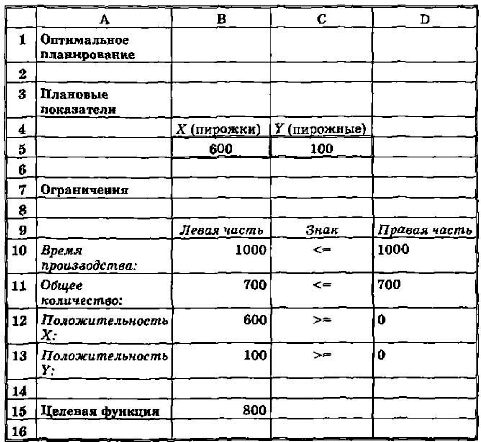
Рис.2.24. Результаты решения задачи
Кроме того, на экране появилась еще одна форма — «Результаты поиска решения» (рис. 2.25).
На первом этапе освоения возможностей программы на эту форму можно не обращать внимания (хотя в принципе в ней может оказаться очень полезная информация).
Итак, в результате применения инструмента «Поиск решения», мы получим следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют положению точки В на рис. 2.19. В этой точке значение целевой функции f(600,100) = 800. Если один пирожок стоит 2 рубля, то полученная выручка составит 1600 рублей.
Решение, которое мы получили, вполне разумно как с экономической точки зрения, так и с медицинской. Много сладкого — вредно для здоровья, а пирожки и сытнее, и полезнее.
Полученная электронная таблица и настроенная на нее сервисная функция «Поиск решения» являются средством, с помощью которого можно решать задачу оптимального планирования при меняющихся условиях. Например, может измениться длина рабочего дня. Тогда надо внести новое значение в ячейку D10, и оптимальный план автоматически пересчитается. Также может измениться допустимое суммарное число изделий в ячейке D11.
Представьте себе, что в вашей школе учатся неисправимые сладкоежки. И, кроме всех прочих ограничений, перед кондитерским цехом ставится обязательное условие; число пирожных должно быть не меньше числа пирожков. При такой постановке задачи система неравенств 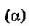 примет вид: примет вид:
х + 4у i 1000;
х + у j 700;
х j 0
у j х.
Соответствующее изменение легко внести в электронную таблицу. Для этого достаточно в ячейке D1З вместо 0 записать В5. Результаты поиска решения будут следующими: х = 200, у = 200, f{x,y) = 600. Таким планом вряд ли будет? доволен директор кондитерского цеха, поскольку потери прибыли окажутся очень существенными.
Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|















