|
|
|
| (2 промежуточные версии не показаны) | | Строка 2: |
Строка 2: |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 4 класс|Математика 4 класс]]>> Урок 20. Из истории дробей''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 4 класс|Математика 4 класс]]>> Урок 20. Из истории дробей''' |
| | + | |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <br>Из истории дробей<br>20 УРОК<br> <br> Потребность в более точных измерениях величин привела к тому, что единицы измерения стали делить на несколько равных частей: 2, 4, 8 и т. д. Каждая часть первоначальной мерки получала свое собственное название. Например, половину в Древней Руси называли еш;е полтиной, о четвертой части говорили — ЧЕТЬ, о восьмой части — ПОЛЧЕТЬ, о шестнадцатой части —ПОЛПОЛЧЕТЬ и т. д. Равные части целой мерки называли долями: четвертые доли, восьмые, шестнадцатые и т. д.<br><br>карт<br><br>Интересная система дробей была в Древнем Риме. Она основывалась на делении древнеримской единицы массы, которая называлась АСС. Асе делили на 12 равных частей. Двенадцатую часть асса называли УНЦИЕЙ. Со временем унции стали применять для измерения других величин. Например, римлянин мог сказать, что он прошел 7 унций пути. При этом речь, конечно, не шла о взвешивании пути. Имелось в виду, что пройдено<br>семь "двенадцатых долей" пути.<br><br>карт<br> <br>Так постепенно происходил переход от конкретных дробей к отвлеченным дробям, не связанным с какой-нибудь определенной мерой.<br><br>карт<br><br>Запись дробей и алгоритмы действий с ними в древности были так сложны, что учение о дробях считалось самым трудным разделом арифметики. Чтобы его освоить, приходилось заучивать огромное число правил действий с дробями. Например, в Древнем Риме в ходу было всего 18 различных дробей: СЕМИС — половина асса, СЕКСТАНС — шестая его доля, СЕСКУНЦИЯ — восьмая, ТРИЕНС — треть асса, БЕС — две трети, СЕМИУНЦИЯ — пол-унции, или одна двадцать четвертая доля асса, и т. д. Чтобы работать с долями, надо было твердо знать, что при сложении ТРИЕНСА и СЕКСТАНСА получается СЕМИС, а при умножении БЕСА на СЕСКУНЦИЮ получается УНЦИЯ. Этих правил было так много, что умение оперировать дробями воспринималось как чудо. Поэтому всегда и везде знание дробей пользовалось особым почетом и уважением. Так, например, автор славянской рукописи XVI века пишет: "Несть се дивно, что в целых, а то похвально, что в долях ..." Об этом же писал в своей знаменитой "Арифметике" русский математик XVIII века Л. Ф. Магницкий:<br><br><br>Но несть тот арифметик. <br>Иже в целых ответчик, <br>А в долях ничтоже <br>Отвеш;ате возможе.<br><br>Тем же о ты радеяй. <br>Буди в частях умеяй.<br><br>карт <br><br>В древности для основных дробей, которые были в обиходе, су-ш;ествовали индивидуальные знаки, а остальные дроби получались из основных дробей с помощью арифметических действий. Вот как, например, обозначались некоторые дроби в Древнем Египте:<br><br>карт<br> <br>Поскольку три четверти составляют в сумме половину и четверть, то эту дробь записывали так:<br><br>карт<br><br>У древних римлян унция обозначалась чертой "—", половина асса, или 6 унций, — S (первой в латинском слове semis — половина). Например, семь двенадцатых записывались так: "S—" <br><br>Современная система записи дробей с числителем и знаменателем была создана в Индии, только там не писали дробной черты. А записывать дробь в точности так, как сейчас, стали арабы. Общеупотребительной эта запись дробей стала лишь в XVI веке.<br><br>карт<br> <br>Старинные задачи с дробями <br><br>1. В произведении знаменитого римского поэта I века до н. э. Горация так описана беседа учителя с учеником в одной из римских п1кол этой эпохи:<br><br>Учитель. Пусть скажет сын Альбина, сколько останется, если от пяти унций отнять одну унцию?<br><br>Ученик. Одна треть.<br><br>Учитель. Правильно. Ты сумеешь беречь свое имугцество.<br><br>Пользуясь схемой, докажи, что ученик был прав:<br> <br>карт<br><br>2. Задача из "Арифметики" известного среднеазиатского математи-ка Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.).<br><br>"Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10".<br><br>карт<br> <br>3. Задача из "Папируса Ахмеса" (Египет, 1850 г. до н. э.), "Приходит пастух с 70 быками. Его спрашивают:<br><br>— Сколько приводишь ты своего многочисленного стада?<br><br>Пастух отвечает:<br><br>— Я привожу две трети от трети скота. Сочти!"<br><br>Используя схему, найди, сколько быков было во всем стаде?<br> <br>карт<br><br><br>70 быков<br> <br>4. Староиндийская задача математика Сриддхары (XI век н. э.).<br> <br>Есть кадамба цветок. <br>На один лепесток <br>Пчелок пятая часть опустилась.<br><br>Рядом тут же росла <br>Вся в цвету сименгда, <br>И на ней третья часть поместилась.<br><br>Разность их ты найди, <br>Ее трижды сложи <br>И тех пчел на кутай посади.<br><br>Только две не нашли <br>Себе место нигде.<br>Все летали то взад, то вперед и везде <br>Ароматом цветов наслаждались.<br><br>Назови теперь мне. <br>Подсчитавши в уме, <br>Сколько пчелок всего здесь собралось?<br><br>карт<br><br>5. Задача армянского ученого Анания Ширакаци (VII век н. э.).<br><br>"Один купец прошел через 3 города, и взыскивали с него в первом городе пошлины половину и треть имущества, и во втором городе половину и треть (с того, что осталось), и в третьем городе половину и треть (с того, что осталось). Когда он прибыл домой, у него осталось 11 денежков (денежных единиц). Итак, узнай, сколько всего денежков было вначале у купца?"<br><br>карт<br><br><br><br> | + | <br>[[Image:27.01-68.jpg|640px|Урок 20. Из истории дробей]]<br> <br> Потребность в более точных '''[[Урок 19. Измерения и дроби|измерениях величин]]''' привела к тому, что единицы измерения стали делить на несколько равных частей: 2, 4, 8 и т. д. Каждая часть первоначальной мерки получала свое собственное название. Например, половину в Древней Руси называли еш;е полтиной, о четвертой части говорили — ЧЕТЬ, о восьмой части — ПОЛЧЕТЬ, о шестнадцатой части —ПОЛПОЛЧЕТЬ и т. д. Равные части целой мерки называли долями: четвертые доли, восьмые, шестнадцатые и т. д.<br><br>[[Image:27.01-69.jpg|Задача]]<br><br>Интересная система дробей была в Древнем Риме. Она основывалась на делении древнеримской единицы массы, которая называлась АСС. Асе делили на 12 равных частей. Двенадцатую часть асса называли УНЦИЕЙ. Со временем унции стали применять для измерения других величин. Например, римлянин мог сказать, что он прошел 7 унций пути. При этом речь, конечно, не шла о взвешивании пути. Имелось в виду, что пройдено<br>семь "двенадцатых долей" пути.<br><br>[[Image:27.01-70.jpg|Задача]]<br> <br>Так постепенно происходил переход от конкретных дробей к отвлеченным дробям, не связанным с какой-нибудь определенной мерой.<br><br>[[Image:27.01-71.jpg|Задача]]<br><br>Запись дробей и алгоритмы действий с ними в древности были так сложны, что учение о дробях считалось самым трудным разделом арифметики. Чтобы его освоить, приходилось заучивать огромное число правил действий с дробями. Например, в Древнем Риме в ходу было всего 18 различных дробей: СЕМИС — половина асса, СЕКСТАНС — шестая его доля, СЕСКУНЦИЯ — восьмая, ТРИЕНС — треть асса, БЕС — две трети, СЕМИУНЦИЯ — пол-унции, или одна двадцать четвертая доля асса, и т. д. Чтобы работать с долями, надо было твердо знать, что при сложении ТРИЕНСА и СЕКСТАНСА получается СЕМИС, а при умножении БЕСА на СЕСКУНЦИЮ получается УНЦИЯ. Этих правил было так много, что умение оперировать дробями воспринималось как чудо. Поэтому всегда и везде знание дробей пользовалось особым почетом и уважением. Так, например, автор славянской рукописи XVI века пишет: "Несть се дивно, что в целых, а то похвально, что в долях ..." Об этом же писал в своей знаменитой "Арифметике" русский '''[http://xvatit.com/busines/jobs-career/ математик]''' XVIII века Л. Ф. Магницкий:<br><br>[[Image:27.01-72.jpg|Задача]] |
| | + | |
| | + | <br> Но несть тот арифметик. <br> Иже в целых ответчик, <br> А в долях ничтоже <br> Отвеш;ате возможе.<br><br> Тем же о ты радеяй. <br> Буди в частях умеяй.<br><br>В древности для основных дробей, которые были в обиходе, существовали индивидуальные знаки, а остальные '''[[Тема 52. Дроби|дроби]]''' получались из основных дробей с помощью арифметических действий. Вот как, например, обозначались некоторые '''[[Презентація уроку на тему "Дроби"|дроби]]''' в Древнем Египте:<br><br>[[Image:27.01-73.jpg|640px|Задача]] |
| | + | |
| | + | <br>У древних римлян унция обозначалась чертой "—", половина асса, или 6 унций, — S (первой в латинском слове semis — половина). Например, семь двенадцатых записывались так: "S—" |
| | + | |
| | + | Современная система записи дробей с числителем и знаменателем была создана в Индии, только там не писали дробной черты. А записывать '''[[Дробові числа. Звичайні дроби.|дробь]]''' в точности так, как сейчас, стали арабы. Общеупотребительной эта запись дробей стала лишь в XVI веке.<br><br>[[Image:27.01-74.jpg|Задача]]<br> <br>''' Старинные задачи с дробями '''<br><br>'''1. В произведении знаменитого римского поэта I века до н. э. Горация так описана беседа учителя с учеником в одной из римских школ этой эпохи:''' |
| | + | |
| | + | '''Учитель'''. Пусть скажет сын Альбина, сколько останется, если от пяти унций отнять одну унцию? |
| | + | |
| | + | '''Ученик.''' Одна треть. |
| | + | |
| | + | '''Учитель.''' Правильно. Ты сумеешь беречь свое имугцество. |
| | + | |
| | + | Пользуясь схемой, докажи, что ученик был прав:<br> <br>[[Image:27.01-75.jpg|640px|Задача]]<br><br>'''2. Задача из "Арифметики" известного среднеазиатского математи-ка Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.).''' |
| | + | |
| | + | "Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10".<br><br>[[Image:27.01-76.jpg|640px|Задача]]<br> <br>'''3. Задача из "Папируса Ахмеса" (Египет, 1850 г. до н. э.), "Приходит пастух с 70 быками. Его спрашивают:''' |
| | + | |
| | + | — Сколько приводишь ты своего многочисленного стада? |
| | + | |
| | + | Пастух отвечает: |
| | + | |
| | + | — Я привожу две трети от трети скота. Сочти!" |
| | + | |
| | + | Используя схему, найди, сколько быков было во всем стаде?<br> <br>[[Image:27.01-77.jpg|640px|Задача]]<br> <br>'''4. Староиндийская задача математика Сриддхары (XI век н. э.).'''<br> <br>Есть кадамба цветок. <br>На один лепесток <br>Пчелок пятая часть опустилась.<br><br> Рядом тут же росла <br> Вся в цвету сименгда, <br> И на ней третья часть поместилась.<br><br>Разность их ты найди, <br>Ее трижды сложи <br>И тех пчел на кутай посади.<br><br> Только две не нашли <br> Себе место нигде.<br> Все летали то взад, то вперед и везде <br> Ароматом цветов наслаждались.<br><br>Назови теперь мне. <br>Подсчитавши в уме, <br>Сколько пчелок всего здесь собралось?<br><br>[[Image:27.01-78.jpg|640px|Задача]]<br>'''<br>5. Задача армянского ученого Анания Ширакаци (VII век н. э.).'''<br><br>"Один купец прошел через 3 города, и взыскивали с него в первом городе пошлины половину и треть имущества, и во втором городе половину и треть (с того, что осталось), и в третьем городе половину и треть (с того, что осталось). Когда он прибыл домой, у него осталось 11 денежков (денежных единиц). Итак, узнай, сколько всего денежков было вначале у купца?"<br><br>[[Image:27.01-79.jpg|640px|Задача]] |
| | + | |
| | + | |
| | + | |
| | + | <br><br><br><br> |
| | | | |
| | <br> ''Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. - М.: Издательство "Ювента", 2005, - 64 с.: ил.'' | | <br> ''Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. - М.: Издательство "Ювента", 2005, - 64 с.: ил.'' |
Текущая версия на 13:53, 20 июля 2012
Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 20. Из истории дробей

Потребность в более точных измерениях величин привела к тому, что единицы измерения стали делить на несколько равных частей: 2, 4, 8 и т. д. Каждая часть первоначальной мерки получала свое собственное название. Например, половину в Древней Руси называли еш;е полтиной, о четвертой части говорили — ЧЕТЬ, о восьмой части — ПОЛЧЕТЬ, о шестнадцатой части —ПОЛПОЛЧЕТЬ и т. д. Равные части целой мерки называли долями: четвертые доли, восьмые, шестнадцатые и т. д.

Интересная система дробей была в Древнем Риме. Она основывалась на делении древнеримской единицы массы, которая называлась АСС. Асе делили на 12 равных частей. Двенадцатую часть асса называли УНЦИЕЙ. Со временем унции стали применять для измерения других величин. Например, римлянин мог сказать, что он прошел 7 унций пути. При этом речь, конечно, не шла о взвешивании пути. Имелось в виду, что пройдено
семь "двенадцатых долей" пути.
Так постепенно происходил переход от конкретных дробей к отвлеченным дробям, не связанным с какой-нибудь определенной мерой.

Запись дробей и алгоритмы действий с ними в древности были так сложны, что учение о дробях считалось самым трудным разделом арифметики. Чтобы его освоить, приходилось заучивать огромное число правил действий с дробями. Например, в Древнем Риме в ходу было всего 18 различных дробей: СЕМИС — половина асса, СЕКСТАНС — шестая его доля, СЕСКУНЦИЯ — восьмая, ТРИЕНС — треть асса, БЕС — две трети, СЕМИУНЦИЯ — пол-унции, или одна двадцать четвертая доля асса, и т. д. Чтобы работать с долями, надо было твердо знать, что при сложении ТРИЕНСА и СЕКСТАНСА получается СЕМИС, а при умножении БЕСА на СЕСКУНЦИЮ получается УНЦИЯ. Этих правил было так много, что умение оперировать дробями воспринималось как чудо. Поэтому всегда и везде знание дробей пользовалось особым почетом и уважением. Так, например, автор славянской рукописи XVI века пишет: "Несть се дивно, что в целых, а то похвально, что в долях ..." Об этом же писал в своей знаменитой "Арифметике" русский математик XVIII века Л. Ф. Магницкий:
Но несть тот арифметик.
Иже в целых ответчик,
А в долях ничтоже
Отвеш;ате возможе.
Тем же о ты радеяй.
Буди в частях умеяй.
В древности для основных дробей, которые были в обиходе, существовали индивидуальные знаки, а остальные дроби получались из основных дробей с помощью арифметических действий. Вот как, например, обозначались некоторые дроби в Древнем Египте:

У древних римлян унция обозначалась чертой "—", половина асса, или 6 унций, — S (первой в латинском слове semis — половина). Например, семь двенадцатых записывались так: "S—"
Современная система записи дробей с числителем и знаменателем была создана в Индии, только там не писали дробной черты. А записывать дробь в точности так, как сейчас, стали арабы. Общеупотребительной эта запись дробей стала лишь в XVI веке.
Старинные задачи с дробями
1. В произведении знаменитого римского поэта I века до н. э. Горация так описана беседа учителя с учеником в одной из римских школ этой эпохи:
Учитель. Пусть скажет сын Альбина, сколько останется, если от пяти унций отнять одну унцию?
Ученик. Одна треть.
Учитель. Правильно. Ты сумеешь беречь свое имугцество.
Пользуясь схемой, докажи, что ученик был прав:
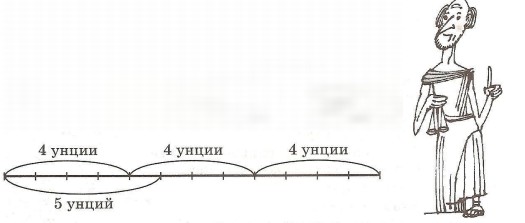
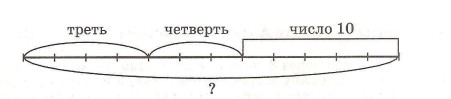
2. Задача из "Арифметики" известного среднеазиатского математи-ка Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.).
"Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10".
3. Задача из "Папируса Ахмеса" (Египет, 1850 г. до н. э.), "Приходит пастух с 70 быками. Его спрашивают:
— Сколько приводишь ты своего многочисленного стада?
Пастух отвечает:
— Я привожу две трети от трети скота. Сочти!"
Используя схему, найди, сколько быков было во всем стаде?

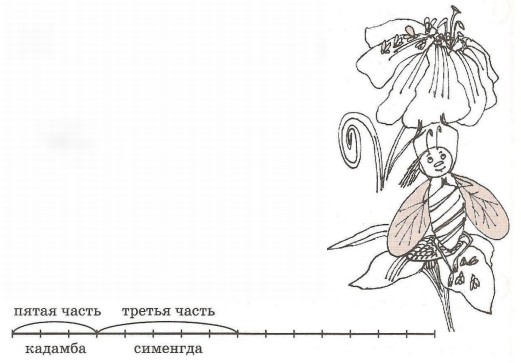
4. Староиндийская задача математика Сриддхары (XI век н. э.).
Есть кадамба цветок.
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда,
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на кутай посади.
Только две не нашли
Себе место нигде.
Все летали то взад, то вперед и везде
Ароматом цветов наслаждались.
Назови теперь мне.
Подсчитавши в уме,
Сколько пчелок всего здесь собралось?
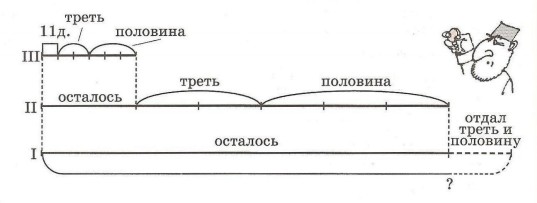
5. Задача армянского ученого Анания Ширакаци (VII век н. э.).
"Один купец прошел через 3 города, и взыскивали с него в первом городе пошлины половину и треть имущества, и во втором городе половину и треть (с того, что осталось), и в третьем городе половину и треть (с того, что осталось). Когда он прибыл домой, у него осталось 11 денежков (денежных единиц). Итак, узнай, сколько всего денежков было вначале у купца?"
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. - М.: Издательство "Ювента", 2005, - 64 с.: ил.
Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 4 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|






















