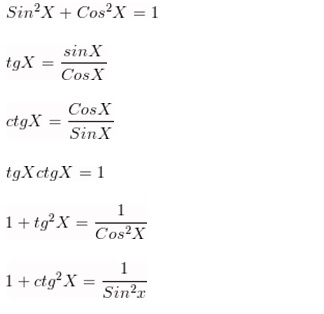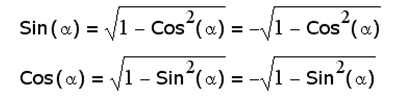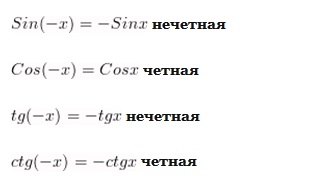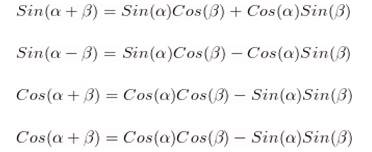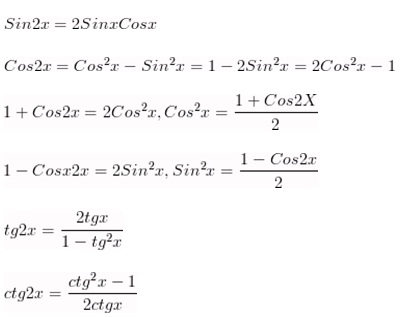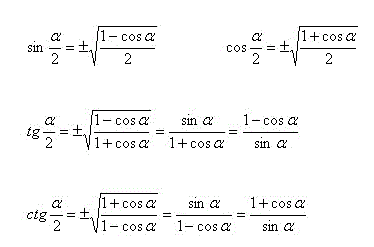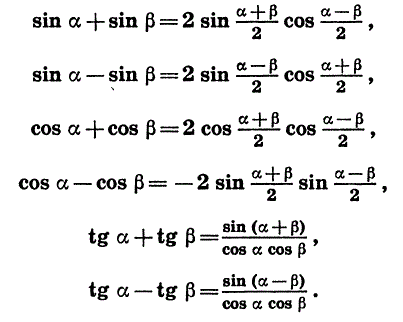|
|
| (2 промежуточные версии не показаны) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, шпаргалки, урок, Тригонометрические функции, Основные результаты </metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 10 класс, шпаргалки, урок, Тригонометрические функции, Основные результаты </metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Тригонометрические функции. Основные результаты''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>>Математика: Тригонометрические функции. Основные результаты''' |
| | | | |
| | Шпаргалки к теме '''«[[Тригонометрические функции. Основные результаты|Тригонометрические функции. Основные результаты]]»'''. | | Шпаргалки к теме '''«[[Тригонометрические функции. Основные результаты|Тригонометрические функции. Основные результаты]]»'''. |
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
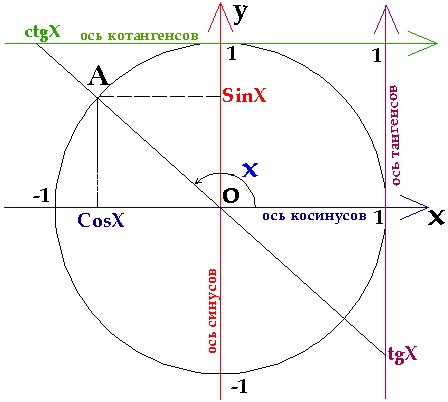
| - | '''Определение тригонометрических функций:''' | + | '''Определение тригонометрических функций:''' |
| | | | |
| - | <br>[[Image:Img 16.08.2012 01.jpg|Определение тригонометрических функций]]<br> | + | <br>[[Image:Img 16.08.2012 01.jpg|320px|Определение тригонометрических функций]]<br> |
| | | | |
| | <br>'''Определение:''' '''синусом''' угла поворота на называется ордината точки, изображающей данный угол. | | <br>'''Определение:''' '''синусом''' угла поворота на называется ордината точки, изображающей данный угол. |
| | | | |
| - | '''Определение: косинусом''' угла поворота называется абсцисса точки, изображающей данный угол. | + | '''Определение: косинусом''' угла поворота называется абсцисса точки, изображающей данный угол. |
| | | | |
| - | '''Определение:''' '''тангенсом''' угла поворота называется отношение ординаты точки, изображающей угол, >к ее абсциссе. | + | '''Определение:''' '''тангенсом''' угла поворота называется отношение ординаты точки, изображающей угол, >к ее абсциссе. |
| | | | |
| | '''Определение: котангенсом''' угла поворота называется отношение абсциссы точки, изображающей данный угол к ее ординате. | | '''Определение: котангенсом''' угла поворота называется отношение абсциссы точки, изображающей данный угол к ее ординате. |
| | | | |
| - | '''Основные тригонометрические свойства:''' | + | '''Основные тригонометрические свойства:''' |
| | | | |
| - | <br>[[Image:Img 16.08.2012 02.jpg|Основные тригонометрические свойства]]<br> | + | <br>[[Image:Img 16.08.2012 02.jpg|320px|Основные тригонометрические свойства]]<br> |
| | | | |
| - | [[Image:Img 16.08.2012 02-1.jpg|Основные тригонометрические свойства]]<br> | + | [[Image:Img 16.08.2012 02-1.jpg|320px|Основные тригонометрические свойства]]<br> |
| | | | |
| - | '''<br>Четность и нечетность тригонометрических функций:''' | + | '''<br>Четность и нечетность тригонометрических функций:''' |
| | | | |
| | <br>[[Image:Img 16.08.2012 03.jpg|Четность и нечетность тригонометрических функций]]<br> | | <br>[[Image:Img 16.08.2012 03.jpg|Четность и нечетность тригонометрических функций]]<br> |
| Строка 33: |
Строка 33: |
| | Функция называется'''четной''', если противоположным значениям аргумента соответствуют равные значения функции. | | Функция называется'''четной''', если противоположным значениям аргумента соответствуют равные значения функции. |
| | | | |
| | + | <br> |
| | | | |
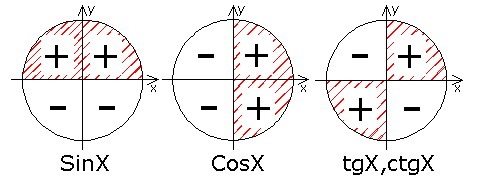
| | + | '''Знаки тригонометрических функций:''' |
| | | | |
| - | '''Знаки тригонометрических функций:'''
| + | [[Image:Img 16.08.2012 04.jpg|320px|Знаки тригонометрических функций]]<br> |
| - | | + | |
| - | [[Image:Img 16.08.2012 04.jpg|Знаки тригонометрических функций]]<br> | + | |
| | | | |
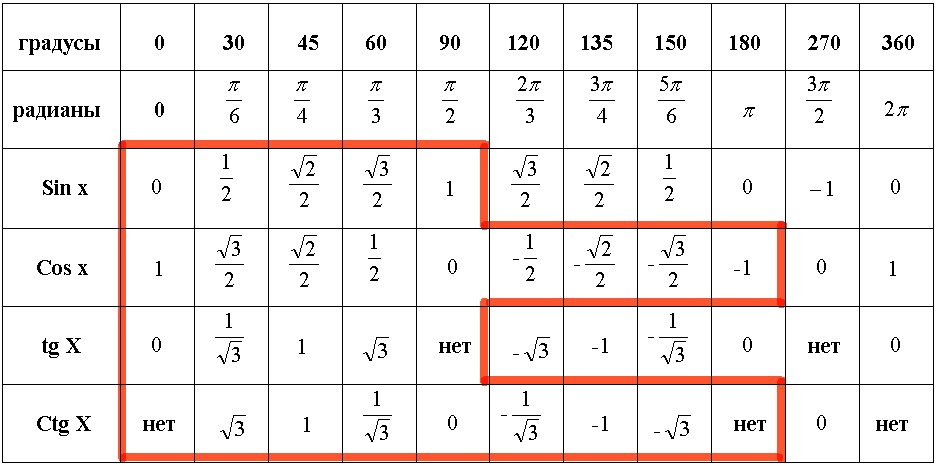
| - | '''<br>Таблица значений тригонометрических функций :''' | + | '''<br>Таблица значений тригонометрических функций :''' |
| | | | |
| - | [[Image:Img 16.08.2012 05.jpg|Таблица значений тригонометрических функций]]<br> | + | [[Image:Img 16.08.2012 05.jpg|550px|Таблица значений тригонометрических функций]]<br> |
| | | | |
| - | <br>'''Формулы сложения углов:''' | + | <br>'''Формулы сложения углов:''' |
| | | | |
| | [[Image:Img 16.08.2012 06.jpg|Формулы сложения углов]]<br> | | [[Image:Img 16.08.2012 06.jpg|Формулы сложения углов]]<br> |
| | | | |
| - | '''<br>Формулы двойного угла:''' | + | '''<br>Формулы двойного угла:''' |
| | | | |
| - | [[Image:Img 16.08.2012 07.jpg|Формулы двойного угла]]<br> | + | [[Image:Img 16.08.2012 07.jpg|370px|Формулы двойного угла]]<br> |
| | | | |
| - | '''<br>Формулы половинного угла:''' | + | '''<br>Формулы половинного угла:''' |
| | | | |
| | [[Image:Img 16.08.2012 08.gif|Формулы половинного угла]]<br> | | [[Image:Img 16.08.2012 08.gif|Формулы половинного угла]]<br> |
| | | | |
| - | '''<br>Формулы сложения тригонометрических функций:''' | + | '''<br>Формулы сложения тригонометрических функций:''' |
| | | | |
| | [[Image:Img 16.08.2012 09.gif|Таблица значений тригонометрических функций]]<br> | | [[Image:Img 16.08.2012 09.gif|Таблица значений тригонометрических функций]]<br> |
| | | | |
| | [[Category:Тригонометрические_функции._Основные_результаты._Шпаргалки]] | | [[Category:Тригонометрические_функции._Основные_результаты._Шпаргалки]] |