Сопряжения — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Сопряжения

 		Версия 21:06, 22 декабря 2010 (просмотреть исходный код)
User12  (Обсуждение | вклад)
← Предыдущая правка
		Текущая версия на 13:27, 27 августа 2012 (просмотреть исходный код)
ВикторияМора  (Обсуждение | вклад) 
 
		
(2 промежуточные версии не показаны)
Строка 3:
Строка 3:
 <metakeywords>Сопряжения</metakeywords><br>    <metakeywords>Сопряжения</metakeywords><br>  
  
- &nbsp;&nbsp;&nbsp;   + Плавный переход одной линии в другую называется '''сопряжением'''. Общая для сопрягаемых линий точка называется точкой сопряжения, или точкой перехода. Для построения сопряжений надо найти центр сопряжения и точки сопряжений. Рассмотрим различные типы сопряжений. Сопряжение прямого угла.&nbsp;&nbsp;  
  
- &nbsp;&nbsp;&nbsp; Плавный переход одной линии в другую называется '''сопряжением'''. Общая для сопрягаемых линий точка называется точкой сопряжения, или точкой перехода. Для построения сопряжений надо найти центр сопряжения и точки сопряжений. Рассмотрим различные типы сопряжений.Сопряжение прямого угла.&nbsp;&nbsp; + <br>
  
- &nbsp;&nbsp; Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (Н=АВ). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные точки а и Ь являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и Ь проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70).   + Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (Н=АВ). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные [[Движение_точки_и_тела|точки]] а и Ь являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и Ь проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70).  
  
- &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер59.jpg|220x444px|Чер59.jpg]]<br>&nbsp;&nbsp; Сопряжение острого и тупого углов. Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу Н=АВ. Поочередно поставим ножку циркуля в две произвольные точки&nbsp;&nbsp; на каждой из сторон&nbsp; острого угла. Проведем четыре дуги внутри угла, как показано на рис. 71, а.<br>&nbsp;&nbsp; К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б). Из центра сопряжения опустим перпендикуляры на стороны угла. + [[Image:Чер59.jpg|170px|сопряжение прямого угла]]<br>
  
- &nbsp;&nbsp; Полученные точки а&nbsp; и&nbsp; Ь будут точками сопряжения (рис.71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (Н=АВ), проведем дугу сопряжения .   + Сопряжение острого и тупого углов. Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу Н=АВ. Поочередно поставим ножку циркуля в две произвольные точки на каждой из сторон&nbsp; острого угла. Проведем четыре дуги внутри угла, как показано на рис. 71, а.<br>
  
- &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер60.jpg|214x513px|Чер60.jpg]]<br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <br> + К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б). Из центра сопряжения опустим [[Задачі_до_теми_Теорема_про_три_перпендикуляри|перпендикуляр]]ы на стороны угла. 
  
- &nbsp;&nbsp;&nbsp; Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.Сопряжение двух параллельных прямых.Заданы две параллельные прямые и точка &lt;1, лежащая на одной из них (рис.72). Рассмотрим последовательность построения сопряжения двух прямых. В точке (1 восставим перпендикуляр до пересечения&nbsp; его с другой прямой. Точки d и е являются точками сопряжения. Разделив отрезок de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые.   + Полученные точки а&nbsp; и&nbsp; Ь будут точками сопряжения (рис.71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (Н=АВ), проведем дугу сопряжения.  
  
- &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер61.jpg|194x516px|Чер61.jpg]]<br>&nbsp;&nbsp;&nbsp; Сопряжение дуг двух окружностей дугой заданного радиуса.  
  
- &nbsp;&nbsp;&nbsp; Существует несколько типов сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и смешанное.Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы R<sub>1</sub> и R<sub></sub>2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом О<sub>1</sub>О = R<sub>1</sub> + R<sub></sub>, а другую O<sub>2O</sub> = R<sub>2</sub> + R. Точка пересечения вспомогательных дуг является центром сопряжения.   + [[Image:Чер60.jpg|170px|острый угол]]
  
- &nbsp;&nbsp; Точки сопряжения K лежат в пересечении прямых О<sub>1</sub>О и O<sub>2O</sub> с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей (рис. 73, б).  
  
- &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер62.jpg|331x451px]]<br>&nbsp;&nbsp;&nbsp; Внутреннее сопряжение дуг двух окружностей дугой заданного радиуса .При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис. 74). Даны две дуги окружностей с центром O<sub>1</sub> и O<sub>2</sub>, радиусы которых соответственно равны R<sub>1</sub> и R<sub>2</sub>. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим центр сопряжения. Для этого из центра O<sub>1</sub> радиусом, равным R—R<sub>1</sub> и из центра O<sub>2</sub> радиусом, равным R—R<sub>2</sub>, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ОО<sub>1</sub> и OO<sub>2</sub>, соединяющих центры дуг окружностей с центром сопряжения.<br>[[Image:чер63.jpg]]<br> + Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.Сопряжение двух параллельных прямых.Заданы две параллельные прямые и [[Лазеры_на_квантовых_точках|точка]] &lt;1, лежащая на одной из них (рис.72). Рассмотрим последовательность построения сопряжения двух прямых. В точке (1 восставим перпендикуляр до пересечения&nbsp; его с другой прямой. Точки d и е являются точками сопряжения. Разделив [[Отрезок._Полные_уроки|отрезок]] de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые. 
  
- &nbsp;&nbsp;&nbsp; Вывод. Определяя величину радиусов вспомога¬тельных дуг, следует:<br>а) при внешнем сопряжении брать сумму радиусов заданных дуг и радиуса сопряжения, т. е. R<sub>1</sub> + R; R<sub>2</sub> + R (рис. 73);<br>б) при внутреннем сопряжении нужно использовать разность радиуса сопряжения R и радиусов заданных дуг окружностей, т. е. R—R<sub>1</sub> и R—R<sub>2</sub> (рис. 74).<br>[[Image:чер64.jpg]] +  
  + [[Image:Чер61.jpg|170px|Сопряжение]]
  +  
  + '''Сопряжение дуг двух окружностей дугой заданного радиуса'''
  +  
  + Существует несколько типов сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и смешанное.Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы R<sub>1</sub> и R2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом О<sub>1</sub>О = R<sub>1</sub> + R, а другую O<sub>2O</sub> = R<sub>2</sub> + R. Точка пересечения вспомогательных дуг является центром сопряжения. 
  +  
  + Точки сопряжения K лежат в пересечении прямых О<sub>1</sub>О и O<sub>2O</sub> с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей (рис. 73, б). 
  +  
  + [[Image:Чер62.jpg|250px|Сопряжение]]<br>
  +  
  + Внутреннее сопряжение дуг двух окружностей дугой заданного радиуса .При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис. 74). Даны две дуги окружностей с центром O<sub>1</sub> и O<sub>2</sub>, радиусы которых соответственно равны R<sub>1</sub> и R<sub>2</sub>. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим [[Выделение_сюжетно-композиционного_центра|центр]] сопряжения. Для этого из центра O<sub>1</sub> радиусом, равным R—R<sub>1</sub> и из центра O<sub>2</sub> радиусом, равным R—R<sub>2</sub>, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ОО<sub>1</sub> и OO<sub>2</sub>, соединяющих центры дуг окружностей с центром сопряжения.
  +  
  + <br>
  + [[Image:Чер63.jpg|250px|центр]]<br> 
  +  
  +  
  + '''Вывод'''. Определяя величину радиусов вспомогательных дуг, следует:<br>а) при внешнем сопряжении брать сумму радиусов заданных дуг и радиуса сопряжения, т. е. R<sub>1</sub> + R; R<sub>2</sub> + R (рис. 73);<br>б) при внутреннем сопряжении нужно использовать разность радиуса сопряжения R и радиусов заданных дуг окружностей, т. е. R—R<sub>1</sub> и R—R<sub>2</sub> (рис. 74).<br>
  + [[Image:Чер64.jpg|250px|изображение и чертеж]]  
  +  
  +  
  + '''Вопросы и задания'''<br>''1. Что называется сопряжением?<br>2. Какая точка называется центром сопряжения?<br>3. Какие точки являются точками сопряжения?''<br> 
  +  
  +  
  + '''Графическая работа'''<br>По наглядному [[Изображения_на_сборочном_чертеже|изображению]] детали выполните ее чертеж, применяя правила построения сопряжений (рис. 75).<br><br>''Н.А.Гордеенко, В.В.Степакова - Черчение.,[[9_класс_уроки|9 класс]]<br>Отослано читателями из интернет-сайтов''<br> 
  
  
Строка 43:
Строка 65:
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы    [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников    [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
-   +  
   '''<u>Иллюстрации</u>'''    '''<u>Иллюстрации</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''    '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
Строка 65:
Строка 87:
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке      [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке  
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми      [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми  
-   +  
   '''<u>Только для учителей</u>'''    '''<u>Только для учителей</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''    '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
Строка 74:
Строка 96:
         
         
-   '''<u>Интегрированные уроки</u>'''<u> +  '''<u>Интегрированные уроки</u>'''<u>
   </u>    </u>
  
Текущая версия на 13:27, 27 августа 2012
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Сопряжения  

 
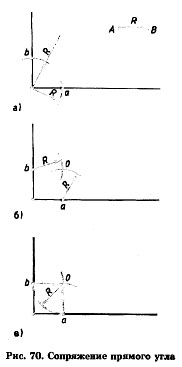
Плавный переход одной линии в другую называется сопряжением. Общая для сопрягаемых линий точка называется точкой сопряжения, или точкой перехода. Для построения сопряжений надо найти центр сопряжения и точки сопряжений. Рассмотрим различные типы сопряжений. Сопряжение прямого угла.   


Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (Н=АВ). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные точки а и Ь являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и Ь проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70). 


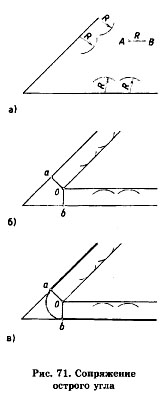
Сопряжение острого и тупого углов. Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу Н=АВ. Поочередно поставим ножку циркуля в две произвольные точки на каждой из сторон  острого угла. Проведем четыре дуги внутри угла, как показано на рис. 71, а.

К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б). Из центра сопряжения опустим перпендикуляры на стороны угла. 
Полученные точки а  и  Ь будут точками сопряжения (рис.71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (Н=АВ), проведем дугу сопряжения. 





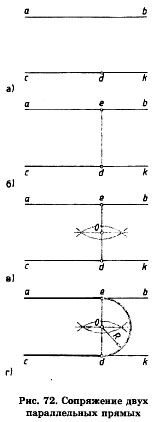
Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.Сопряжение двух параллельных прямых.Заданы две параллельные прямые и точка <1, лежащая на одной из них (рис.72). Рассмотрим последовательность построения сопряжения двух прямых. В точке (1 восставим перпендикуляр до пересечения  его с другой прямой. Точки d и е являются точками сопряжения. Разделив отрезок de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые. 



Сопряжение дуг двух окружностей дугой заданного радиуса
Существует несколько типов сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и смешанное.Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы R₁ и R2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом О₁О = R₁ + R, а другую O_2O = R₂ + R. Точка пересечения вспомогательных дуг является центром сопряжения. 
Точки сопряжения K лежат в пересечении прямых О₁О и O_2O с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей (рис. 73, б). 


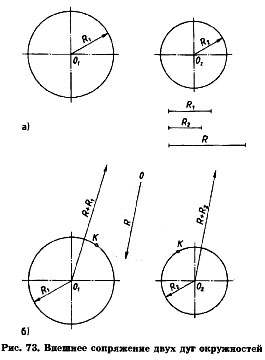
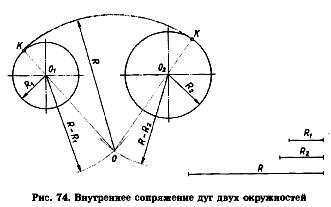
Внутреннее сопряжение дуг двух окружностей дугой заданного радиуса .При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис. 74). Даны две дуги окружностей с центром O₁ и O₂, радиусы которых соответственно равны R₁ и R₂. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим центр сопряжения. Для этого из центра O₁ радиусом, равным R—R₁ и из центра O₂ радиусом, равным R—R₂, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ОО₁ и OO₂, соединяющих центры дуг окружностей с центром сопряжения.




 


Вывод. Определяя величину радиусов вспомогательных дуг, следует:
а) при внешнем сопряжении брать сумму радиусов заданных дуг и радиуса сопряжения, т. е. R₁ + R; R₂ + R (рис. 73);
б) при внутреннем сопряжении нужно использовать разность радиуса сопряжения R и радиусов заданных дуг окружностей, т. е. R—R₁ и R—R₂ (рис. 74).

 


Вопросы и задания
1. Что называется сопряжением?
2. Какая точка называется центром сопряжения?
3. Какие точки являются точками сопряжения?
 


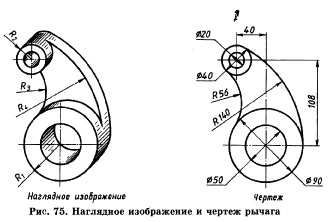
Графическая работа
По наглядному изображению детали выполните ее чертеж, применяя правила построения сопряжений (рис. 75).

Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс
Отослано читателями из интернет-сайтов
 



Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%A1%D0%BE%D0%BF%D1%80%D1%8F%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F»
@@ Строка 3: / Строка 3: @@
 <metakeywords>Сопряжения</metakeywords><br>
-&nbsp;&nbsp;&nbsp;
+Плавный переход одной линии в другую называется '''сопряжением'''. Общая для сопрягаемых линий точка называется точкой сопряжения, или точкой перехода. Для построения сопряжений надо найти центр сопряжения и точки сопряжений. Рассмотрим различные типы сопряжений. Сопряжение прямого угла.&nbsp;&nbsp;
-&nbsp;&nbsp;&nbsp; Плавный переход одной линии в другую называется '''сопряжением'''. Общая для сопрягаемых линий точка называется точкой сопряжения, или точкой перехода. Для построения сопряжений надо найти центр сопряжения и точки сопряжений. Рассмотрим различные типы сопряжений.Сопряжение прямого угла.&nbsp;&nbsp;
+<br>
-&nbsp;&nbsp; Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (Н=АВ). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные точки а и Ь являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и Ь проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70).
+Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (Н=АВ). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные [[Движение_точки_и_тела|точки]] а и Ь являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и Ь проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70).
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер59.jpg|220x444px|Чер59.jpg]]<br>&nbsp;&nbsp; Сопряжение острого и тупого углов. Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу Н=АВ. Поочередно поставим ножку циркуля в две произвольные точки&nbsp;&nbsp; на каждой из сторон&nbsp; острого угла. Проведем четыре дуги внутри угла, как показано на рис. 71, а.<br>&nbsp;&nbsp; К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б). Из центра сопряжения опустим перпендикуляры на стороны угла.
+[[Image:Чер59.jpg|170px|сопряжение прямого угла]]<br>
-&nbsp;&nbsp; Полученные точки а&nbsp; и&nbsp; Ь будут точками сопряжения (рис.71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (Н=АВ), проведем дугу сопряжения .
+Сопряжение острого и тупого углов. Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу Н=АВ. Поочередно поставим ножку циркуля в две произвольные точки на каждой из сторон&nbsp; острого угла. Проведем четыре дуги внутри угла, как показано на рис. 71, а.<br>
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер60.jpg|214x513px|Чер60.jpg]]<br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <br>
+К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б). Из центра сопряжения опустим [[Задачі_до_теми_Теорема_про_три_перпендикуляри|перпендикуляр]]ы на стороны угла.
-&nbsp;&nbsp;&nbsp; Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.Сопряжение двух параллельных прямых.Заданы две параллельные прямые и точка &lt;1, лежащая на одной из них (рис.72). Рассмотрим последовательность построения сопряжения двух прямых. В точке (1 восставим перпендикуляр до пересечения&nbsp; его с другой прямой. Точки d и е являются точками сопряжения. Разделив отрезок de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые.
+Полученные точки а&nbsp; и&nbsp; Ь будут точками сопряжения (рис.71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (Н=АВ), проведем дугу сопряжения.
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер61.jpg|194x516px|Чер61.jpg]]<br>&nbsp;&nbsp;&nbsp; Сопряжение дуг двух окружностей дугой заданного радиуса.
-&nbsp;&nbsp;&nbsp; Существует несколько типов сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и смешанное.Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы R<sub>1</sub> и R<sub></sub>2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом О<sub>1</sub>О = R<sub>1</sub> + R<sub></sub>, а другую O<sub>2O</sub> = R<sub>2</sub> + R. Точка пересечения вспомогательных дуг является центром сопряжения.
+[[Image:Чер60.jpg|170px|острый угол]]
-&nbsp;&nbsp; Точки сопряжения K лежат в пересечении прямых О<sub>1</sub>О и O<sub>2O</sub> с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей (рис. 73, б).
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер62.jpg|331x451px]]<br>&nbsp;&nbsp;&nbsp; Внутреннее сопряжение дуг двух окружностей дугой заданного радиуса .При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис. 74). Даны две дуги окружностей с центром O<sub>1</sub> и O<sub>2</sub>, радиусы которых соответственно равны R<sub>1</sub> и R<sub>2</sub>. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим центр сопряжения. Для этого из центра O<sub>1</sub> радиусом, равным R—R<sub>1</sub> и из центра O<sub>2</sub> радиусом, равным R—R<sub>2</sub>, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ОО<sub>1</sub> и OO<sub>2</sub>, соединяющих центры дуг окружностей с центром сопряжения.<br>[[Image:чер63.jpg]]<br>
+Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.Сопряжение двух параллельных прямых.Заданы две параллельные прямые и [[Лазеры_на_квантовых_точках|точка]] &lt;1, лежащая на одной из них (рис.72). Рассмотрим последовательность построения сопряжения двух прямых. В точке (1 восставим перпендикуляр до пересечения&nbsp; его с другой прямой. Точки d и е являются точками сопряжения. Разделив [[Отрезок._Полные_уроки|отрезок]] de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые.
-&nbsp;&nbsp;&nbsp; Вывод. Определяя величину радиусов вспомога¬тельных дуг, следует:<br>а) при внешнем сопряжении брать сумму радиусов заданных дуг и радиуса сопряжения, т. е. R<sub>1</sub> + R; R<sub>2</sub> + R (рис. 73);<br>б) при внутреннем сопряжении нужно использовать разность радиуса сопряжения R и радиусов заданных дуг окружностей, т. е. R—R<sub>1</sub> и R—R<sub>2</sub> (рис. 74).<br>[[Image:чер64.jpg]]
+[[Image:Чер61.jpg|170px|Сопряжение]]
+'''Сопряжение дуг двух окружностей дугой заданного радиуса'''
+Существует несколько типов сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и смешанное.Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы R<sub>1</sub> и R2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом О<sub>1</sub>О = R<sub>1</sub> + R, а другую O<sub>2O</sub> = R<sub>2</sub> + R. Точка пересечения вспомогательных дуг является центром сопряжения.
+Точки сопряжения K лежат в пересечении прямых О<sub>1</sub>О и O<sub>2O</sub> с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей (рис. 73, б).
+[[Image:Чер62.jpg|250px|Сопряжение]]<br>
+Внутреннее сопряжение дуг двух окружностей дугой заданного радиуса .При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис. 74). Даны две дуги окружностей с центром O<sub>1</sub> и O<sub>2</sub>, радиусы которых соответственно равны R<sub>1</sub> и R<sub>2</sub>. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим [[Выделение_сюжетно-композиционного_центра|центр]] сопряжения. Для этого из центра O<sub>1</sub> радиусом, равным R—R<sub>1</sub> и из центра O<sub>2</sub> радиусом, равным R—R<sub>2</sub>, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ОО<sub>1</sub> и OO<sub>2</sub>, соединяющих центры дуг окружностей с центром сопряжения.
+<br>
+[[Image:Чер63.jpg|250px|центр]]<br>
+'''Вывод'''. Определяя величину радиусов вспомогательных дуг, следует:<br>а) при внешнем сопряжении брать сумму радиусов заданных дуг и радиуса сопряжения, т. е. R<sub>1</sub> + R; R<sub>2</sub> + R (рис. 73);<br>б) при внутреннем сопряжении нужно использовать разность радиуса сопряжения R и радиусов заданных дуг окружностей, т. е. R—R<sub>1</sub> и R—R<sub>2</sub> (рис. 74).<br>
+[[Image:Чер64.jpg|250px|изображение и чертеж]]
+'''Вопросы и задания'''<br>''1. Что называется сопряжением?<br>2. Какая точка называется центром сопряжения?<br>3. Какие точки являются точками сопряжения?''<br>
+'''Графическая работа'''<br>По наглядному [[Изображения_на_сборочном_чертеже|изображению]] детали выполните ее чертеж, применяя правила построения сопряжений (рис. 75).<br><br>''Н.А.Гордеенко, В.В.Степакова - Черчение.,[[9_класс_уроки|9 класс]]<br>Отослано читателями из интернет-сайтов''<br>
@@ Строка 43: / Строка 65: @@
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
   '''<u>Иллюстрации</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
@@ Строка 65: / Строка 87: @@
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
   '''<u>Только для учителей</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
@@ Строка 74: / Строка 96: @@
-  '''<u>Интегрированные уроки</u>'''<u>
+ '''<u>Интегрированные уроки</u>'''<u>
   </u>

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: