|
|
|
| (3 промежуточные версии не показаны) | | Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''Эллипс — плоская кривая, являющаяся геометрическим местом точек, сумма расстояний от каждой из которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.'''<br> Чтобы построить эллипс, нужно найти как можно больше точек, принадлежащих этой кривой (рис. 76). Построение эллипса начинаем с проведения взаимно перпендикулярных штрихпунктирных линий, пересечение которых дает точку О. Из нее строим две концентрические окружности (окружности, имеющие общий центр) диаметрами АВ и СО, величина которых выбирается произвольно (рис. 76, а).<br> Разделим большую окружность на произвольное количество частей, например, на 12 равных, как показано на рис. 76, а. Соединим точки деления с центром О, разделив таким образом окружность меньшего диаметра на такое же количество частей. Из точек, полученных при делении меньшей окружности (за исключением точек С и Б), проводим горизонтальные линии, параллельные АВ (рис. 76, а). Из точек деления, полученных на большей окружности (за исключением точек 1, 4, 7, 10), проводим вертикальные линии, параллельные СО, до пересечения их с ранее проведенными горизонтальными прямыми (рис. 76, б). Таким образом мы получили ряд точек, принадлежащих эллипсу. Эллипсу также принадлежат точки А, В, С, Б. Последовательно соединяя точки плавной кривой, получим изображение эллипса, которое обводится с помощью лекал (рис. 76, в).<br>
| + | '''Эллипс '''— плоская кривая, являющаяся геометрическим местом точек, сумма расстояний от каждой из которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.<br> |
| | + | |
| | + | Чтобы построить эллипс, нужно найти как можно больше точек, принадлежащих этой кривой (рис. 76). Построение эллипса начинаем с проведения взаимно [[Паралельні_та_перпендикулярні_прямі|перпендикуляр]]ных штрихпунктирных [[Типы_линий|линий]], пересечение которых дает точку О. Из нее строим две концентрические окружности (окружности, имеющие общий центр) диаметрами АВ и СО, величина которых выбирается произвольно (рис. 76, а).<br> |
| | + | |
| | + | Разделим большую окружность на произвольное количество частей, например, на 12 равных, как показано на рис. 76, а. Соединим точки деления с центром О, разделив таким образом окружность меньшего диаметра на такое же количество частей. Из точек, полученных при делении меньшей окружности (за исключением точек С и Б), проводим [[Линия_горизонта|горизонт]]альные линии, параллельные АВ (рис. 76, а). Из точек деления, полученных на большей окружности (за исключением точек 1, 4, 7, 10), проводим вертикальные линии, параллельные СО, до пересечения их с ранее проведенными горизонтальными прямыми (рис. 76, б). Таким образом мы получили ряд точек, принадлежащих эллипсу. Эллипсу также принадлежат точки А, В, С, Б. Последовательно соединяя точки плавной кривой, получим изображение эллипса, которое обводится с помощью лекал (рис. 76, в).<br> |
| | + | |
| | + | |
| | + | |
| | + | [[Image:Черчн.jpg|Построение эллипса]]<br> |
| | + | |
| | + | |
| | + | Кривые, которые строятся с помощью лекал называются лекальными кривыми.<br> |
| | + | |
| | + | У эллипса различают две оси: большую ось (АВ) и малую ось (СО).Фокусы эллипса располагаются на его большой оси (АВ) симметрично относительно точки О. Расстояние между фокусами F1 и F2, '''называется фокальным.'''<br> |
| | + | |
| | + | Чтобы определить месторасположение фокусов на большой реи эллипса, выполняют следующие построения:<br> |
| | + | |
| | + | *разделим отрезок ОА пополам, получим точку O<sub>1</sub> |
| | + | *построим окружность радиусом О<sub>1</sub>А с центром в точке О<sub>1</sub> |
| | + | *точку Е соединяем с точкой А (рис. 76, г) ; |
| | + | *отрезок ЕА по величине равен половине фокального расстояния построенного эллипса; |
| | + | *[[Материалы,_принадлежности,_чертежные_инструменты._Подготовка_их_к_работе.|циркулем]] из точки О отложим по обе стороны на оси АВ отрезок АЕ, получив таким образом точки F<sub>1</sub> и F<sub>2</sub>, которые являются фокусами эллипса. |
| | + | |
| | + | <br>'''Вопросы и задания'''<br>''1. Какие лекальные кривые вы знаете?<br>2. Какая кривая называется эллипсом?<br>3. Дайте определение понятиям «фокус эллипса» и «фокальное расстояние».<br>4. В рабочих тетрадях постройте эллипс, большая ось которого равна 48,8 мм, а малая его ось — 28 мм. Для построения используйте описание, приведенное на рис. 76.''<br><br>''Н.А.Гордеенко, В.В.Степакова - Черчение.,[[9_класс_уроки|9 класс]]<br>Отослано читателями из интернет-сайтов''<br> |
| | + | |
| | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| Строка 21: |
Строка 46: |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' | | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| Строка 43: |
Строка 68: |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' | | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| Строка 52: |
Строка 77: |
| | | | |
| | | | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | '''<u>Интегрированные уроки</u>'''<u> |
| | </u> | | </u> |
| | | | |
Текущая версия на 13:30, 27 августа 2012
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Построение эллипса
Эллипс — плоская кривая, являющаяся геометрическим местом точек, сумма расстояний от каждой из которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
Чтобы построить эллипс, нужно найти как можно больше точек, принадлежащих этой кривой (рис. 76). Построение эллипса начинаем с проведения взаимно перпендикулярных штрихпунктирных линий, пересечение которых дает точку О. Из нее строим две концентрические окружности (окружности, имеющие общий центр) диаметрами АВ и СО, величина которых выбирается произвольно (рис. 76, а).
Разделим большую окружность на произвольное количество частей, например, на 12 равных, как показано на рис. 76, а. Соединим точки деления с центром О, разделив таким образом окружность меньшего диаметра на такое же количество частей. Из точек, полученных при делении меньшей окружности (за исключением точек С и Б), проводим горизонтальные линии, параллельные АВ (рис. 76, а). Из точек деления, полученных на большей окружности (за исключением точек 1, 4, 7, 10), проводим вертикальные линии, параллельные СО, до пересечения их с ранее проведенными горизонтальными прямыми (рис. 76, б). Таким образом мы получили ряд точек, принадлежащих эллипсу. Эллипсу также принадлежат точки А, В, С, Б. Последовательно соединяя точки плавной кривой, получим изображение эллипса, которое обводится с помощью лекал (рис. 76, в).
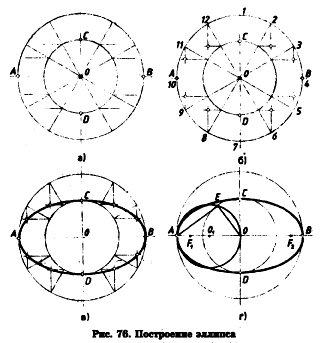
Кривые, которые строятся с помощью лекал называются лекальными кривыми.
У эллипса различают две оси: большую ось (АВ) и малую ось (СО).Фокусы эллипса располагаются на его большой оси (АВ) симметрично относительно точки О. Расстояние между фокусами F1 и F2, называется фокальным.
Чтобы определить месторасположение фокусов на большой реи эллипса, выполняют следующие построения:
- разделим отрезок ОА пополам, получим точку O1
- построим окружность радиусом О1А с центром в точке О1
- точку Е соединяем с точкой А (рис. 76, г) ;
- отрезок ЕА по величине равен половине фокального расстояния построенного эллипса;
- циркулем из точки О отложим по обе стороны на оси АВ отрезок АЕ, получив таким образом точки F1 и F2, которые являются фокусами эллипса.
Вопросы и задания
1. Какие лекальные кривые вы знаете?
2. Какая кривая называется эллипсом?
3. Дайте определение понятиям «фокус эллипса» и «фокальное расстояние».
4. В рабочих тетрадях постройте эллипс, большая ось которого равна 48,8 мм, а малая его ось — 28 мм. Для построения используйте описание, приведенное на рис. 76.
Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











