|
|
|
| (2 промежуточные версии не показаны) | | Строка 3: |
Строка 3: |
| | <metakeywords>Прямоугольные проекции отрезков прямых линий</metakeywords><br> | | <metakeywords>Прямоугольные проекции отрезков прямых линий</metakeywords><br> |
| | | | |
| - | Знание построения проекций точек дает нам возможность быстро освоить построение проекций отрезка прямой линии. Любой отрезок можно представить как определенную совокупность точек, поэтому, чтобы получить проекцию отрезка АВ на плоскости Н, нужно построить проекции точек А и В, затем соединить их между собой, получив тем самым проекцию отрезка прямой — аЬ (рис. 113).<br> Рассмотрим, как же проецируется отрезок на три взаимно перпендикулярные плоскости в зависимости от его расположения в пространстве.<br> '''Положение 1.''' Отрезок прямой наклонен ко всем трем плоскостям (рис. 114, а), поэтому на три плоскости проекций длина отрезка отображается с искажением (сокращением) размеров. Построение выполнено с помощью постоянной прямой чертежа (рис. 114, а).<br> '''Положение 2.''' Отрезок прямой перпендикулярен горизонтальной плоскости проекций.<br>
| + | Знание построения проекций точек дает нам возможность быстро освоить построение проекций отрезка прямой линии. Любой отрезок можно представить как определенную совокупность точек, поэтому, чтобы получить проекцию отрезка АВ на плоскости Н, нужно построить [[Проецирование|проекции точек]] А и В, затем соединить их между собой, получив тем самым проекцию отрезка прямой — аЬ (рис. 113).<br> |
| | | | |
| - | [[Image:черчн13.jpg]] | + | Рассмотрим, как же проецируется отрезок на три взаимно перпендикулярные плоскости в зависимости от его расположения в [[Изображение_пространственных_фигур_на_плоскости|пространстве]].<br> |
| | | | |
| - | [[Image:черчн14.jpg]]
| + | '''Положение 1.''' Отрезок прямой наклонен ко всем трем плоскостям (рис. 114, а), поэтому на три плоскости проекций длина отрезка отображается с искажением (сокращением) размеров. Построение выполнено с помощью постоянной прямой чертежа (рис. 114, а). |
| | | | |
| | + | '''Положение 2.''' Отрезок прямой перпендикулярен горизонтальной плоскости [[Аксонометрические_проекции|проекций]].<br> |
| | | | |
| | | | |
| - | В этом случае фронтальная и профильная проекции будут параллельны оси OZ, и отобразятся на плоскостях V и W в натуральную величину. На горизонтальной проекции отрезок прямой вырождается в точку (рис. 114, б).<br> '''Положение 3.''' Отрезок прямой перпендикулярен фронтальной плоскости проекций. В этом случае на плоскость V он спроецируется в виде точки. На горизонтальную (Н) и профильную (W) плоскости проекций он спроецируется в виде отрезков прямых, величины которых будут равны действительной величине проецируемого отрезка (рис. 114, в).<br> '''Положение 4. '''Отрезок прямой перпендикулярен профильной плоскости проекций. В этом случае он отобразится на нее точкой. На фронтальной и горизонтальной плоскостях проекций получим изображение отрезков прямых, величина которых равна натуральной величине отрезка (рис. 114, г).<br>'''Вывод:'''<br>1. Проекция отрезка прямой, полученная при прямоугольном проецировании на плоскость проекций, не может быть больше самого отрезка.<br>2. Если отрезок прямой параллелен плоскости проекций, то на нее он спроецируется в натуральную величину.<br>3. Если отрезок прямой перпендикулярен плоскости проекций, то на нее он спроецируется в точку.<br>4. Если в пространстве отрезок прямой наклонен к плоскости проекций, он проецируется на нее с искажением (т. е. размер проекции отрезка будет меньше действительного).<br>[[Image:черчн15.jpg]]
| |
| | | | |
| | + | [[Image:Черчн13.jpg|250px|Проекции]] |
| | + | |
| | + | [[Image:Черчн14.jpg|300px|Проекции]] |
| | + | |
| | + | <br> |
| | + | |
| | + | В этом случае фронтальная и профильная проекции будут параллельны оси OZ, и отобразятся на плоскостях V и W в натуральную величину. На горизонтальной проекции отрезок прямой вырождается в точку (рис. 114, б).<br> |
| | + | |
| | + | '''Положение 3.''' Отрезок прямой [[Перпендикуляр_и_наклонная._Полные_уроки|перпендикуляр]]ен фронтальной плоскости проекций. В этом случае на плоскость V он спроецируется в виде точки. На горизонтальную (Н) и профильную (W) плоскости проекций он спроецируется в виде отрезков прямых, величины которых будут равны действительной величине проецируемого отрезка (рис. 114, в).<br> |
| | + | |
| | + | '''Положение 4. '''Отрезок прямой перпендикулярен профильной плоскости проекций. В этом случае он отобразится на нее точкой. На фронтальной и горизонтальной плоскостях проекций получим [[Презентация_на_тему:_Как_кодируется_изображение?|изображение]] отрезков прямых, величина которых равна натуральной величине отрезка (рис. 114, г). |
| | + | |
| | + | <br>'''Вывод:'''<br>1. Проекция отрезка прямой, полученная при прямоугольном проецировании на плоскость проекций, не может быть больше самого отрезка.<br>2. Если отрезок прямой параллелен плоскости проекций, то на нее он спроецируется в натуральную величину.<br>3. Если отрезок прямой перпендикулярен плоскости проекций, то на нее он спроецируется в точку.<br>4. Если в пространстве [[Урок_1._Отрезок_и_его_части|отрезок]] прямой наклонен к плоскости проекций, он проецируется на нее с искажением (т. е. размер проекции отрезка будет меньше действительного). |
| | + | |
| | + | <br>[[Image:Черчн15.jpg|300px|отрезок прямой]] |
| | + | |
| | + | <br> |
| | + | |
| | + | '''Вопросы и задания'''<br>''1.Как надо расположить в пространстве отрезок прямой, чтобы на фронтальной плоскости проекций он спроецировался в точку?<br>2.Как вы понимаете выражение «[[Прямая_призма|прямая]] принадлежит плоскости»?<br>3.Всегда ли по величине проекции отрезка прямой можно определить его натуральную величину?<br>4.На наглядном изображении показано положение отрезка прямой в пространстве (рис. 115). Постройте чертеж данной прямой.<br>5.По двум проекциям отрезка найдите третью (рис. 116).''<br> |
| | + | |
| | + | <br> |
| | + | |
| | + | ''Н.А.Гордеенко, В.В.Степакова - Черчение.,[[9_класс_уроки|9 класс]]<br>Отослано читателями из интернет-сайтов'' |
| | | | |
| | | | |
| - | '''Вопросы и задания'''<br>1.Как надо расположить в пространстве отрезок прямой, чтобы на фронтальной плоскости проекций он спроецировался в точку?<br>2.Как вы понимаете выражение «прямая принадлежит плоскости»?<br>3.Всегда ли по величине проекции отрезка прямой можно определить его натуральную величину?<br>4.На наглядном изображении показано положение отрезка прямой в пространстве (рис. 115). Постройте чертеж данной прямой.<br>5.По двум проекциям отрезка найдите третью (рис. 116).<br>
| |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| Строка 31: |
Строка 53: |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' | | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| Строка 53: |
Строка 75: |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' | | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| Строка 62: |
Строка 84: |
| | | | |
| | | | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | '''<u>Интегрированные уроки</u>'''<u> |
| | </u> | | </u> |
| | | | |
Текущая версия на 14:16, 27 августа 2012
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Прямоугольные проекции отрезков прямых линий
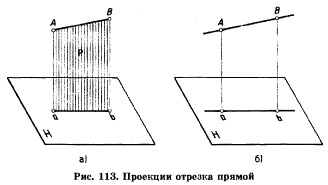
Знание построения проекций точек дает нам возможность быстро освоить построение проекций отрезка прямой линии. Любой отрезок можно представить как определенную совокупность точек, поэтому, чтобы получить проекцию отрезка АВ на плоскости Н, нужно построить проекции точек А и В, затем соединить их между собой, получив тем самым проекцию отрезка прямой — аЬ (рис. 113).
Рассмотрим, как же проецируется отрезок на три взаимно перпендикулярные плоскости в зависимости от его расположения в пространстве.
Положение 1. Отрезок прямой наклонен ко всем трем плоскостям (рис. 114, а), поэтому на три плоскости проекций длина отрезка отображается с искажением (сокращением) размеров. Построение выполнено с помощью постоянной прямой чертежа (рис. 114, а).
Положение 2. Отрезок прямой перпендикулярен горизонтальной плоскости проекций.
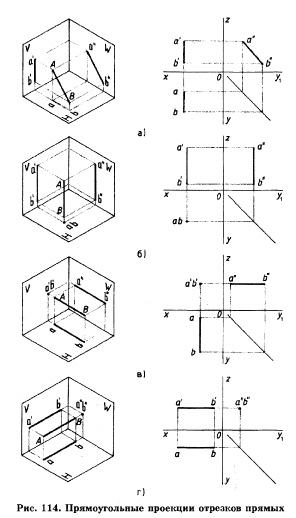
В этом случае фронтальная и профильная проекции будут параллельны оси OZ, и отобразятся на плоскостях V и W в натуральную величину. На горизонтальной проекции отрезок прямой вырождается в точку (рис. 114, б).
Положение 3. Отрезок прямой перпендикулярен фронтальной плоскости проекций. В этом случае на плоскость V он спроецируется в виде точки. На горизонтальную (Н) и профильную (W) плоскости проекций он спроецируется в виде отрезков прямых, величины которых будут равны действительной величине проецируемого отрезка (рис. 114, в).
Положение 4. Отрезок прямой перпендикулярен профильной плоскости проекций. В этом случае он отобразится на нее точкой. На фронтальной и горизонтальной плоскостях проекций получим изображение отрезков прямых, величина которых равна натуральной величине отрезка (рис. 114, г).
Вывод:
1. Проекция отрезка прямой, полученная при прямоугольном проецировании на плоскость проекций, не может быть больше самого отрезка.
2. Если отрезок прямой параллелен плоскости проекций, то на нее он спроецируется в натуральную величину.
3. Если отрезок прямой перпендикулярен плоскости проекций, то на нее он спроецируется в точку.
4. Если в пространстве отрезок прямой наклонен к плоскости проекций, он проецируется на нее с искажением (т. е. размер проекции отрезка будет меньше действительного).
Вопросы и задания
1.Как надо расположить в пространстве отрезок прямой, чтобы на фронтальной плоскости проекций он спроецировался в точку?
2.Как вы понимаете выражение «прямая принадлежит плоскости»?
3.Всегда ли по величине проекции отрезка прямой можно определить его натуральную величину?
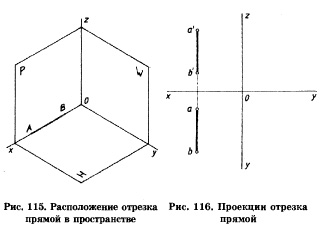
4.На наглядном изображении показано положение отрезка прямой в пространстве (рис. 115). Постройте чертеж данной прямой.
5.По двум проекциям отрезка найдите третью (рис. 116).
Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













