|
|
| (13 промежуточных версий не показаны.) |
| Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика]]>>[[Информатика 9 класс. Полные уроки]]>>Информатика: Двоичная система счисления.''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика]]>>[[Информатика 9 класс. Полные уроки]]>>Информатика: Двоичная система счисления.''' |
| | | | |
| - | Информатика, класс, урок, на тему, 9 класс, Двоичная система счисления. | + | <metakeywords>Информатика, класс, урок, на тему, 9 класс, Двоичная система счисления.</metakeywords><br> |
| | | | |
| - | Тема: Двоичная система счисления. | + | == Тема == |
| - | Цель: Рассказать об системах счисления. Дать представление о позиционной и непозиционной системах счисления. Изучить основы двоичной системы счиления.
| + | |
| - | [[Файл:desyti.jpg]]
| + | |
| - | В процессе эволюции человек использовал самые разные системы счисления, но наиболее удобной на практике оказалась именно десятичная система. Наверное, это было как-то связано с физиологией человеческого тела – у него человека на руках и ногах по десять пальцев.
| + | |
| - | {{#ev:youtube|8xyVYZz9zlY}}
| + | |
| - | Но не будем спешить - ведь не все же системы используют такое счисление.
| + | |
| - | Например, электронные вычислительные машины чрезвычайно эффективно используют двоичную систему счисления, в которой используются лишь две цифры - это 0 и 1.
| + | |
| - | [[Файл:i2i10.jpg]]
| + | |
| - | Причина проста – ведь с точки зрения техники машину с двумя состояниями проще создать, причем упрощаются различения этих состояний.
| + | |
| - | {{#ev:youtube|Tb50hr81zOI}}
| + | |
| - | Совокупность методов и приёмов для записи чисел цифровыми знаками называют системой счисления. Они разделяются на позиционные и непозиционные.
| + | |
| | | | |
| - | [[Файл:cxemasd.jpg]]
| + | *'''Двоичная система счисления ''' |
| - | В позиционной системе счисления используются число в определённом порядке для обозначения каких-либо чисел, а значение каждого символа зависит расположения этого символа по отношению к другим в том же числе. Пример - арабская десятичная система счисления.
| + | |
| | | | |
| - | В непозиционной системе все наоборот - значение каждого символа не зависит от его расположения по отношению к другим в том же числе. Пример – римские цифры.
| + | == Цель == |
| - | [[Файл:nepozicionnaya.jpg]]
| + | |
| | | | |
| - | {{#ev:youtube|vQ748FuizOM}}
| + | *Рассказать о системах счисления. |
| | + | *Дать представление о позиционной и непозиционной системах счисления. |
| | + | *Изучить основы двоичной системы счиcления. |
| | | | |
| - | Двоичная система счисления.
| + | == Ход урока == |
| | | | |
| - | И так, как уже было сказано, для компьютера самая подходящая система счисления – двоичная. В такой системе используются лишь два символа. И этот метод отлично «дружит» с техническими данными различных цифровых схем.
| + | === Системы счисления === |
| - | Оказалось, что представлять разные составляющие информации двумя состояниями очень удобно:
| + | |
| - | Тело намагничено или размагничено (дискеты, жесткие диски магнитные ленты);
| + | |
| - | Отверстие есть или нет (перфокарта)
| + | |
| - | Уровень сигнала большой или маленький.
| + | |
| - | {{#ev:youtube|2bPRHv-Foso}}
| + | |
| - | Для отображения таких состояний в цифровых системах нужно иметь электросхемы, принимающие два состояния и четко различающие значения электрической величины - потенциала или тока. Каждому из таких значений соответствует или 0 или 1 (обычно «0» представляет низкий уровень потенциала, а «1» – высокий.
| + | |
| - | Простота создания электросхем с двумя электрическими состояниями и есть причиной того, что двоичное представление чисел «лидирует» в мире современной цифровой техники.
| + | |
| | | | |
| | + | В процессе эволюции человек использовал самые разные '''[[История чисел и систем счисления. Полные уроки|системы счисления]]''' (восьмеричная, шестнадцатеричная и т.д), но наиболее удобной на практике оказалась именно '''[[Десятичная система счисления|десятичная система]]'''. |
| | | | |
| - | Также существуют термины, широко используемые в вычислительной сфере - бит, байт, слово.
| + | <br> |
| | | | |
| - | [[Файл:slovobit.jpg]] | + | [[Image:Desyti.jpg|480px|Десятичная система счисления]] <br> |
| | | | |
| - | Бит – это один двоичный разряд. Крайний слева бит числа - старший разряд (наибольший вес), крайний справа – младший (наименьший вес).
| + | <br> |
| - | Восьмибитовая единица есть байт.
| + | |
| - | Современные компьютеры перерабатывают информацию порциями (словами) по 8, 16 или 32 бита (1, 2 и 4 байта) и т.д.
| + | |
| | | | |
| | + | Наверное, это было как-то связано с '''[[Органи,фізіологічні й функціональні системи. Повні уроки|физиологией человеческого тела]]''' – у него человека на руках и ногах по десять пальцев. |
| | | | |
| - | Перевод чисел из одной системы счисления в другую.
| |
| - | {{#ev:youtube|anpbBxalAbM}}
| |
| | | | |
| - | При переводе чисел, например, из десятичной системы в двоичную, используется метод деления в столбик.
| |
| - | Попробуем проделать такую операцию с числом 567.
| |
| - | [[Файл:sxodii.jpg]]
| |
| | | | |
| - | При деление 567 на 2 выходит целое 283 и остаток 1.
| + | {{#ev:youtube|8xyVYZz9zlY}} |
| - | Проведем то же действие с числом 283 - целое 141, остаток 1.
| + | |
| - | Снова делим полученное целое число на 2 - и так до тех пор, пока целое число не станет меньше делителя.
| + | |
| - | А для того, чтобы получить число в двоичной системе счисления, нужно записать последнее целое число (в нашем случае это 1) и приписать к нему все полученные в во время деления остатки в обратном порядке.
| + | |
| | | | |
| | | | |
| - | Вопросы:
| |
| - | 1. Что такое система счисления?
| |
| - | 2. Позиционные и непозиционные системы счисления.
| |
| - | 3. Что представляет собой двоичная система счисления?
| |
| - | 4. Каким можно перевести число из десятичной системы в двоичную?
| |
| | | | |
| | + | Но не будем спешить - ведь не все же системы используют такое счисление. |
| | | | |
| | + | Например, '''[http://xvatit.com/it/fishki-ot-itshki/ электронные вычислительные машины]''' чрезвычайно эффективно используют '''[[Двоичная система счисления|двоичную систему счисления]]''', в которой используются лишь две цифры - это 0 и 1. |
| | | | |
| - | Список использованных источников:
| + | <br> |
| - | 1. Урок на тему: «Системы счисления», Дроводинова Л. В., г. Днепропетровск.
| + | |
| - | 2. Острейковский В.А., Полякова И.В. Информатика. Теория и практика. - Оникс, 2008 г.
| + | |
| - | 3. Андреева Е., Фалина И. Системы счисления и компьютерная арифметика. - Учебное пособие.- БИНОМ, 2004 г.
| + | |
| - | 4. Попов И.И., Партыка Т.Л. Вычислительная техника. – Форум, 2007 г.
| + | |
| | | | |
| | + | [[Image:I2i10.jpg|480px|Системы счисления]] |
| | | | |
| - | Отредактировано и выслано преподавателем Киевского национального университета им. Тараса Шевченка Соловьевым М. С.
| + | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | Причина проста – ведь с точки зрения техники машину с двумя состояниями проще создать, причем упрощаются различения этих состояний. |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | |
| | + | |
| | + | {{#ev:youtube|Tb50hr81zOI}} |
| | + | |
| | + | |
| | + | |
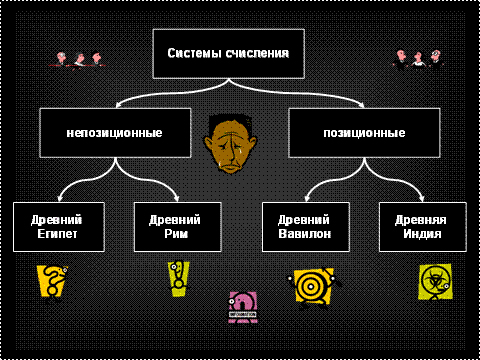
| | + | Совокупность методов и приёмов для записи чисел цифровыми знаками называют'''системой счисления. ''' |
| | + | |
| | + | Они разделяются на '''позиционные и непозиционные.''' |
| | + | |
| | + | <br> [[Image:Cxemasd.jpg|480px|Системы счисления]] |
| | + | |
| | + | <br> |
| | + | |
| | + | В '''[[Другие позиционные системы счисления|позиционной системе счисления]]''' используются число в определённом порядке для обозначения каких-либо чисел, а значение каждого символа зависит расположения этого символа по отношению к другим в том же числе. Пример - арабская десятичная система счисления. |
| | + | |
| | + | В '''непозиционной системе''' все наоборот - значение каждого символа не зависит от его расположения по отношению к другим в том же числе. |
| | + | |
| | + | Пример – римские цифры. |
| | + | |
| | + | |
| | + | |
| | + | [[Image:Nepozicionnaya.jpg|480px|Системы счисления]] |
| | + | |
| | + | <br> |
| | + | |
| | + | {{#ev:youtube|vQ748FuizOM}} |
| | + | |
| | + | === Двоичная система счисления === |
| | + | |
| | + | И так, как уже было сказано, для компьютера самая подходящая система счисления – двоичная. В такой системе используются лишь два символа - 0 и 1. |
| | + | |
| | + | И этот метод отлично «дружит» с техническими данными различных цифровых схем. Оказалось, что представлять разные составляющие информации двумя состояниями очень удобно: |
| | + | |
| | + | *Тело намагничено или размагничено (дискеты, жесткие диски магнитные ленты) |
| | + | *Отверстие есть или нет (перфокарта) |
| | + | *Уровень сигнала большой или маленький |
| | + | *Черный цвет или белый |
| | + | |
| | + | <br> |
| | + | |
| | + | {{#ev:youtube|2bPRHv-Foso}} |
| | + | |
| | + | <br> |
| | + | |
| | + | Для отображения таких состояний в цифровых системах нужно иметь электросхемы, принимающие два состояния и четко различающие значения электрической величины - '''потенциала или тока.''' Каждому из таких значений соответствует или 0 или 1 (обычно «0» представляет низкий уровень потенциала, а «1» – высокий). |
| | + | |
| | + | Простота создания электросхем с двумя электрическими состояниями и есть причиной того, что двоичное представление чисел «лидирует» в мире '''[http://xvatit.com/it/comp_primochki/ современной цифровой техники]'''. |
| | + | |
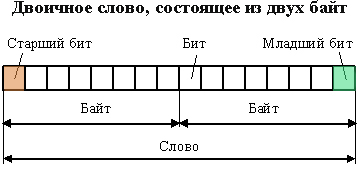
| | + | Также существуют термины, широко используемые в вычислительной сфере - '''бит, байт, слово.''' |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:Slovobit.jpg|480px|Двоичное слово]] |
| | + | |
| | + | <br> |
| | + | |
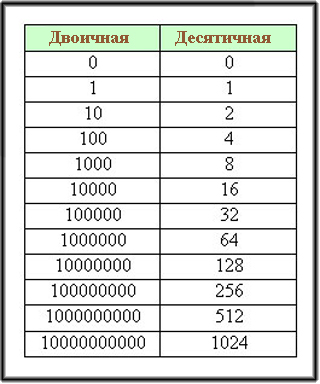
| | + | '''Бит '''– это один двоичный разряд. Крайний слева бит числа - старший разряд (наибольший вес), крайний справа – младший (наименьший вес). |
| | + | |
| | + | Восьмибитовая единица есть байт. |
| | + | |
| | + | Современные компьютеры перерабатывают информацию порциями (словами) по 8, 16 или 32 бита (1, 2 и 4 байта) и т.д. |
| | + | |
| | + | === Перевод чисел из одной системы счисления в другую === |
| | + | |
| | + | <br> |
| | + | |
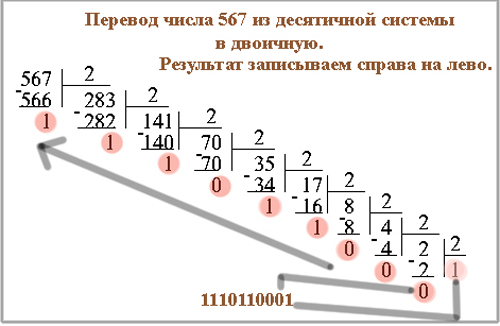
| | + | При переводе чисел, например, из десятичной системы в двоичную, используется метод деления в столбик. Попробуем проделать такую операцию с числом 567. |
| | + | |
| | + | <br> [[Image:Bmb,.jpg|480px|Перевод чисел из одной системы счисления в другую]] |
| | + | |
| | + | <br> |
| | + | |
| | + | При деление 567 на 2 выходит целое 283 и остаток 1. |
| | + | |
| | + | Проведем то же действие с числом 283 - целое 141, остаток 1. |
| | + | |
| | + | Снова делим полученное целое число на 2 - и так до тех пор, пока целое число не станет меньше делителя. |
| | + | |
| | + | А для того, чтобы получить число в двоичной системе счисления, нужно записать последнее целое число (в нашем случае это 1) и приписать к нему все полученные в во время деления остатки в обратном порядке. |
| | + | |
| | + | Выходит, что число в ''десятиричной системе счисления 567 ''будет выглядет в ''двоичной как 1000110111'' |
| | + | |
| | + | === Вопросы === |
| | + | |
| | + | ''1. Что такое система счисления?'' |
| | + | |
| | + | ''2. Позиционные и непозиционные системы счисления.'' |
| | + | |
| | + | ''3. Что представляет собой двоичная система счисления?'' |
| | + | |
| | + | ''4. Каким можно перевести число из десятичной системы в двоичную?'' |
| | + | |
| | + | <br> |
| | + | |
| | + | == Список использованных источников == |
| | + | |
| | + | ''1. Урок на тему: «Системы счисления», Дроводинова Л. В., г. Днепропетровск.'' |
| | + | |
| | + | ''2. Острейковский В.А., Полякова И.В. Информатика. Теория и практика. - Оникс, 2008 г.'' |
| | + | |
| | + | ''3. Андреева Е., Фалина И. Системы счисления и компьютерная арифметика. - Учебное пособие.- БИНОМ, 2004 г.'' |
| | + | |
| | + | ''4. Попов И.И., Партыка Т.Л. Вычислительная техника. – Форум, 2007 г.'' |
| | + | |
| | + | ---- |
| | + | |
| | + | ''<br> Отредактировано и выслано преподавателем Киевского национального университета им. Тараса Шевченка Соловьевым М. С.'' |
| | + | |
| | + | ---- |
| | + | |
| | + | '''Над уроком работали''' |
| | + | |
| | + | Соловьев М. С. |
| | + | |
| | + | Дроводинова Л. В. |
| | + | |
| | + | <br> |
| | + | |
| | + | ---- |
| | + | |
| | + | <br> Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ '''Образовательном форуме'''], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ '''блог,'''] Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ '''Гильдия Лидеров Образования'''] открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.<br> |
| | | | |
| | [[Category:Информатика_9_класс]] | | [[Category:Информатика_9_класс]] |
Но не будем спешить - ведь не все же системы используют такое счисление.
Причина проста – ведь с точки зрения техники машину с двумя состояниями проще создать, причем упрощаются различения этих состояний.
Пример – римские цифры.
И так, как уже было сказано, для компьютера самая подходящая система счисления – двоичная. В такой системе используются лишь два символа - 0 и 1.
И этот метод отлично «дружит» с техническими данными различных цифровых схем. Оказалось, что представлять разные составляющие информации двумя состояниями очень удобно:
Для отображения таких состояний в цифровых системах нужно иметь электросхемы, принимающие два состояния и четко различающие значения электрической величины - потенциала или тока. Каждому из таких значений соответствует или 0 или 1 (обычно «0» представляет низкий уровень потенциала, а «1» – высокий).
Простота создания электросхем с двумя электрическими состояниями и есть причиной того, что двоичное представление чисел «лидирует» в мире современной цифровой техники.
Восьмибитовая единица есть байт.
Современные компьютеры перерабатывают информацию порциями (словами) по 8, 16 или 32 бита (1, 2 и 4 байта) и т.д.
При переводе чисел, например, из десятичной системы в двоичную, используется метод деления в столбик. Попробуем проделать такую операцию с числом 567.
При деление 567 на 2 выходит целое 283 и остаток 1.
Проведем то же действие с числом 283 - целое 141, остаток 1.
Снова делим полученное целое число на 2 - и так до тех пор, пока целое число не станет меньше делителя.
А для того, чтобы получить число в двоичной системе счисления, нужно записать последнее целое число (в нашем случае это 1) и приписать к нему все полученные в во время деления остатки в обратном порядке.
Соловьев М. С.
Дроводинова Л. В.