|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Отрезок, Плоскость, Прямая, Луч</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Отрезок, Плоскость, Прямая, Луч, плоскости, прямые, лучей, отрезок, треугольник</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Плоскость. Прямая. Луч''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Плоскость. Прямая. Луч''' |
| Строка 7: |
Строка 7: |
| | '''Плоскость. Прямая. Луч ''' | | '''Плоскость. Прямая. Луч ''' |
| | | | |
| - | <br>Поверхности стола, школьной доски, оконного стекла дают представление о плоскости. <br>Эти поверхности имеют края. <br>У плоскости края нет. Она безгранично простирается во всех направлениях. <br>Начертим отрезок АВ и продолжим его по линейке в обе стороны (рис. 12). <br>Получим прямую, которую обозначают «прямая АВ» или «прямая ВА». <br>Через любые две точки проходит единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки А и В лежат на прямой. <br> Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке (рис. 13). | + | <br>Поверхности стола, школьной доски, оконного стекла дают представление о '''[[Урок 12. Плоские поверхности. Плоскость|плоскости]]'''. <br>Эти поверхности имеют края. <br>У плоскости края нет. Она безгранично простирается во всех направлениях. <br>Начертим отрезок АВ и продолжим его по линейке в обе стороны (рис. 12). <br>Получим прямую, которую обозначают «прямая АВ» или «прямая ВА». <br>Через любые две точки проходит единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки А и В лежат на прямой. <br> Если две '''[[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|прямые]]''' имеют одну общую точку, то говорят, что они пересекаются в этой точке (рис. 13). |
| | | | |
| | [[Image:15-06-47.jpg|480px|Плоскость. Прямая. Луч]]<br><br>Точка О на рисунке 14 делит прямую на две части. Каждую из этих частей называют лучом. | | [[Image:15-06-47.jpg|480px|Плоскость. Прямая. Луч]]<br><br>Точка О на рисунке 14 делит прямую на две части. Каждую из этих частей называют лучом. |
| Строка 13: |
Строка 13: |
| | Точку О называют началом этих лучей. Конца у луча нет. | | Точку О называют началом этих лучей. Конца у луча нет. |
| | | | |
| - | Лучи на [http://xvatit.com/relax/photoshop-online.php '''рисунке'''] 14 обозначают «луч ОА» и «луч ОБ». Чтобы обозначить луч, называют его начало, а потом какую-нибудь из других точек этого луча. | + | Лучи на [http://xvatit.com/relax/photoshop-online.php '''рисунке'''] 14 обозначают «луч ОА» и «луч ОБ». Чтобы обозначить луч, называют его начало, а потом какую-нибудь из других точек этого луча. |
| | | | |
| | [[Image:15-06-48.jpg|480px|Плоскость. Прямая. Луч]]<br>Точка А (рис. 15) лежит на луче ОА, а точки В и Н на нем не лежат. | | [[Image:15-06-48.jpg|480px|Плоскость. Прямая. Луч]]<br>Точка А (рис. 15) лежит на луче ОА, а точки В и Н на нем не лежат. |
| Строка 19: |
Строка 19: |
| | Лучи, на которые точка разбивает прямую, называют дополнительными друг другу (рис. 14). | | Лучи, на которые точка разбивает прямую, называют дополнительными друг другу (рис. 14). |
| | | | |
| - | <br>''Есть ли края у плоскости? <br>Имеет ли прямая концы? <br>Сколько прямых можно провести через точки М и N? <br>На сколько лучей разбивает прямую MN точка А, лежащая между <br>точками М и N этой прямой? <br>Какой луч дополнителен лучу AM; лучу AN? ''<br><br>75. Отметьте в тетради точки С и D и проведите прямую CD. Отметьте ia отрезке CD точку М. Лежит ли эта точка на прямой CD? Отметьте точку Р на прямой CD, не лежащую на отрезке CD. | + | <br>''Есть ли края у плоскости? <br>Имеет ли прямая концы? <br>Сколько прямых можно провести через точки М и N? <br>На сколько '''[[Порівняння натуральних чисел за допомогою координатного променя. Презентація уроку|лучей]]''' разбивает прямую MN точка А, лежащая между <br>точками М и N этой прямой? <br>Какой луч дополнителен лучу AM; лучу AN? ''<br><br>75. Отметьте в тетради точки С и D и проведите прямую CD. Отметьте ia отрезке CD точку М. Лежит ли эта точка на прямой CD? Отметьте точку Р на прямой CD, не лежащую на отрезке CD. |
| | | | |
| | 76. Начертите прямую и отметьте на ней точки А, Р и С. Запишите 6 различных обозначений прямой. | | 76. Начертите прямую и отметьте на ней точки А, Р и С. Запишите 6 различных обозначений прямой. |
| Строка 25: |
Строка 25: |
| | 77. Какие из точек, обозначенных на рисунке 16, лежат на прямой АВ, i какие точки на ней не лежат? | | 77. Какие из точек, обозначенных на рисунке 16, лежат на прямой АВ, i какие точки на ней не лежат? |
| | | | |
| - | [[Image:15-06-49.jpg|480px|Плоскость. Прямая. Луч]] | + | [[Image:15-06-49.jpg|480px|Плоскость. Прямая. Луч]] |
| | | | |
| | <br>78. Пересекаются ли (рис. 17): | | <br>78. Пересекаются ли (рис. 17): |
| | | | |
| - | прямая АВ и отрезок CD; <br>прямая АВ и луч CD; <br>отрезки АВ и CD; <br>прямые АВ и CD; <br><br>лучи АВ и CD; <br>лучи АВ и ОК; <br>лучи DC и (Ж? <br> | + | прямая АВ и '''[[Отрезок. Длина отрезка. Треугольник|отрезок]]''' CD; <br>прямая АВ и луч CD; <br>отрезки АВ и CD; <br>прямые АВ и CD; <br><br>лучи АВ и CD; <br>лучи АВ и ОК; <br>лучи DC и (Ж? <br> |
| | | | |
| | [[Image:15-06-50.jpg|480px|Плоскость. Прямая. Луч]] | | [[Image:15-06-50.jpg|480px|Плоскость. Прямая. Луч]] |
| Строка 37: |
Строка 37: |
| | 80. На сколько частей делят плоскость две пересекающиеся прямые? | | 80. На сколько частей делят плоскость две пересекающиеся прямые? |
| | | | |
| - | 81. Начертите треугольник ABC. На сколько частей делят плоскость прямые АВ, АС и ВС? | + | 81. Начертите '''[[Задачі до теми Лічба в межах 20. Розв’язування задач на віднімання. Розпізнавання трикутників|треугольник]]''' ABC. На сколько частей делят плоскость прямые АВ, АС и ВС? |
| | | | |
| | 82. По рисунку 16 назовите: 3 точки, 2 отрезка, прямую и 4 луча. | | 82. По рисунку 16 назовите: 3 точки, 2 отрезка, прямую и 4 луча. |
| Строка 51: |
Строка 51: |
| | а) 270 : 9; б) 1224 : 12; в) 300 • 6; г) 801 • 7. | | а) 270 : 9; б) 1224 : 12; в) 300 • 6; г) 801 • 7. |
| | | | |
| - | 87. Может ли сумма двух чисел равняться разности этих же чисел? | + | 87. Может ли [http://xvatit.com/busines/ '''сумма'''] двух чисел равняться разности этих же чисел? |
| | | | |
| | 88. Не выполняя вычислений, определите, сколько цифр будет в частном: | | 88. Не выполняя вычислений, определите, сколько цифр будет в частном: |
| Строка 131: |
Строка 131: |
| | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> | | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | | + | <br> |
| | | | |
| | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 5 класса [[Математика|скачать]]</sub> | | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 5 класса [[Математика|скачать]]</sub> |
Текущая версия на 13:58, 4 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Плоскость. Прямая. Луч
Плоскость. Прямая. Луч
Поверхности стола, школьной доски, оконного стекла дают представление о плоскости.
Эти поверхности имеют края.
У плоскости края нет. Она безгранично простирается во всех направлениях.
Начертим отрезок АВ и продолжим его по линейке в обе стороны (рис. 12).
Получим прямую, которую обозначают «прямая АВ» или «прямая ВА».
Через любые две точки проходит единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки А и В лежат на прямой.
Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке (рис. 13).

Точка О на рисунке 14 делит прямую на две части. Каждую из этих частей называют лучом.
Точку О называют началом этих лучей. Конца у луча нет.
Лучи на рисунке 14 обозначают «луч ОА» и «луч ОБ». Чтобы обозначить луч, называют его начало, а потом какую-нибудь из других точек этого луча.

Точка А (рис. 15) лежит на луче ОА, а точки В и Н на нем не лежат.
Лучи, на которые точка разбивает прямую, называют дополнительными друг другу (рис. 14).
Есть ли края у плоскости?
Имеет ли прямая концы?
Сколько прямых можно провести через точки М и N?
На сколько лучей разбивает прямую MN точка А, лежащая между
точками М и N этой прямой?
Какой луч дополнителен лучу AM; лучу AN?
75. Отметьте в тетради точки С и D и проведите прямую CD. Отметьте ia отрезке CD точку М. Лежит ли эта точка на прямой CD? Отметьте точку Р на прямой CD, не лежащую на отрезке CD.
76. Начертите прямую и отметьте на ней точки А, Р и С. Запишите 6 различных обозначений прямой.
77. Какие из точек, обозначенных на рисунке 16, лежат на прямой АВ, i какие точки на ней не лежат?
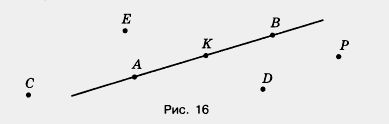
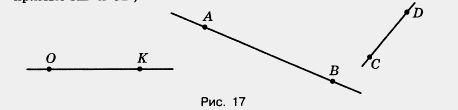
78. Пересекаются ли (рис. 17):
прямая АВ и отрезок CD;
прямая АВ и луч CD;
отрезки АВ и CD;
прямые АВ и CD;
лучи АВ и CD;
лучи АВ и ОК;
лучи DC и (Ж?
79. Отметьте точки А и В на расстоянии 2 см друг от друга. Проведите через эти точки прямую и отложите на ней отрезок АС длиной в 5 см так, чтобы точки В и С были по разные стороны от точки А. Есть ли на прямой точка, находящаяся от точки А на расстоянии 1 см?
80. На сколько частей делят плоскость две пересекающиеся прямые?
81. Начертите треугольник ABC. На сколько частей делят плоскость прямые АВ, АС и ВС?
82. По рисунку 16 назовите: 3 точки, 2 отрезка, прямую и 4 луча.
83. Начертите луч АХ и отложите на нем от его начала один за другим 3 отрезка по 2 см каждый. Можно ли на этом луче отложить 1000 таких отрезков?
84. Вычислите устно:

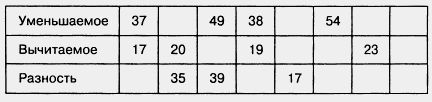
85. Заполните таблицу:
86. Вычислите устно и объясните прием вычислений:
а) 270 : 9; б) 1224 : 12; в) 300 • 6; г) 801 • 7.
87. Может ли сумма двух чисел равняться разности этих же чисел?
88. Не выполняя вычислений, определите, сколько цифр будет в частном:
а) 825 : 5; б) 2952 : 24; в) 11 174 : 37; г) 724 200 : 75.
89. Сложите:
а) 3 м 45 см и 1 м 20 см; в) 2 м 80 см и 4 м 60 см;
б) 7 дм 8 см и 19 см; г) 1 км 250 м и 800 м.
90. Начертите отрезки МР, РК, КС такие, что: МР = 3 см, РК = 2 см 5 мм и КС = 4 см 8 мм.
91. Начертите пятиугольник ABCDE. Отметьте точку М на стороне АВ и точку N на стороне CD. Соедините точки М и N отрезком. Какие получились многоугольники? Назовите их.
92. Выразите:
а) в дециметрах: 50 см; 230 см; 67 м; 800 м;
б) в метрах: 600 см; 30 дм; 2 км; 6 км 50 м; 12 000 мм.
93. Какое число нужно вписать в последнюю клетку цепочки?
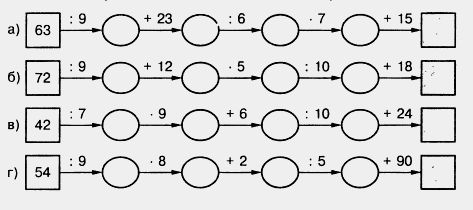
94. Запишите цифрами число:
а) один миллион двести восемьдесят тысяч восемь;
б) один миллиард одна тысяча пятнадцать;
в) двадцать миллиардов двести три миллиона сорок тысяч триста пятьдесят;
г) триста миллиардов пятьдесят миллионов восемьдесят три тысячи пять.
95. Прочитайте числа:
180 000 509; 300 001 700; 608 600 005 003.
96. В правление фирмы входят 5 человек. Из своего состава правление должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Решение. Президентом фирмы можно избрать одного из 5 человек:

После того как президент избран, вице-президентом можно выбрать любого из четырех оставшихся членов правления:

Значит, выбрать президента можно пятью способами, и для каждого выбранного президента четырьмя способами можно выбрать вице-президента. Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5 • 4 = 20 (см. схему на с. 19).
97. Решите задачу:
1) Путь от одной станции до другой товарный поезд прошел за 9 ч, а пассажирский — за 6 ч. Найдите скорость пассажирского поезда, если скорость товарного поезда равна 40 км/ч.
2) От города до села автомашина шла со скоростью 65 км/ч в течение 2 ч. Сколько времени потребуется велосипедисту на этот путь, если он будет двигаться со скоростью 13 км/ч?
98. Выполните действия:
1) 8277 : (3204 : 36);
2) 5238 : (5626 : 58).
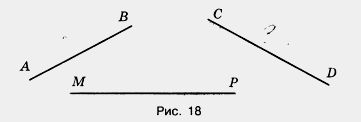
99. С помощью линейки найдите на рисунке 18 точки пересечения прямых АВ и МР, CD и МР, АВ и CD.
100. Начертите прямую и отметьте 3 точки, не лежащие на этой прямой, и 4 точки, лежащие на ней. Обозначьте точки буквами.
101. Начертите луч CD и отметьте 2 точки, не лежащие на нем, и 3 точки, лежащие на этом луче. Точки обозначьте буквами.
102. Начертите луч ОА, отметьте на нем точки М и Р. Запишите все лучи, получившиеся на чертеже.
103. Начертите прямую АВ и отрезки CD, KM и РЕ так, чтобы отрезок CD пересекал прямую АВ, отрезок КМ не пересекал эту прямую, а отрезок РЕ лежал на прямой АВ.
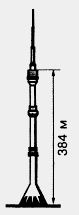
104. Останкинская телевизионная башня в Москве состоит из железобетонной опоры высотой 384 м и металлической части, которая короче этой опорына 229 м. Найдите высоту телевизионной башни.
105. Мотоциклист проехал расстояние от одного города до другого за 3 ч, двигаясь со скоростью 54 км/ч. Сколько времени потребуется мотоциклисту на обратный путь, но уже по другой дороге, если она длиннее первой на 22 км, а его скорость будет меньше прежней на 8 км/ч?
106. Выполните действия:
а) 108 • 55 : 297;
б) 2838 : 86 • 204;
В Древней Русы в качестве единиц измерения длины применялись: косая сажень (248 см) — расстояние от пальцев левой ноги до конца пальцев поднятой провой руки; маховйя сажень (176 см) — расстояние между концами пальцев расставленных в стороны рук; лбкоть (45 см) — расстояние от концов пальцев до локтя согнутой руки.
в) 245 + 315 - 28 • 15;
г) (1237 + 108 - 126) • 61.

107. Выразите в метрах и сантиметрах:
а) высоту терема, равную 3 косым саженям;
б) длину отреза полотна, равную 15 локтям;
в) ширину горницы, равную 2 маховым саженям 3 локтям.
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 5 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|





















