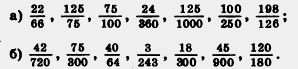KNOWLEDGE HYPERMARKET

Сокращение дробей
 
(3 промежуточные версии не показаны)
Строка 1: Строка 1:
-
<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Сокращение дробей</metakeywords>  
+
<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Сокращение дробей, знаменатель, дробь, десятичные дроби, выражения, натуральных чисел, килограмма</metakeywords>  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 6 класс|Математика 6 класс]]&gt;&gt;Математика: Сокращение дробей'''  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 6 класс|Математика 6 класс]]&gt;&gt;Математика: Сокращение дробей'''  
Строка 5: Строка 5:
<br>  
<br>  
-
'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; 9. Сокращение дробей'''  
+
'''9. Сокращение дробей'''  
-
<br>Если числитель и знаменатель дроби [[Image:17-07-28.jpg]] разделить на 5, то получится равная ей дробь[[Image:17-07-29.jpg]]  
+
<br>Если числитель и '''[[Задачі до уроку на тему «Зведення дробів до спільного знаменника. Порівняння дробів»|знаменатель]]''' дроби [[Image:17-07-28.jpg]] разделить на 5, то получится равная ей дробь[[Image:17-07-29.jpg|Дробь]]  
'''''Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.'''''  
'''''Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.'''''  
-
Дробь [[Image:17-07-30.jpg]] сократить нельзя, так как числа 3 и 4 — взаимно простые числа. Такую дробь называют '''''несократимой'''''. <br>Наибольшее число, на которое можно сократить дробь, это наибольший общий делитель ее числителя и знаменателя. Например, наибольшим общим делителем чисел 150 и 225 является 75. Значит, дробь&nbsp;[[Image:17-07-31.jpg]] межно сократить на 75, получим [[Image:17-07-32.jpg]]&nbsp; &nbsp;.<br>Тот же ответ можно получить, сокращая дробь [[Image:17-07-31.jpg]] последовательно на общие делители чисел 150 и 225, используя для их&nbsp; нахождения признаки делимости:[[Image:17-07-33.jpg]]<br>Иногда удобно при сокращении дроби разложить числитель и знаменатель на несколько множителей, а потом уже сократить.
+
Дробь [[Image:17-07-30.jpg]] сократить нельзя, так как числа 3 и 4 — взаимно простые числа. Такую дробь называют несократимой. <br>Наибольшее число, на которое можно сократить дробь, это наибольший общий делитель ее числителя и знаменателя. Например, наибольшим общим делителем чисел 150 и 225 является 75. Значит, дробь&nbsp;[[Image:17-07-31.jpg]] межно сократить на 75, получим [[Image:17-07-32.jpg]]&nbsp; &nbsp;.<br>Тот же ответ можно получить, сокращая дробь [[Image:17-07-31.jpg]] последовательно на общие делители чисел 150 и 225, используя для их&nbsp; нахождения признаки делимости:[[Image:17-07-33.jpg|120px|Дробь]]<br>Иногда удобно при сокращении дроби разложить числитель и знаменатель на несколько множителей, а потом уже сократить.  
-
Например,&nbsp;[[Image:17-07-34.jpg]]&nbsp; &nbsp;Сократим на З • З • 5 и&nbsp; получим [[Image:17-07-35.jpg]]  
+
Например,&nbsp;[[Image:17-07-34.jpg|180px|Задание]]&nbsp; &nbsp;Сократим на З • З • 5 и&nbsp; получим [[Image:17-07-35.jpg|320px|Задание]]  
-
&nbsp;'''?''' Что называют сокращением дроби? Какую дробь называют несократимой?
+
&nbsp;'''?''' Что называют сокращением дроби? Какую '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|дробь]]''' называют несократимой?  
-
'''К '''232.Сократите дроби:[[Image:Сократите дроби:]]
+
'''К '''232.Сократите дроби:[[Image:17-07-52.jpg|160px|Задание]]  
-
233.&nbsp;&nbsp; &nbsp;Сократите дроби:[[Image:17-07-37.jpg]]<br>234.&nbsp;&nbsp; &nbsp;Сократите:[[Image:17-07-38.jpg]]<br>235.&nbsp;&nbsp; &nbsp;Представьте в виде обыкновенной несократимой дроби: 0,2; 0,8; 0,5; 0,15; 0,24; 0,35; 0,75; 0,05; 0,125; 0,025; 0,008; 0,375.<br>236.&nbsp;&nbsp; &nbsp;Какую часть часа составляют 45 мин, 12 мин, 15 мин, 40 мин, 35 мин?<br>237.&nbsp;&nbsp; &nbsp;Какую часть развернутого угла составляют 30°, 45°, 60°, 90°, 120°, 135°, 150°?<br>238.&nbsp;&nbsp; &nbsp;Какую часть килограмма составляют 125 г, 250 г, 750 г?<br>239.&nbsp;&nbsp; &nbsp;Выполните действие:[[Image:17-07-39.jpg]]<br>240. Один рабочий изготовил 16 одинаковых деталей за 6 ч, а другой 24 такие же детали за 15 ч. Какой из них тратил на изготовление одной детали больше времени и на сколько?
+
233.&nbsp;&nbsp; &nbsp;Сократите дроби:[[Image:17-07-37.jpg|320px|Задание]]<br>234.&nbsp;&nbsp; &nbsp;Сократите:[[Image:17-07-38.jpg|460px|Задание]]<br>235.&nbsp;&nbsp; &nbsp;Представьте в виде обыкновенной несократимой дроби: 0,2; 0,8; 0,5; 0,15; 0,24; 0,35; 0,75; 0,05; 0,125; 0,025; 0,008; 0,375.<br>236.&nbsp;&nbsp; &nbsp;Какую часть часа составляют 45 мин, 12 мин, 15 мин, 40 мин, 35 мин?<br>237.&nbsp;&nbsp; &nbsp;Какую часть развернутого угла составляют 30°, 45°, 60°, 90°, 120°, 135°, 150°?<br>238.&nbsp;&nbsp; &nbsp;Какую часть '''[[Міри маси. Грам|килограмма]]''' составляют 125 г, 250 г, 750 г?<br>239.&nbsp;&nbsp; &nbsp;Выполните действие:[[Image:17-07-39.jpg|460px|Задание]]<br>240. Один рабочий изготовил 16 одинаковых деталей за 6 ч, а другой 24 такие же детали за 15 ч. Какой из них тратил на изготовление одной детали больше времени и на сколько?  
-
241. Из 20 м ткани сшили 8 одинаковых платьев для взрослых, а из 12 м сшили 8 детских платьев. Сколько метров ткани пошло на одно детское платье и сколько на одно платье для взрослых?
+
241. Из 20 м ткани сшили 8 одинаковых платьев для взрослых, а из 12 м сшили 8 детских платьев. Сколько метров ткани пошло на одно детское платье и сколько на одно платье для взрослых?  
-
242. Применив распределительный закон, представьте числитель дроби в виде произведения, а затем сократите: <br>[[Image:17-07-40.jpg]]<br>&nbsp;&nbsp; <br>'''П''' 243. Вычислите устно:
+
242. Применив распределительный закон, представьте числитель дроби в виде произведения, а затем сократите: <br>[[Image:17-07-40.jpg|460px|Задание]]<br>&nbsp;&nbsp; <br>'''П''' 243. Вычислите устно:  
-
[[Image:17-07-41.jpg]]
+
[[Image:17-07-41.jpg|480px|Задание]]  
-
а) 450 • 2 б) 364 + 116 в) 20 • 0,5<br>-250&nbsp;&nbsp; &nbsp;: 6 -2,5<br>: 13&nbsp;&nbsp; &nbsp;+70&nbsp;: 1,5<br>4,8&nbsp;: 2 + 0,8&nbsp;: 0,4 • 0,2<br>• 7&nbsp;&nbsp; &nbsp;-8 • 0,12<br>Д) 3-0,4&nbsp;: 0,13 • 0,1&nbsp;: 0,2 <br><br>&nbsp; <br>245.Найдите среди чисел 1, 3, 10, 12, 13, 15, 16, 39 пары взаимно простых чисел.<br>246.&nbsp; Найдите равные среди чисел:[[Image:17-07-42.jpg]]
+
а) 450 • 2 б) 364 + 116 в) 20 • 0,5<br>-250&nbsp;&nbsp; &nbsp;: 6 -2,5<br>: 13&nbsp;&nbsp; &nbsp;+70&nbsp;: 1,5<br>4,8&nbsp;: 2 + 0,8&nbsp;: 0,4 • 0,2<br>• 7&nbsp;&nbsp; &nbsp;-8 • 0,12<br>Д) 3-0,4&nbsp;: 0,13 • 0,1&nbsp;: 0,2 <br>&nbsp; <br>245.Найдите среди чисел 1, 3, 10, 12, 13, 15, 16, 39 пары взаимно простых чисел.<br>246.&nbsp; Найдите равные среди чисел:[[Image:17-07-42.jpg|320px|Задание]]  
-
247. При каких натуральных значениях буквы равны дроби:[[Image:17-07-43.jpg]]
+
247. При каких натуральных значениях буквы равны дроби:[[Image:17-07-43.jpg|320px|Задание]]  
-
248. В бригаде 5 рабочих. Зарплата первого рабочего увеличилась на 10%, второго — на 20%, третьего — на 30%, а у <br>четвертого и пятого осталась прежней. На сколько процентов в среднем выросла зарплата рабочего этой бригады, если раньше все они имели одинаковую зарплату?
+
248. В бригаде 5 рабочих. Зарплата первого рабочего увеличилась на 10%, второго — на 20%, третьего — на 30%, а у четвертого и пятого осталась прежней. На сколько процентов в среднем выросла [http://xvatit.com/busines/jobs-career/ '''зарплата'''] рабочего этой бригады, если раньше все они имели одинаковую зарплату?  
-
'''А''' 249. Древнегреческих, а также древнеиндийских матема- ВЭ1 тиков интересовали числа, которые соответствовали количеству точек, расположенных в виде некоторой геометрической фигуры — треугольника, квадрата и др. Такие числа называли фигурными. Например, число 10 называли треугольным, число 16 — квадратным (рис. 13).  
+
'''А''' 249. Древнегреческих, а также древнеиндийских математиков интересовали числа, которые соответствовали количеству точек, расположенных в виде некоторой геометрической фигуры — треугольника, квадрата и др. Такие числа называли фигурными. Например, число 10 называли треугольным, число 16 — квадратным (рис. 13).  
-
[[Image:17-07-44.jpg]]
+
[[Image:17-07-44.jpg|240px|Задание]]  
-
Такое представление помогало древним ученым изучать свойства чисел. Используя рисунок 13, попробуйте найти еще несколько треугольных и квадратных чисел. Какими свойствами обладают эти числа? Подумайте, как можно находить треугольные и квадратные числа, используя ряд натуральных чисел.
+
Такое представление помогало древним ученым изучать свойства чисел. Используя рисунок 13, попробуйте найти еще несколько треугольных и квадратных чисел. Какими свойствами обладают эти числа? Подумайте, как можно находить треугольные и квадратные числа, используя ряд '''[[Обозначение натуральных чисел|натуральных чисел]]'''.  
-
250.&nbsp;&nbsp; &nbsp;Разделите числитель и знаменатель дроби:
+
250.&nbsp;&nbsp; &nbsp;Разделите числитель и знаменатель дроби:  
-
[[Image:17-07-45.jpg]]<br><br>251.&nbsp;&nbsp; &nbsp;Умножьте числитель и знаменатель дроби:
+
[[Image:17-07-45.jpg|420px|Задание]]<br><br>251.&nbsp;&nbsp; &nbsp;Умножьте числитель и знаменатель дроби:  
-
[[Image:17-07-46.jpg]]
+
[[Image:17-07-46.jpg|420px|Задание]]  
-
252.&nbsp;&nbsp; &nbsp;Собственная скорость катера 12,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите скорость катера по течению и против течения.
+
252.&nbsp;&nbsp; &nbsp;Собственная скорость катера 12,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите скорость катера по течению и против течения.  
-
253.&nbsp;&nbsp; &nbsp;Скорость движения теплохода по течению реки 22,7 км/ч. Скорость течения 1,9 км/ч. Найдите собственную скорость теплохода и его скорость против течения.
+
253.&nbsp;&nbsp; &nbsp;Скорость движения теплохода по течению реки 22,7 км/ч. Скорость течения 1,9 км/ч. Найдите собственную скорость теплохода и его скорость против течения.  
-
254.&nbsp;&nbsp; &nbsp;Бригада изготовила за 3 дня 6000 деталей при плане 5100 деталей. Причем в первый день была изготовлена треть всех выпущенных деталей, а во второй день[[Image:17-07-47.jpg]] плана. Сколько деталей изготовила бригада в третий день?
+
254.&nbsp;&nbsp; &nbsp;Бригада изготовила за 3 дня 6000 деталей при плане 5100 деталей. Причем в первый день была изготовлена треть всех выпущенных деталей, а во второй день[[Image:17-07-47.jpg]] плана. Сколько деталей изготовила бригада в третий день?  
-
255.&nbsp;&nbsp; &nbsp;Найдите значение выражения:
+
255.&nbsp;&nbsp; &nbsp;Найдите значение '''[[Повторення таблиць додавання і віднімання. Складання виразів за текстовим формулюванням|выражения]]''':  
-
[[Image:17-07-48.jpg]]
+
[[Image:17-07-48.jpg|320px|Задание]]  
-
<br>256. Решите задачу:
+
<br>256. Решите задачу:  
-
1)&nbsp;&nbsp; &nbsp;Путешественник проплыл протйв течения реки на моторной лодке 3 ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч?
+
1)&nbsp;&nbsp; &nbsp;Путешественник проплыл против течения реки на моторной лодке 3 ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч?  
-
2)&nbsp;&nbsp; &nbsp;Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28 км/ч. Сколько времени затратил путешественник на обратный путь?
+
2)&nbsp;&nbsp; &nbsp;Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28 км/ч. Сколько времени затратил путешественник на обратный путь?  
-
'''Д '''257. Сократите дроби:
+
'''Д '''257. Сократите дроби:  
-
[[Image:17-07-49.jpg]]<br><br>258 Сокоатите [[Image:17-07-50.jpg]]<br>259.&nbsp;&nbsp; &nbsp;Представьте в виде обыкновенной несократимой дроби следующие десятичные дроби: 0,875; 0,75; 0,035.<br>260.&nbsp;&nbsp; &nbsp;Выполните действие и сократите результат:[[Image:17-07-51.jpg]]<br>261.&nbsp;&nbsp; &nbsp;Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.
+
[[Image:17-07-49.jpg|480px|Задание]]<br><br>258 Сокоатите [[Image:17-07-50.jpg|180px|Задание]]<br>259.&nbsp;&nbsp; &nbsp;Представьте в виде обыкновенной несократимой дроби следующие '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичные дроби]]''': 0,875; 0,75; 0,035.<br>260.&nbsp;&nbsp; &nbsp;Выполните действие и сократите результат:[[Image:17-07-51.jpg|420px|Задание]]<br>261.&nbsp;&nbsp; &nbsp;Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.  
-
262.&nbsp;&nbsp; &nbsp;За 4 кг конфет и 3 кг печенья заплатили 12 р. 20 к. За 2 кг таких же конфет и 3 кг такого же печенья заплатили 8 р. 20 к. Сколько стоит 1 кг печенья?
+
262.&nbsp;&nbsp; &nbsp;За 4 кг конфет и 3 кг печенья заплатили 12 р. 20 к. За 2 кг таких же конфет и 3 кг такого же печенья заплатили 8 р. 20 к. Сколько стоит 1 кг печенья?  
-
263.&nbsp;&nbsp; &nbsp;Выполните действия:
+
263.&nbsp;&nbsp; &nbsp;Выполните действия:  
-
а) (867 000:2125-396,4) • 2,15;
+
а) (867 000:2125-396,4) • 2,15;  
-
б) (26,16:6 + 2,6 • 1,4):0,4-0,4.<br><br><br><br><br>  
+
б) (26,16:6 + 2,6 • 1,4):0,4-0,4.<br>  
<br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br>  
<br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br>  
-
<sub>Учебники и книги по всему предметам, домашняя работа, [[Гипермаркет знаний - первый в мире!|онлайн]] библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 6 класса [[Математика|скачать]]</sub>
 
-
<br>  
+
 
 +
<sub>Учебники и книги по всему предметам, домашняя работа, [[Гипермаркет знаний - первый в мире!|онлайн]] библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 6 класса [[Математика|скачать]]</sub><br>  
  '''<u>Содержание урока</u>'''
  '''<u>Содержание урока</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока'''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока'''
-
  [[Image:1236084776 kr.jpg|10x10px]] опорный каркас   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас   
-
  [[Image:1236084776 kr.jpg|10x10px]] презентация урока
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
-
  [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы  
-
  [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии  
   
   
  '''<u>Практика</u>'''
  '''<u>Практика</u>'''
-
  [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения  
-
  [[Image:1236084776 kr.jpg|10x10px]] самопроверка
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
-
  [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
-
  [[Image:1236084776 kr.jpg|10x10px]] домашние задания
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
-
  [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
-
  [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
-
 
+
  '''<u>Иллюстрации</u>'''
  '''<u>Иллюстрации</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
-
  [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки  
-
  [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
-
  [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
-
  [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
   
   
  '''<u>Дополнения</u>'''
  '''<u>Дополнения</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
-
  [[Image:1236084776 kr.jpg|10x10px]] статьи  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи  
-
  [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных  
-
  [[Image:1236084776 kr.jpg|10x10px]] шпаргалки  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки  
-
  [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
-
  [[Image:1236084776 kr.jpg|10x10px]] словарь терминов                           
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов                           
-
  [[Image:1236084776 kr.jpg|10x10px]] прочие  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие  
  '''<u></u>'''
  '''<u></u>'''
  <u>Совершенствование учебников и уроков
  <u>Совершенствование учебников и уроков
-
  </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
+
  </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
-
  [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике  
-
  [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке  
-
  [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми  
-
 
+
  '''<u>Только для учителей</u>'''
  '''<u>Только для учителей</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
-
  [[Image:1236084776 kr.jpg|10x10px]] календарный план на год   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год   
-
  [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации   
-
  [[Image:1236084776 kr.jpg|10x10px]] программы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
-
  [[Image:1236084776 kr.jpg|10x10px]] обсуждения
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
   
   
   
   

Текущая версия на 09:53, 7 октября 2012

Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Сокращение дробей


9. Сокращение дробей


Если числитель и знаменатель дроби 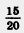17-07-28.jpg разделить на 5, то получится равная ей дробь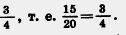Дробь

Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.

Дробь 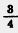17-07-30.jpg сократить нельзя, так как числа 3 и 4 — взаимно простые числа. Такую дробь называют несократимой.
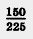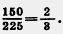Наибольшее число, на которое можно сократить дробь, это наибольший общий делитель ее числителя и знаменателя. Например, наибольшим общим делителем чисел 150 и 225 является 75. Значит, дробь 17-07-31.jpg межно сократить на 75, получим 17-07-32.jpg   .
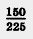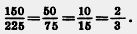
Тот же ответ можно получить, сокращая дробь 17-07-31.jpg последовательно на общие делители чисел 150 и 225, используя для их  нахождения признаки делимости:Дробь
Иногда удобно при сокращении дроби разложить числитель и знаменатель на несколько множителей, а потом уже сократить.

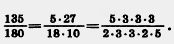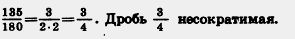
Например, Задание   Сократим на З • З • 5 и  получим Задание

 ? Что называют сокращением дроби? Какую дробь называют несократимой?

К 232.Сократите дроби: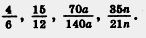Задание

233.    Сократите дроби: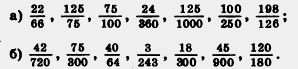Задание
234.    Сократите: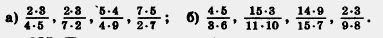Задание
235.    Представьте в виде обыкновенной несократимой дроби: 0,2; 0,8; 0,5; 0,15; 0,24; 0,35; 0,75; 0,05; 0,125; 0,025; 0,008; 0,375.
236.    Какую часть часа составляют 45 мин, 12 мин, 15 мин, 40 мин, 35 мин?
237.    Какую часть развернутого угла составляют 30°, 45°, 60°, 90°, 120°, 135°, 150°?
238.    Какую часть килограмма составляют 125 г, 250 г, 750 г?
239.    Выполните действие: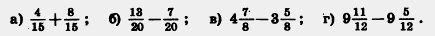Задание
240. Один рабочий изготовил 16 одинаковых деталей за 6 ч, а другой 24 такие же детали за 15 ч. Какой из них тратил на изготовление одной детали больше времени и на сколько?

241. Из 20 м ткани сшили 8 одинаковых платьев для взрослых, а из 12 м сшили 8 детских платьев. Сколько метров ткани пошло на одно детское платье и сколько на одно платье для взрослых?

242. Применив распределительный закон, представьте числитель дроби в виде произведения, а затем сократите:
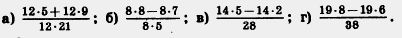
Задание
  
П 243. Вычислите устно:

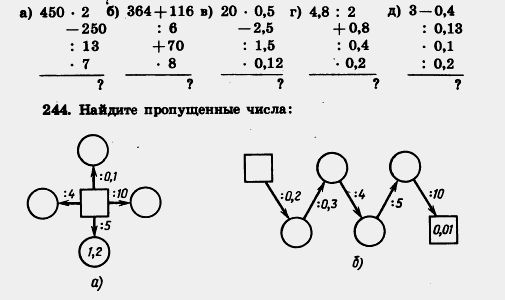
Задание

а) 450 • 2 б) 364 + 116 в) 20 • 0,5
-250    : 6 -2,5
: 13    +70 : 1,5
4,8 : 2 + 0,8 : 0,4 • 0,2
• 7    -8 • 0,12
Д) 3-0,4 : 0,13 • 0,1 : 0,2
 
245.Найдите среди чисел 1, 3, 10, 12, 13, 15, 16, 39 пары взаимно простых чисел.
246.  Найдите равные среди чисел: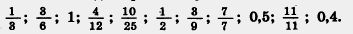Задание

247. При каких натуральных значениях буквы равны дроби: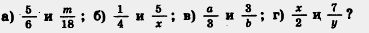Задание

248. В бригаде 5 рабочих. Зарплата первого рабочего увеличилась на 10%, второго — на 20%, третьего — на 30%, а у четвертого и пятого осталась прежней. На сколько процентов в среднем выросла зарплата рабочего этой бригады, если раньше все они имели одинаковую зарплату?

А 249. Древнегреческих, а также древнеиндийских математиков интересовали числа, которые соответствовали количеству точек, расположенных в виде некоторой геометрической фигуры — треугольника, квадрата и др. Такие числа называли фигурными. Например, число 10 называли треугольным, число 16 — квадратным (рис. 13).

Задание

Такое представление помогало древним ученым изучать свойства чисел. Используя рисунок 13, попробуйте найти еще несколько треугольных и квадратных чисел. Какими свойствами обладают эти числа? Подумайте, как можно находить треугольные и квадратные числа, используя ряд натуральных чисел.

250.    Разделите числитель и знаменатель дроби:

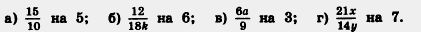
Задание

251.    Умножьте числитель и знаменатель дроби:

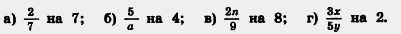
Задание

252.    Собственная скорость катера 12,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите скорость катера по течению и против течения.

253.    Скорость движения теплохода по течению реки 22,7 км/ч. Скорость течения 1,9 км/ч. Найдите собственную скорость теплохода и его скорость против течения.

254.    Бригада изготовила за 3 дня 6000 деталей при плане 5100 деталей. Причем в первый день была изготовлена треть всех выпущенных деталей, а во второй день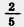17-07-47.jpg плана. Сколько деталей изготовила бригада в третий день?

255.    Найдите значение выражения:

Задание


256. Решите задачу:

1)    Путешественник проплыл против течения реки на моторной лодке 3 ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч?

2)    Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28 км/ч. Сколько времени затратил путешественник на обратный путь?

Д 257. Сократите дроби:

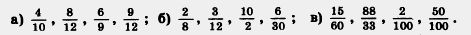
Задание

258 Сокоатите 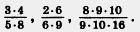Задание
259.    Представьте в виде обыкновенной несократимой дроби следующие десятичные дроби: 0,875; 0,75; 0,035.
260.    Выполните действие и сократите результат: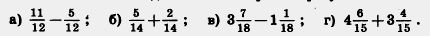Задание
261.    Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.

262.    За 4 кг конфет и 3 кг печенья заплатили 12 р. 20 к. За 2 кг таких же конфет и 3 кг такого же печенья заплатили 8 р. 20 к. Сколько стоит 1 кг печенья?

263.    Выполните действия:

а) (867 000:2125-396,4) • 2,15;

б) (26,16:6 + 2,6 • 1,4):0,4-0,4.


Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы


Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 6 класса скачать

Содержание урока
1236084776 kr.jpg конспект урока
1236084776 kr.jpg опорный каркас  
1236084776 kr.jpg презентация урока
1236084776 kr.jpg акселеративные методы 
1236084776 kr.jpg интерактивные технологии 

Практика
1236084776 kr.jpg задачи и упражнения 
1236084776 kr.jpg самопроверка
1236084776 kr.jpg практикумы, тренинги, кейсы, квесты
1236084776 kr.jpg домашние задания
1236084776 kr.jpg дискуссионные вопросы
1236084776 kr.jpg риторические вопросы от учеников

Иллюстрации
1236084776 kr.jpg аудио-, видеоклипы и мультимедиа 
1236084776 kr.jpg фотографии, картинки 
1236084776 kr.jpg графики, таблицы, схемы
1236084776 kr.jpg юмор, анекдоты, приколы, комиксы
1236084776 kr.jpg притчи, поговорки, кроссворды, цитаты

Дополнения
1236084776 kr.jpg рефераты
1236084776 kr.jpg статьи 
1236084776 kr.jpg фишки для любознательных 
1236084776 kr.jpg шпаргалки 
1236084776 kr.jpg учебники основные и дополнительные
1236084776 kr.jpg словарь терминов                          
1236084776 kr.jpg прочие 

Совершенствование учебников и уроков
1236084776 kr.jpg исправление ошибок в учебнике
1236084776 kr.jpg обновление фрагмента в учебнике 
1236084776 kr.jpg элементы новаторства на уроке 
1236084776 kr.jpg замена устаревших знаний новыми 

Только для учителей
1236084776 kr.jpg идеальные уроки 
1236084776 kr.jpg календарный план на год  
1236084776 kr.jpg методические рекомендации  
1236084776 kr.jpg программы
1236084776 kr.jpg обсуждения


Интегрированные уроки


Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%A1%D0%BE%D0%BA%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B4%D1%80%D0%BE%D0%B1%D0%B5%D0%B9»

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: