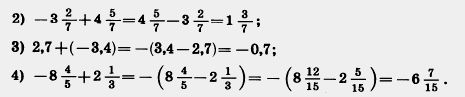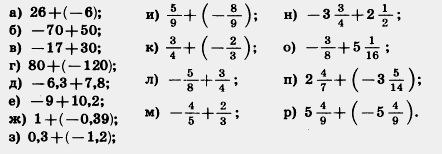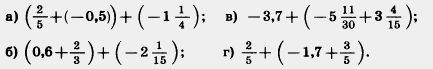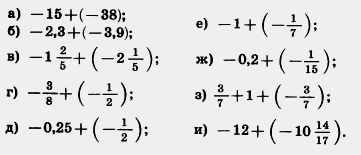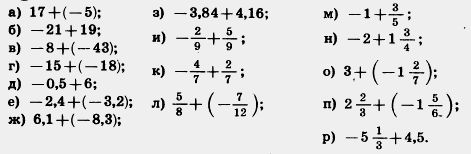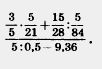|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' 33. Сложение чисел с разными знаками'''<br><br>Если температура воздуха была равна 9 °С, а потом она изменилась на — 6 °С (т. е. понизилась на 6 °С), то она стала равной 9 + (— 6) градусам (рис. 83). <br>Чтобы сложить числа 9 и — 6 с помощью координатной прямой, надо точку А (9) переместить влево на 6 единичных отрезков (рис. 84). Получим точку В (3).<br><br>[[Image:21-07-280.jpg]] <br>Значит, 9+( — 6) = 3. Число 3 имеет тот же знак, что и слагаемое 9, а его модуль равен разности модулей слагаемых 9 и —6. | + | '''33. Сложение чисел с разными знаками'''<br><br>Если температура воздуха была равна 9 °С, а потом она изменилась на — 6 °С (т. е. понизилась на 6 °С), то она стала равной 9 + (— 6) градусам (рис. 83). |
| | + | |
| | + | Чтобы сложить числа 9 и — 6 с помощью координатной прямой, надо точку А (9) переместить влево на 6 единичных отрезков (рис. 84). Получим точку В (3).<br><br>[[Image:21-07-280.jpg|480px|Задание]] |
| | + | |
| | + | Значит, 9+( — 6) = 3. Число 3 имеет тот же знак, что и слагаемое 9, а его модуль равен разности модулей слагаемых 9 и —6. |
| | | | |
| | Действительно, |3| =3 и |9| — |— 6| = = 9 — 6 = 3. | | Действительно, |3| =3 и |9| — |— 6| = = 9 — 6 = 3. |
| | | | |
| - | [[Image:21-07-281.jpg]] | + | [[Image:21-07-281.jpg|120px|Задание]] |
| | | | |
| | Если та же температура воздуха 9 °С изменилась на —12 °С (т. е. понизилась на 12 °С), то она стала равной 9 +( —12) градусам (рис. 85). Сложив числа 9 и —12 с помощью координатной прямой (рис. 86), получим 9 + ( —12)= —3. Число —3 имеет тот же знак, что и слагаемое —12, а его модуль равен разности модулей слагаемых —12 и 9. | | Если та же температура воздуха 9 °С изменилась на —12 °С (т. е. понизилась на 12 °С), то она стала равной 9 +( —12) градусам (рис. 85). Сложив числа 9 и —12 с помощью координатной прямой (рис. 86), получим 9 + ( —12)= —3. Число —3 имеет тот же знак, что и слагаемое —12, а его модуль равен разности модулей слагаемых —12 и 9. |
| Строка 15: |
Строка 19: |
| | Действительно, | — 3| = 3 и | —12| — | —9| =12 — 9 = 3. | | Действительно, | — 3| = 3 и | —12| — | —9| =12 — 9 = 3. |
| | | | |
| - | '''''Чтобы сложить два числа с разными знаками, надо: 1) из большего модуля слагаемых вычесть меньший; 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.''''' | + | '''''Чтобы сложить два числа с разными знаками, надо:''''' |
| | + | |
| | + | '''''1) из большего модуля слагаемых вычесть меньший;''''' |
| | + | |
| | + | '''''2) поставить перед полученным числом знак того слагаемого, модуль которого больше.''''' |
| | | | |
| | Обычно сначала определяют и записывают знак суммы, а потом находят разность модулей. | | Обычно сначала определяют и записывают знак суммы, а потом находят разность модулей. |
| | | | |
| - | [[Image:21-07-282.jpg]]<br><br>Например:<br>1) 6,1+(— 4,2)= +(6,1 — 4,2)= 1,9,<br>или короче 6,1+( — 4,2) = 6,1 — 4,2 = 1,9; | + | [[Image:21-07-282.jpg|480px|Задание]]<br><br>Например: |
| | | | |
| - | [[Image:21-07-283.jpg]]<br><br>При сложении положительных и отрицательных чисел можно использовать микрокалькулятор. Чтобы ввести отрицательное число в микрокалькулятор, надо ввести модуль этого числа, потом нажать клавишу «изменение знака» |/—/|. Например, чтобы ввести число —56,81, надо последовательно нажимать клавиши: | 5 |, | 6 |, | ¦ |, | 8 |, | 1 |, |/—/|. Операции над числами любого знака выполняются на микрокалькуляторе так же, как над положительными числами.<br>Например, сумму —6,1 + 3,8 вычисляют по программе
| + | 1) 6,1+(— 4,2)= +(6,1 — 4,2)= 1,9,<br>или короче 6,1+( — 4,2) = 6,1 — 4,2 = 1,9; |
| | | | |
| - | [[Image:21-07-284.jpg]]<br><br>''' ?''' Числа а и b имеют разные знаки. Какой знак будет иметь сумма этих чисел, если больший модуль имеет отрицательное число? если меньший модуль имеет отрицательное число? если больший модуль имеет положительное число? если меньший модуль имеет положительное число? Сформулируйте правило сложения чисел с разными знаками. Как ввести в микрокалькулятор отрицательное число?<br><br>''' К''' 1045. Число 6 изменили на —10. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 6 и —10? | + | [[Image:21-07-283.jpg|480px|Задание]]<br><br>При сложении положительных и отрицательных чисел можно использовать микрокалькулятор. Чтобы ввести отрицательное число в микрокалькулятор, надо ввести модуль этого числа, потом нажать клавишу «изменение знака» |/—/|. Например, чтобы ввести число —56,81, надо последовательно нажимать клавиши: | 5 |, | 6 |, | ¦ |, | 8 |, | 1 |, |/—/|. Операции над числами любого знака выполняются на микрокалькуляторе так же, как над положительными числами. |
| | + | |
| | + | Например, сумму —6,1 + 3,8 вычисляют по [http://xvatit.com/it/fishki-ot-itshki/ '''[[программе]]'''] |
| | + | |
| | + | |
| | + | [[Image:21-07-284.jpg|480px|Задание]]<br><br>''''' ?''' Числа а и b имеют разные знаки. Какой знак будет иметь сумма этих чисел, если больший модуль имеет отрицательное число?'' |
| | + | |
| | + | ''если меньший модуль имеет отрицательное число? '' |
| | + | |
| | + | ''если больший модуль имеет положительное число? '' |
| | + | |
| | + | ''если меньший модуль имеет положительное число? '' |
| | + | |
| | + | ''Сформулируйте правило сложения чисел с разными знаками. Как ввести в микрокалькулятор отрицательное число?''<br><br>'''К''' 1045. Число 6 изменили на —10. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна [http://xvatit.com/busines/ '''сумма'''] 6 и —10? |
| | | | |
| | 1046. Число 10 изменили на —6. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 10 и -6? | | 1046. Число 10 изменили на —6. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 10 и -6? |
| Строка 35: |
Строка 56: |
| | 1050. Выполните сложение: | | 1050. Выполните сложение: |
| | | | |
| - | [[Image:21-07-285.jpg]]<br><br>1051. Прибавьте: | + | [[Image:21-07-285.jpg|480px|Задание]]<br><br>1051. Прибавьте: |
| | | | |
| | а) к сумме —6 и —12 число 20;<br>б) к числу 2,6 сумму —1,8 и 5,2;<br>в) к сумме —10 и —1,3 сумму 5 и 8,7;<br>г) к сумме 11 и —6,5 сумму —3,2 и —6. | | а) к сумме —6 и —12 число 20;<br>б) к числу 2,6 сумму —1,8 и 5,2;<br>в) к сумме —10 и —1,3 сумму 5 и 8,7;<br>г) к сумме 11 и —6,5 сумму —3,2 и —6. |
| Строка 47: |
Строка 68: |
| | 1054. Найдите значение выражения: | | 1054. Найдите значение выражения: |
| | | | |
| - | [[Image:21-07-286.jpg]] | + | [[Image:21-07-286.jpg|480px|Задание]] |
| | | | |
| | <br>1055. Выполните действия с помощью микрокалькулятора: | | <br>1055. Выполните действия с помощью микрокалькулятора: |
| Строка 53: |
Строка 74: |
| | а) — 3,2579 + ( —12,308); г) -3,8564+ (-0,8397) +7,84;<br>б) 7,8547+ ( — 9,239); д) -0,083 + (-6,378) + 3,9834;<br>в) —0,00154 + 0,0837; е) —0,0085+ 0,00354+ ( — 0,00921). <br><br>'''П''' 1056. Найдите значение суммы: | | а) — 3,2579 + ( —12,308); г) -3,8564+ (-0,8397) +7,84;<br>б) 7,8547+ ( — 9,239); д) -0,083 + (-6,378) + 3,9834;<br>в) —0,00154 + 0,0837; е) —0,0085+ 0,00354+ ( — 0,00921). <br><br>'''П''' 1056. Найдите значение суммы: |
| | | | |
| - | [[Image:21-07-287.jpg]]<br><br>1057. Найдите значение выражения: | + | [[Image:21-07-287.jpg|320px|Задание]]<br><br>1057. Найдите значение выражения: |
| | | | |
| - | [[Image:21-07-288.jpg]]<br><br>1058. Сколько целых чисел расположено между числами: | + | [[Image:21-07-288.jpg|480px|Задание]]<br><br>1058. Сколько целых чисел расположено между числами: |
| | | | |
| | а) 0 и 24; б) —12 и —3; в) —20 и 7? | | а) 0 и 24; б) —12 и —3; в) —20 и 7? |
| Строка 69: |
Строка 90: |
| | '''М''' 1061. Радиусы географических параллелей земной поверхности, на которых расположены города Афины и Москва, соответственно равны 5040 км и 3580 км (рис. 87). На сколько параллель Москвы короче параллели Афин? | | '''М''' 1061. Радиусы географических параллелей земной поверхности, на которых расположены города Афины и Москва, соответственно равны 5040 км и 3580 км (рис. 87). На сколько параллель Москвы короче параллели Афин? |
| | | | |
| - | [[Image:21-07-289.jpg]]<br><br>1062. Составьте уравнение для решения задачи: «Поле площадью 2,4 га разделили на два участка. Найдите площадь каждого участка, если известно, что один из участков: <br>а) на 0,8 га больше другого;<br>б) на 0,2 га меньше другого;<br>в) в 3 раза больше другого;<br>г) в 1,5 раза меньше другого;<br>д) составляет [[Image:21-07-290.jpg]] другого;<br>е) составляет 0,2 другого;<br>ж) составляет 60% другого;<br>з) составляет 140% другого». | + | [[Image:21-07-289.jpg|240px|Задание]]<br><br>1062. Составьте уравнение для решения задачи: «Поле площадью 2,4 га разделили на два участка. Найдите площадь каждого участка, если известно, что один из участков: |
| | + | |
| | + | а) на 0,8 га больше другого;<br>б) на 0,2 га меньше другого;<br>в) в 3 раза больше другого;<br>г) в 1,5 раза меньше другого;<br>д) составляет [[Image:21-07-290.jpg]] другого;<br>е) составляет 0,2 другого;<br>ж) составляет 60% другого;<br>з) составляет 140% другого». |
| | | | |
| | 1063. Решите задачу: | | 1063. Решите задачу: |
| Строка 85: |
Строка 108: |
| | '''Д''' 1065. Выполните сложение: | | '''Д''' 1065. Выполните сложение: |
| | | | |
| - | [[Image:21-07-291.jpg]]<br><br>1066. Представьте в виде суммы двух равных слагаемых кдое из чисел: [[Image:21-07-292.jpg]]<br>1067. Найдите значение а + b, если:<br>а) а= —1,6, b = 3,2; б) а=— 2,6, b = 1,9; в)[[Image:21-07-293.jpg]] | + | [[Image:21-07-291.jpg|480px|Задание]]<br><br>1066. Представьте в виде суммы двух равных слагаемых кдое из чисел: |
| | + | |
| | + | [[Image:21-07-292.jpg|320px|Задание]] |
| | + | |
| | + | <br>1067. Найдите значение а + b, если: |
| | + | |
| | + | а) а= —1,6, b = 3,2; б) а=— 2,6, b = 1,9; в)[[Image:21-07-293.jpg|Задание]] |
| | | | |
| | 1068. На одном этаже жилого дома было 8 квартир. 2 квартиры имели жилую площадь по 22,8 м<sup>2</sup>, 3 квартиры — по 16,2 м<sup>2</sup>, 2 квартиры — по 34 м<sup>2</sup>. Какую жилую площадь имела восьмая квартира, если на этом этаже в среднем на каждую квартиру приходилось по 24,7 м<sup>2</sup> жилой площади? | | 1068. На одном этаже жилого дома было 8 квартир. 2 квартиры имели жилую площадь по 22,8 м<sup>2</sup>, 3 квартиры — по 16,2 м<sup>2</sup>, 2 квартиры — по 34 м<sup>2</sup>. Какую жилую площадь имела восьмая квартира, если на этом этаже в среднем на каждую квартиру приходилось по 24,7 м<sup>2</sup> жилой площади? |
| Строка 91: |
Строка 120: |
| | 1069.В составе товарного поезда было 42 вагона. Крытых вагонов было в 1,2 раза больше, чем платформ, а число цистерн составляло [[Image:21-07-294.jpg]] числа платформ. Сколько вагонов каждого вида было в составе поезда? | | 1069.В составе товарного поезда было 42 вагона. Крытых вагонов было в 1,2 раза больше, чем платформ, а число цистерн составляло [[Image:21-07-294.jpg]] числа платформ. Сколько вагонов каждого вида было в составе поезда? |
| | | | |
| - | 1070. Найдите значение выражения[[Image:21-07-295.jpg]]<br><br><br><br><br> | + | 1070. Найдите значение выражения[[Image:21-07-295.jpg|Задание]]<br><br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> |
| | + | |
| | | | |
| - | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br>
| |
| | | | |
| | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 6 класса [[Математика|скачать]]</sub> | | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 6 класса [[Математика|скачать]]</sub> |
| Строка 100: |
Строка 129: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 16:20, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Сложение чисел с разными знаками
33. Сложение чисел с разными знаками
Если температура воздуха была равна 9 °С, а потом она изменилась на — 6 °С (т. е. понизилась на 6 °С), то она стала равной 9 + (— 6) градусам (рис. 83).
Чтобы сложить числа 9 и — 6 с помощью координатной прямой, надо точку А (9) переместить влево на 6 единичных отрезков (рис. 84). Получим точку В (3).

Значит, 9+( — 6) = 3. Число 3 имеет тот же знак, что и слагаемое 9, а его модуль равен разности модулей слагаемых 9 и —6.
Действительно, |3| =3 и |9| — |— 6| = = 9 — 6 = 3.
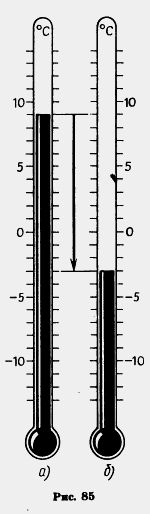
Если та же температура воздуха 9 °С изменилась на —12 °С (т. е. понизилась на 12 °С), то она стала равной 9 +( —12) градусам (рис. 85). Сложив числа 9 и —12 с помощью координатной прямой (рис. 86), получим 9 + ( —12)= —3. Число —3 имеет тот же знак, что и слагаемое —12, а его модуль равен разности модулей слагаемых —12 и 9.
Действительно, | — 3| = 3 и | —12| — | —9| =12 — 9 = 3.
Чтобы сложить два числа с разными знаками, надо:
1) из большего модуля слагаемых вычесть меньший;
2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
Обычно сначала определяют и записывают знак суммы, а потом находят разность модулей.

Например:
1) 6,1+(— 4,2)= +(6,1 — 4,2)= 1,9,
или короче 6,1+( — 4,2) = 6,1 — 4,2 = 1,9;
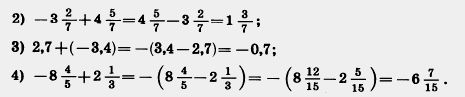
При сложении положительных и отрицательных чисел можно использовать микрокалькулятор. Чтобы ввести отрицательное число в микрокалькулятор, надо ввести модуль этого числа, потом нажать клавишу «изменение знака» |/—/|. Например, чтобы ввести число —56,81, надо последовательно нажимать клавиши: | 5 |, | 6 |, | ¦ |, | 8 |, | 1 |, |/—/|. Операции над числами любого знака выполняются на микрокалькуляторе так же, как над положительными числами.
Например, сумму —6,1 + 3,8 вычисляют по программе

? Числа а и b имеют разные знаки. Какой знак будет иметь сумма этих чисел, если больший модуль имеет отрицательное число?
если меньший модуль имеет отрицательное число?
если больший модуль имеет положительное число?
если меньший модуль имеет положительное число?
Сформулируйте правило сложения чисел с разными знаками. Как ввести в микрокалькулятор отрицательное число?
К 1045. Число 6 изменили на —10. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 6 и —10?
1046. Число 10 изменили на —6. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 10 и -6?
1047. Число —10 изменили на 3. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма —10 и 3?
1048. Число —10 изменили на 15. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма —10 и 15?
1049. В первую половину дня температура изменилась на — 4 °С, а во вторую — на + 12 °С. На сколько градусов изменилась температура в течение дня?
1050. Выполните сложение:
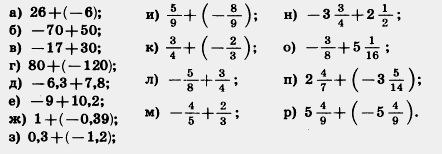
1051. Прибавьте:
а) к сумме —6 и —12 число 20;
б) к числу 2,6 сумму —1,8 и 5,2;
в) к сумме —10 и —1,3 сумму 5 и 8,7;
г) к сумме 11 и —6,5 сумму —3,2 и —6.
1052. Какое из чисел 8; 7,1; —7,1; —7; —0,5 является корнем уравнения — 6 + х =—13,1?
1053. Угадайте корень уравнения и выполните проверку:
а) х + ( —3)= —11; в) m + ( —12) = 2;
б) — 5 + y=15; г) 3 + n = —10.
1054. Найдите значение выражения:
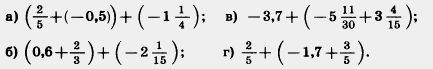
1055. Выполните действия с помощью микрокалькулятора:
а) — 3,2579 + ( —12,308); г) -3,8564+ (-0,8397) +7,84;
б) 7,8547+ ( — 9,239); д) -0,083 + (-6,378) + 3,9834;
в) —0,00154 + 0,0837; е) —0,0085+ 0,00354+ ( — 0,00921).
П 1056. Найдите значение суммы:
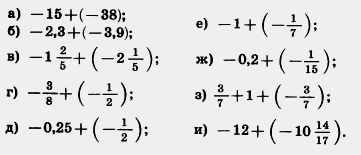
1057. Найдите значение выражения:
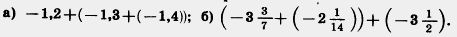
1058. Сколько целых чисел расположено между числами:
а) 0 и 24; б) —12 и —3; в) —20 и 7?
1059. Представьте число —10 в виде суммы двух отрицательных слагаемых так, чтобы:
а) оба слагаемых были целыми числами;
б) оба слагаемых были десятичными дробями;
в) одно из слагаемых было правильной обыкновенной дробью.
1060. Каково расстояние (в единичных отрезках) между точками координатной прямой с координатами:
а) 0 и а; б) —а и а; в) —а и 0; г) а и —За?
М 1061. Радиусы географических параллелей земной поверхности, на которых расположены города Афины и Москва, соответственно равны 5040 км и 3580 км (рис. 87). На сколько параллель Москвы короче параллели Афин?
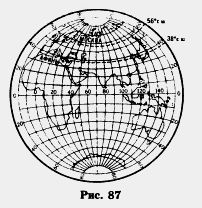
1062. Составьте уравнение для решения задачи: «Поле площадью 2,4 га разделили на два участка. Найдите площадь каждого участка, если известно, что один из участков:
а) на 0,8 га больше другого;
б) на 0,2 га меньше другого;
в) в 3 раза больше другого;
г) в 1,5 раза меньше другого;
д) составляет 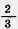 другого; другого;
е) составляет 0,2 другого;
ж) составляет 60% другого;
з) составляет 140% другого».
1063. Решите задачу:
1) В первый день путешественники проехали 240 км, во второй день 140 км, в третий день они проехали в 3 раза больше, чем во второй, а в четвертый день они отдыхали. Сколько километров они проехали в пятый день, если за 5 дней они проезжали в среднем по 230 км в день?
2) Заработок отца в месяц равен 280 р. Стипендия дочери в 4 раза меньше. Сколько зарабатывает в месяц мать, если в семье 4 человека, младший сын — школьник и на каждого приходится в среднем 135 р.?
1064. Выполните действия:
1) (2,35 + 4,65)• 5,3:(40—2,9);
2) (7,63—5,13)• 0,4:(3,17 + 6,83).
Д 1065. Выполните сложение:
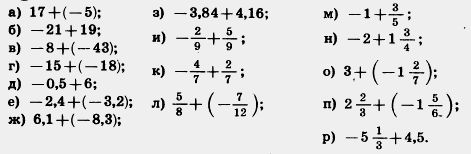
1066. Представьте в виде суммы двух равных слагаемых кдое из чисел:

1067. Найдите значение а + b, если:
а) а= —1,6, b = 3,2; б) а=— 2,6, b = 1,9; в)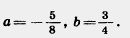
1068. На одном этаже жилого дома было 8 квартир. 2 квартиры имели жилую площадь по 22,8 м2, 3 квартиры — по 16,2 м2, 2 квартиры — по 34 м2. Какую жилую площадь имела восьмая квартира, если на этом этаже в среднем на каждую квартиру приходилось по 24,7 м2 жилой площади?
1069.В составе товарного поезда было 42 вагона. Крытых вагонов было в 1,2 раза больше, чем платформ, а число цистерн составляло 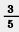 числа платформ. Сколько вагонов каждого вида было в составе поезда? числа платформ. Сколько вагонов каждого вида было в составе поезда?
1070. Найдите значение выражения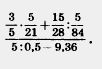
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Планирование по математике , учебники и книги онлайн, курсы и задачи по математике для 6 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|