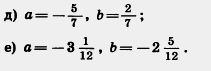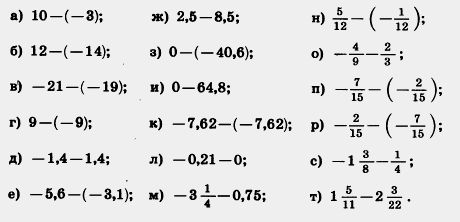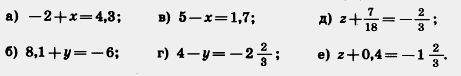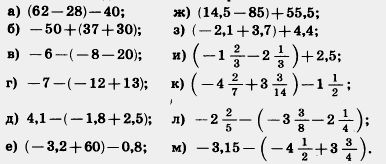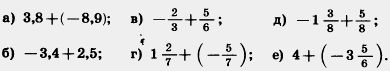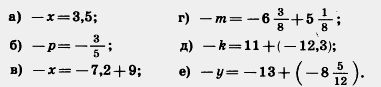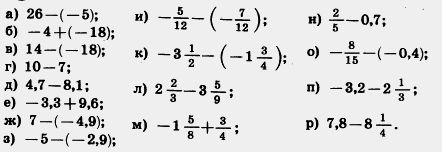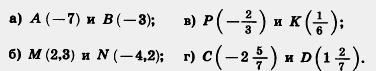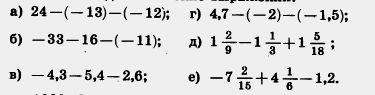|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' 34. Вычитание''' | + | '''34. Вычитание''' |
| | | | |
| | <br>Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому. | | <br>Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому. |
| Строка 11: |
Строка 11: |
| | Например, 8 + 3 = 11, и потому 11—8 = 3. Но 11 + ( —8) тоже равно 3. | | Например, 8 + 3 = 11, и потому 11—8 = 3. Но 11 + ( —8) тоже равно 3. |
| | | | |
| - | '''''Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому:'''''
| + | Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: |
| | | | |
| | а — b=а + ( — b). | | а — b=а + ( — b). |
| | | | |
| - | '''''Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.'''''
| + | Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как [http://xvatit.com/busines/ '''сумму''']. |
| | | | |
| | Например, —18 —14= —18 + ( —14); — 8 + 6 — k= — 8 + 6 + (-k). | | Например, —18 —14= —18 + ( —14); — 8 + 6 — k= — 8 + 6 + (-k). |
| Строка 23: |
Строка 23: |
| | Задача. Чему равна длина отрезка АВ, если А ( — 5) и В (9)? | | Задача. Чему равна длина отрезка АВ, если А ( — 5) и В (9)? |
| | | | |
| - | Решение. Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т. е. сколько надо прибавить к числу — 5, чтобы получилось число 9. Поэтому если обозначить длину отрезка АВ буквой х, то —5 + x = 9.<br>Отсюда х = 9 — ( — 5); x = 14. | + | Решение. Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т. е. сколько надо прибавить к числу — 5, чтобы получилось число 9. Поэтому если обозначить длину отрезка АВ буквой х, то —5 + x = 9. |
| | + | |
| | + | Отсюда х = 9 — ( — 5); x = 14. |
| | | | |
| | Значит, длина отрезка равна 14 единичным отрезкам. | | Значит, длина отрезка равна 14 единичным отрезкам. |
| | | | |
| - | '''''Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.'''''
| + | Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца. |
| | | | |
| - | '''? ''' Что означает вычитание отрицательных чисел? Каким действием можно заменить вычитание числа а из числа b? Ответ запишите в виде соответствующего буквенного равенства. Как найти длину отрезка на координатной прямой? | + | '''''? ''' Что означает вычитание отрицательных чисел? '' |
| | | | |
| - | 1071. За день температура воздуха изменилась на —12 °С и к вечеру стала равна — 8 °С. Какой была температура утром?
| + | ''Каким действием можно заменить вычитание числа а из числа b? '' |
| | | | |
| - | 1072. Температура воздуха утром была 5 °С, а к вечеру она стала равной — 2 °С. На сколько градусов изменилась температура воздуха за день?
| + | ''Ответ запишите в виде соответствующего буквенного равенства. Как найти длину отрезка на координатной прямой?'' |
| | | | |
| - | 1073. Вчера термометр показывал х °С, сегодня температура понизилась на 12 °С. Какую температуру показывает термометр сегодня, если х=25; 12; 6; 0?
| |
| | | | |
| - | Решите задачу двумя способами: сложением и вычитанием.
| |
| | | | |
| - | 1074. Проверьте равенство а — ( — b)=а+ b, если:
| + | 1071. За день температура воздуха изменилась на —12 °С и к вечеру стала равна — 8 °С. Какой была температура утром? |
| | | | |
| - | а) а =18, b = 16; г) а= — 4,8, b = 3,9;<br>б) а= —2,3, b= —0,5; <br>в) а = 44, b=-7; [[Image:21-07-296.jpg]]<br><br>''''' Г ''' Разность, в которую входят отрицательные числа, читают так:''
| + | 1072. Температура воздуха утром была 5 °С, а к вечеру она стала равной — 2 °С. На сколько градусов изменилась температура воздуха за день? |
| | | | |
| - | ''( — 7)—( — 12) — разность минус семи и минус двенадцати<br>— из минус семи вычесть минус двенадцать<br>— от минус семи отнять минус двенадцать''
| + | 1073. Вчера термометр показывал х °С, сегодня температура понизилась на 12 °С. Какую температуру показывает термометр сегодня, если х=25; 12; 6; 0? |
| | | | |
| - | <br>1075. Выполните вычитание:
| + | Решите задачу двумя способами: сложением и вычитанием. |
| | | | |
| - | [[Image:21-07-297.jpg]]<br><br>1076. Решите уравнение и выполните проверку:
| + | 1074. Проверьте равенство а — ( — b)=а+ b, если: |
| | | | |
| - | [[Image:21-07-298.jpg]]<br><br>1077. Представьте в виде суммы разность: | + | а) а =18, b = 16; г) а= — 4,8, b = 3,9;<br>б) а= —2,3, b= —0,5; <br>в) а = 44, b=-7; [[Image:21-07-296.jpg|Задание]]<br><br>''''' Г ''' Разность, в которую входят отрицательные числа, читают так:'' |
| | | | |
| - | а) — 28 —( — 32); в) 50-(-24); д) -30 —р;<br>б) —46 — 30; г) х —80; е) 6 —(—а).
| + | ''( — 7)—( — 12) — разность минус семи и минус двенадцати<br>— из минус семи вычесть минус двенадцать<br>— от минус семи отнять минус двенадцать'' |
| | | | |
| - | 1078. Назовите каждое слагаемое в сумме:
| + | <br>1075. Выполните вычитание: |
| | | | |
| - | а) — 8 + х; в) — m — 25; д) — n + 9 — k;<br>б) z — 6; г) 10 — a + y е) —а — b — с.
| + | [[Image:21-07-297.jpg|480px|Задание]]<br><br>1076. Решите уравнение и выполните проверку: |
| | | | |
| - | 1079. Составьте сумму из следующих слагаемых:
| + | [[Image:21-07-298.jpg|480px|Задание]]<br><br>1077. Представьте в виде суммы разность: |
| | | | |
| - | <br>а) -x; -у; -4,8; в) р; -20; 6; -к; 10,3;<br>б) 1,5; —а; b; — с; г) —7,6; m; — n; — t; —I.
| + | а) — 28 —( — 32); в) 50-(-24); д) -30 —р;<br>б) —46 — 30; г) х —80; е) 6 —(—а). |
| | | | |
| - | 1080. Найдите значение выражения:
| + | 1078. Назовите каждое слагаемое в сумме: |
| | | | |
| - | [[Image:21-07-299.jpg]]<br><br>1081. Найдите расстояние между точками А (a) и В (b), если: | + | а) — 8 + х; в) — m — 25; д) — n + 9 — k;<br>б) z — 6; г) 10 — a + y е) —а — b — с. |
| | + | |
| | + | 1079. Составьте сумму из следующих слагаемых: |
| | + | |
| | + | <br>а) -x; -у; -4,8; в) р; -20; 6; -к; 10,3;<br>б) 1,5; —а; b; — с; г) —7,6; m; — n; — t; —I. |
| | + | |
| | + | 1080. Найдите значение выражения: |
| | + | |
| | + | [[Image:21-07-299.jpg|420px|Задание]]<br><br>1081. Найдите расстояние между точками А (a) и В (b), если: |
| | | | |
| | а) а = 2, b = 8; в) a= — 1, b=6; д) а = 3,2, b=— 4,7;<br>б) a=—3, b= —5; г) а = 5, b=—4; е) а=—8,1, b=—2,5. | | а) а = 2, b = 8; в) a= — 1, b=6; д) а = 3,2, b=— 4,7;<br>б) a=—3, b= —5; г) а = 5, b=—4; е) а=—8,1, b=—2,5. |
| | | | |
| - | '''П ''' 1082. Выполните сложение: | + | '''П ''' 1082. Выполните сложение: |
| | | | |
| - | <br>[[Image:21-07-300.jpg]]<br><br>1083. Найдите значение выражения:<br>а) 3,75 + ( —2,11)+1,36; б) -4,27 + (-3,11)+(-0,62). | + | <br>[[Image:21-07-300.jpg|420px|Задание]]<br><br>1083. Найдите значение выражения:<br>а) 3,75 + ( —2,11)+1,36; б) -4,27 + (-3,11)+(-0,62). |
| | | | |
| - | 1084. Найдите число, противоположное [[Image:21-07-301.jpg]] ;3,85.<br>1085. Решите уравнение: | + | 1084. Найдите число, противоположное [[Image:21-07-301.jpg|Задание]] ;3,85.<br>1085. Решите уравнение: |
| | | | |
| - | [[Image:21-07-302.jpg]]<br><br>1086. Между какими соседними целыми числами располо жено число: [[Image:21-07-303.jpg]] | + | [[Image:21-07-302.jpg|420px|Задание]]<br><br>1086. Между какими соседними целыми числами расположено число: |
| | | | |
| - | 1087. Запишите все целые числа, модули которых: а) меньше 4; б) больше 4 и меньше 10. | + | [[Image:21-07-303.jpg|320px|Задание]] |
| | + | |
| | + | 1087. Запишите все целые числа, модули которых: а) меньше 4; б) больше 4 и меньше 10. |
| | | | |
| | 1088. Может ли сумма двух чисел быть меньше: | | 1088. Может ли сумма двух чисел быть меньше: |
| | | | |
| - | а) одного из слагаемых; б) каждого из слагаемых? | + | а) одного из слагаемых; б) каждого из слагаемых? |
| | | | |
| | Приведите примеры. | | Приведите примеры. |
| | | | |
| - | '''М''' 1089. Высота конуса 24 см, а площадь основания 15 см<sup>2</sup>. Какой высоты должен быть цилиндр с такой же площадью основания, чтобы его объем был равен объему конуса (рис. 88)? Нет ли в задаче лишних данных? | + | '''М''' 1089. Высота конуса 24 см, а площадь основания 15 см<sup>2</sup>. Какой высоты должен быть цилиндр с такой же площадью основания, чтобы его объем был равен объему конуса (рис. 88)? Нет ли в задаче лишних данных? |
| | | | |
| - | [[Image:21-07-304.jpg]]<br> <br>1090. На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свеклы, а капусты — на 80 кг больше, чем свеклы. Сколько килограммов каждой культуры было собрано? | + | [[Image:21-07-304.jpg|420px|Задание]]<br> <br>1090. На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свеклы, а капусты — на 80 кг больше, чем свеклы. Сколько килограммов каждой культуры было собрано? |
| | | | |
| - | 1091. Решите задачу:<br>1) В трех ящиках 21 кг гвоздей. В первом ящике в 1[[Image:21-07-305.jpg]] раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика<br>составляет [[Image:21-07-306.jpg]] массы гвоздей второго ящика. Сколько килограммов гвоздей было в каждом ящике? | + | 1091. Решите задачу:<br>1) В трех ящиках 21 кг гвоздей. В первом ящике в 1[[Image:21-07-305.jpg]] раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика<br>составляет [[Image:21-07-306.jpg]] массы гвоздей второго ящика. Сколько килограммов гвоздей было в каждом ящике? |
| | | | |
| - | 2) В овощеводческом совхозе помидоры, огурцы и морковь занимали 560 га. Посевы моркови составляли [[Image:21-07-307.jpg]] площади, занятой под огурцами, а под огурцами занято [[Image:21-07-308.jpg]] площади, отведенной под помидоры. Как велика площадь, занятая в отдельности помидорами, огурцами и морковью? | + | 2) В овощеводческом совхозе помидоры, огурцы и морковь занимали 560 га. Посевы моркови составляли [[Image:21-07-307.jpg]] площади, занятой под огурцами, а под огурцами занято [[Image:21-07-308.jpg]] площади, отведенной под помидоры. Как велика площадь, занятая в отдельности помидорами, огурцами и морковью? |
| | | | |
| - | 1092. Выполните действия: | + | 1092. Выполните действия: |
| | | | |
| | 1) 40,1 - 4,06• (29,58:3,48) + 8,112:0,78;<br>2) 50,2 —3,04• (45,22:4,76)+ 9,202:0,86. | | 1) 40,1 - 4,06• (29,58:3,48) + 8,112:0,78;<br>2) 50,2 —3,04• (45,22:4,76)+ 9,202:0,86. |
| | | | |
| - | '''Д '''1093. Выполните действие: | + | '''Д '''1093. Выполните действие: |
| | | | |
| - | [[Image:21-07-309.jpg]]<br><br>1094. Найдите значение выражения (а+b) — с, если: | + | [[Image:21-07-309.jpg|480px|Задание]]<br><br>1094. Найдите значение выражения (а+b) — с, если: |
| | | | |
| - | а) а = 2,6, b= —1,4, с = 2,1; б) а=b=—2,4, с=—3,9. | + | а) а = 2,6, b= —1,4, с = 2,1; б) а=b=—2,4, с=—3,9. |
| | | | |
| - | 1095. Отметьте на координатной прямой точки А (— 4) и В (9). Найдите расстояние между точками А и В в единичных отрезках. | + | 1095. Отметьте на координатной прямой точки А (— 4) и В (9). Найдите расстояние между точками А и В в единичных отрезках. |
| | | | |
| - | 1096. Найдите расстояние в единичных отрезках между точками: | + | 1096. Найдите расстояние в единичных отрезках между точками: |
| | | | |
| - | [[Image:21-07-310.jpg]] | + | [[Image:21-07-310.jpg|420px|Задание]] |
| | | | |
| - | <br>1097. Найдите значение выражения: | + | <br>1097. Найдите значение выражения: |
| | | | |
| - | [[Image:21-07-311.jpg]]<br><br>1098. Заполните пустые места таблицы: | + | [[Image:21-07-311.jpg|420px|Задание]]<br><br>1098. Заполните пустые места таблицы: |
| | | | |
| - | [[Image:21-07-312.jpg]]<br><br>1099. Для учащихся было куплено 70 билетов в кукольный театр. В партер было куплено билетов в 1,5 раза больше, чем на балкон и бельэтаж вместе. Число билетов на балкон составило 0,4 от числа билетов на бельэтаж. Сколько билетов каждого вида было куплено? | + | [[Image:21-07-312.jpg|480px|Задание]]<br><br>1099. Для учащихся было куплено 70 билетов в кукольный театр. В партер было куплено билетов в 1,5 раза больше, чем на балкон и бельэтаж вместе. Число билетов на балкон составило 0,4 от числа билетов на бельэтаж. Сколько билетов каждого вида было куплено? |
| | | | |
| - | 1100. В альбоме 1105 марок, число иностранных марок составило 30% от числа советских марок. Сколько иностранных и сколько советских марок было в альбоме? | + | 1100. В альбоме 1105 марок, число иностранных марок составило 30% от числа советских марок. Сколько иностранных и сколько советских марок было в альбоме? |
| | | | |
| - | 1101. В доме 300 квартир. Однокомнатные квартиры составляют 28% всех квартир дома, а остальные квартиры — двухкомнатные и трехкомнатные, причем двухкомнатных квартир в 1,7 раза больше, чем трехкомнатных. Сколько квартир каждого вида в доме? | + | 1101. В доме 300 квартир. Однокомнатные квартиры составляют 28% всех квартир дома, а остальные квартиры — двухкомнатные и трехкомнатные, причем двухкомнатных квартир в 1,7 раза больше, чем трехкомнатных. Сколько квартир каждого вида в доме? |
| | | | |
| - | ''' A ''' Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры. | + | ''' A ''' Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры. |
| | | | |
| - | Индийские математики представляли себе положительные числа как «имущества»,а отрицательные числа — как «долги». Вот как индийский математик Брахмагупта (VII в.) излагал правила сложения и вычитания: «Сумма двух имуществ есть имущество», «Сумма двух долгов есть долг», «Сумма имущества и долга равна их разности» и т. д. Попробуйте перевести эти древнеиндийские правила на современный язык.<br><br><br> | + | Индийские математики представляли себе положительные числа как «имущества»,а отрицательные числа — как «долги». Вот как индийский математик Брахмагупта (VII в.) излагал правила сложения и вычитания: «Сумма двух имуществ есть имущество», «Сумма двух долгов есть долг», «Сумма имущества и долга равна их разности» и т. д. Попробуйте перевести эти древнеиндийские правила на современный язык.<br> |
| | | | |
| | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> | | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> |
| | + | |
| | + | |
| | | | |
| | <sub>Учебники и книги по всему предметам, домашняя работа, [[Гипермаркет знаний - первый в мире!|онлайн]] библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 6 класса [[Математика|скачать]]</sub> | | <sub>Учебники и книги по всему предметам, домашняя работа, [[Гипермаркет знаний - первый в мире!|онлайн]] библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 6 класса [[Математика|скачать]]</sub> |
| Строка 128: |
Строка 140: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 16:23, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Вычитание-6 класс
34. Вычитание
Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому.
Например, 8 + 3 = 11, и потому 11—8 = 3. Но 11 + ( —8) тоже равно 3.
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому:
а — b=а + ( — b).
Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.
Например, —18 —14= —18 + ( —14); — 8 + 6 — k= — 8 + 6 + (-k).
Разность двух чисел положительна, если уменьшаемое больше вычитаемого, и отрицательна, если уменьшаемое меньше вычитаемого. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.
Задача. Чему равна длина отрезка АВ, если А ( — 5) и В (9)?
Решение. Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т. е. сколько надо прибавить к числу — 5, чтобы получилось число 9. Поэтому если обозначить длину отрезка АВ буквой х, то —5 + x = 9.
Отсюда х = 9 — ( — 5); x = 14.
Значит, длина отрезка равна 14 единичным отрезкам.
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
? Что означает вычитание отрицательных чисел?
Каким действием можно заменить вычитание числа а из числа b?
Ответ запишите в виде соответствующего буквенного равенства. Как найти длину отрезка на координатной прямой?
1071. За день температура воздуха изменилась на —12 °С и к вечеру стала равна — 8 °С. Какой была температура утром?
1072. Температура воздуха утром была 5 °С, а к вечеру она стала равной — 2 °С. На сколько градусов изменилась температура воздуха за день?
1073. Вчера термометр показывал х °С, сегодня температура понизилась на 12 °С. Какую температуру показывает термометр сегодня, если х=25; 12; 6; 0?
Решите задачу двумя способами: сложением и вычитанием.
1074. Проверьте равенство а — ( — b)=а+ b, если:
а) а =18, b = 16; г) а= — 4,8, b = 3,9;
б) а= —2,3, b= —0,5;
в) а = 44, b=-7; 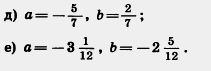
Г Разность, в которую входят отрицательные числа, читают так:
( — 7)—( — 12) — разность минус семи и минус двенадцати
— из минус семи вычесть минус двенадцать
— от минус семи отнять минус двенадцать
1075. Выполните вычитание:
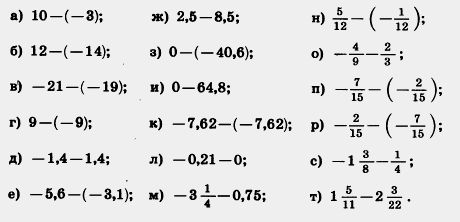
1076. Решите уравнение и выполните проверку:
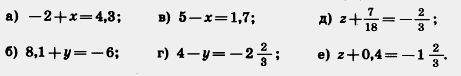
1077. Представьте в виде суммы разность:
а) — 28 —( — 32); в) 50-(-24); д) -30 —р;
б) —46 — 30; г) х —80; е) 6 —(—а).
1078. Назовите каждое слагаемое в сумме:
а) — 8 + х; в) — m — 25; д) — n + 9 — k;
б) z — 6; г) 10 — a + y е) —а — b — с.
1079. Составьте сумму из следующих слагаемых:
а) -x; -у; -4,8; в) р; -20; 6; -к; 10,3;
б) 1,5; —а; b; — с; г) —7,6; m; — n; — t; —I.
1080. Найдите значение выражения:
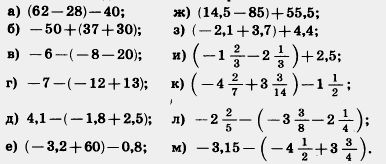
1081. Найдите расстояние между точками А (a) и В (b), если:
а) а = 2, b = 8; в) a= — 1, b=6; д) а = 3,2, b=— 4,7;
б) a=—3, b= —5; г) а = 5, b=—4; е) а=—8,1, b=—2,5.
П 1082. Выполните сложение:
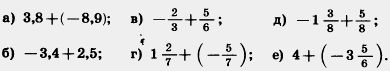
1083. Найдите значение выражения:
а) 3,75 + ( —2,11)+1,36; б) -4,27 + (-3,11)+(-0,62).
1084. Найдите число, противоположное 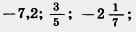 ;3,85. ;3,85.
1085. Решите уравнение:
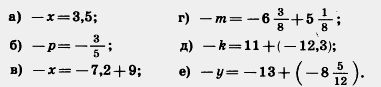
1086. Между какими соседними целыми числами расположено число:
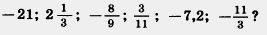
1087. Запишите все целые числа, модули которых: а) меньше 4; б) больше 4 и меньше 10.
1088. Может ли сумма двух чисел быть меньше:
а) одного из слагаемых; б) каждого из слагаемых?
Приведите примеры.
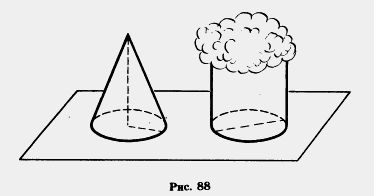
М 1089. Высота конуса 24 см, а площадь основания 15 см2. Какой высоты должен быть цилиндр с такой же площадью основания, чтобы его объем был равен объему конуса (рис. 88)? Нет ли в задаче лишних данных?
1090. На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свеклы, а капусты — на 80 кг больше, чем свеклы. Сколько килограммов каждой культуры было собрано?
1091. Решите задачу:
1) В трех ящиках 21 кг гвоздей. В первом ящике в 1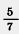 раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика
составляет 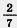 массы гвоздей второго ящика. Сколько килограммов гвоздей было в каждом ящике? массы гвоздей второго ящика. Сколько килограммов гвоздей было в каждом ящике?
2) В овощеводческом совхозе помидоры, огурцы и морковь занимали 560 га. Посевы моркови составляли 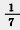 площади, занятой под огурцами, а под огурцами занято площади, занятой под огурцами, а под огурцами занято 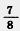 площади, отведенной под помидоры. Как велика площадь, занятая в отдельности помидорами, огурцами и морковью? площади, отведенной под помидоры. Как велика площадь, занятая в отдельности помидорами, огурцами и морковью?
1092. Выполните действия:
1) 40,1 - 4,06• (29,58:3,48) + 8,112:0,78;
2) 50,2 —3,04• (45,22:4,76)+ 9,202:0,86.
Д 1093. Выполните действие:
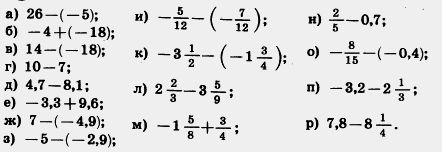
1094. Найдите значение выражения (а+b) — с, если:
а) а = 2,6, b= —1,4, с = 2,1; б) а=b=—2,4, с=—3,9.
1095. Отметьте на координатной прямой точки А (— 4) и В (9). Найдите расстояние между точками А и В в единичных отрезках.
1096. Найдите расстояние в единичных отрезках между точками:
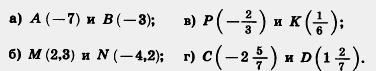
1097. Найдите значение выражения:
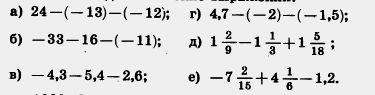
1098. Заполните пустые места таблицы:
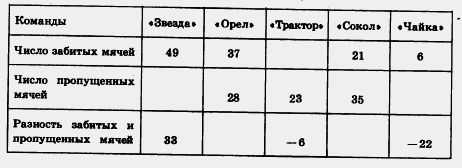
1099. Для учащихся было куплено 70 билетов в кукольный театр. В партер было куплено билетов в 1,5 раза больше, чем на балкон и бельэтаж вместе. Число билетов на балкон составило 0,4 от числа билетов на бельэтаж. Сколько билетов каждого вида было куплено?
1100. В альбоме 1105 марок, число иностранных марок составило 30% от числа советских марок. Сколько иностранных и сколько советских марок было в альбоме?
1101. В доме 300 квартир. Однокомнатные квартиры составляют 28% всех квартир дома, а остальные квартиры — двухкомнатные и трехкомнатные, причем двухкомнатных квартир в 1,7 раза больше, чем трехкомнатных. Сколько квартир каждого вида в доме?
A Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры.
Индийские математики представляли себе положительные числа как «имущества»,а отрицательные числа — как «долги». Вот как индийский математик Брахмагупта (VII в.) излагал правила сложения и вычитания: «Сумма двух имуществ есть имущество», «Сумма двух долгов есть долг», «Сумма имущества и долга равна их разности» и т. д. Попробуйте перевести эти древнеиндийские правила на современный язык.
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 6 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|