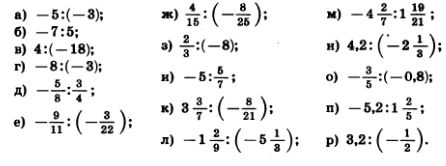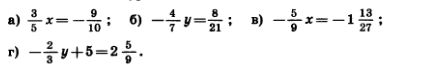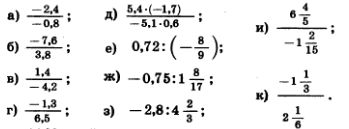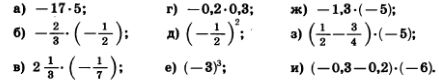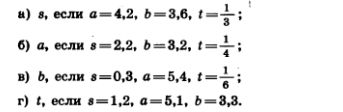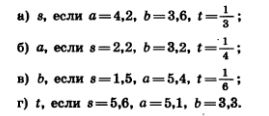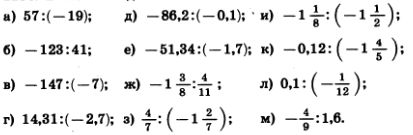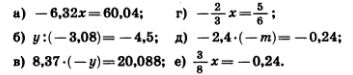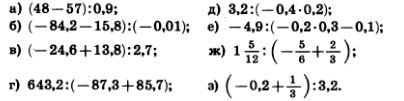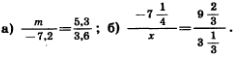|
|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Деление''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Деление''' |
| | | | |
| - | <br>
| |
| | | | |
| - | '''36. Деление'''<br>Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель.<br>
| + | '''36. Деление''' |
| | | | |
| - | Например, разделить —12 на — 4 — это значит найти такое число х, что — 4x= —12. Сначала найдем знак числа х. Так как при умножении — 4 на х получилось отрицательное число —12, то множители —4 и х должны иметь разные знаки. Поэтому х — положительное число. Теперь найдем модуль числа х. Так как модуль произведения равен произведению модулей множителей, то | —12| = | —4| • |x|. Отсюда |x| = | —12|: I —4|. Но так как х — положительное число, то х=|х|. Значит, х = 3.<br>Пишут: ( —12):( — 4)= |—12|: |—4|=3, или короче: ( — 12):( —4)=12:4 = 3.<br>
| |
| | | | |
| - | '''''Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.'''''<br>
| |
| | | | |
| - | Например, —4,5: ( — 1,5)=4,5:1,5 = 3;<br>[[Image:2010-174.jpg]]<br>Разделить — 24 на 4 — это значит найти такое число х, что 4 • х= —24. При умножении 4 на х получилось отрицательное число —24, значит, множители 4 и х должны иметь разные знаки. Поэтому х — отрицательное число. При этом должно выполняться равенство |4|•|x|=|—24|. Отсюда I х | = | — 24|:|4| = 24:4 = 6. Значит, х — отрицательное число с модулем 6, т. е. х = — 6.<br>Итак, —24:4=—6.<br>Рассуждая таким же образом, получим, что 24:( —4)= — 6.<br>
| + | Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель.<br> |
| | | | |
| - | '''''При делении чисел с разными знаками, надо: 1) разделить модуль делимого на модуль делителя; 2) поставить перед полученным числом знак «—».'''''<br>
| + | Например, разделить —12 на — 4 — это значит найти такое число х, что — 4x= —12. Сначала найдем знак числа х. Так как при умножении — 4 на х получилось отрицательное число —12, то множители —4 и х должны иметь разные знаки. Поэтому х — положительное число. Теперь найдем модуль числа х. Так как модуль произведения равен произведению модулей множителей, то | —12| = | —4| • |x|. Отсюда |x| = | —12|: I —4|. Но так как х — положительное число, то х=|х|. Значит, х = 3. |
| | | | |
| - | ''Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.''<br>Например, 3,6:(— 3) = — (3,6:3) = —1,2;<br>[[Image:2010-175.jpg]]<br>''При делении нуля на любое число, не равное нулю, получается нуль. '''''<i>Делить на нуль нельзя!</i>'''<br>7 Зак. 607 <br>[[Image:2010-09.jpg]]Сформулируйте правило деления отрицательного числа на отрицательное. Сформулируйте правило, деления чисел, имеющих разные знаки. Чему равно частное 0:а, где а[[Image:2010-80.jpg]]О?<br>[[Image:2010-09k.jpg]]1133. Верно ли выполнено деление:<br>а) -36:2=-18; в) 2,7:(-1)=2,7;<br>б) 60:( —1,5)= —4; г) -7,5:(-5)=1,5?<br>
| + | Пишут: ( —12):( — 4)= |—12|: |—4|=3, или короче: ( — 12):( —4)=12:4 = 3.<br> |
| | | | |
| - | 1134. Найдите частное:<br>а) -38:19; д) — 6,1:(—17); и) 48,1 :(-48,1);<br>б) 45:( —15); е) 650:(-1,3); к) -950:9,5;<br>в) —36:( — 6); ж) -4,4:4; л) -5,42:(-27,1);<br>г) 270:( — 9); з) -8,6:( —4,3); м) 10,01:(-1,3).<br>[[Image:2010-09g.jpg]]Частное, в которое входят отрицательные числа, читают так:<br>-54:(— 2,7) — частное минус пятидесяти четырех и минус двух целых семи десятых<br>— минус пятьдесят четыре разделить на минус две целых семь десятых<br>(— 6m):( — 3) — частное минус шести эм и минус трех<br>— минус шесть эм разделить на минус три Равенство, содержащее отрицательные числа, читают так:<br>[[Image:2010-176.jpg]] минус две седьмых икс равны минус четырем одиннадцатым<br>
| + | '''''Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.'''''<br> |
| | | | |
| - | 1135. Выполните деление: <br>[[Image:2010-177.jpg]]<br>1136. Выполните действия:<br>а) — 4•( — 6)—( — 30):6; д) (-8 + 32):(-6)-7;<br>б) 15:( —15)—( —24):8; е) -21+(-3-4 + 5):(-2);<br>в) -8(-3 + 12):36 + 2; ж) -6•4-64:(-3,3 + 1,7);<br>г) 2,3•(—6 —4):5; з) (-6+6,4-10):(-8)•(-3).
| + | Например, —4,5: ( — 1,5)=4,5:1,5 = 3; [[Image:2010-174.jpg|Задание]] |
| | | | |
| - | 1137. Найдите значение выражения:<br>а) (3m + 6m):9, если m= —12; —5,96;<br>б) (5,2а— 5,2b):5,2, если а=—27, b=— 3,64.
| + | Разделить — 24 на 4 — это значит найти такое число х, что 4 • х= —24. При умножении 4 на х получилось отрицательное число —24, значит, множители 4 и х должны иметь разные знаки. Поэтому х — отрицательное число. При этом должно выполняться равенство |4|•|x|=|—24|. Отсюда I х | = | — 24|:|4| = 24:4 = 6. Значит, х — отрицательное число с модулем 6, т. е. х = — 6. |
| | | | |
| - | 1138. Чему равно частное:<br>а) 87x и 87; г) —41с и с;<br>б) — 3,7k и 3,7; д) —1,9x и х?<br>в) 9m и m
| + | Итак, —24:4=—6. |
| | | | |
| - | 1139. Решите уравнение и выполните проверку:<br>[[Image:2010-178.jpg]]<br>1140. Решите уравнение:<br>[[Image:2010-179.jpg]]<br>1141. Я задумал число, умножил его на 5, а затем из произведения вычел 2,7. В результате получил —21,7. Какое число я задумал?<br>1142. Найдите значение выражения: <br>[[Image:2010-180.jpg]]<br>1143. Найдите неизвестный член пропорции:<br>[[Image:2010-181.jpg]]<br>[[Image:2010-09p.jpg]]1144. Вычислите устно: <br>[[Image:2010-182.jpg]]<br>1145. При каких значениях множителей произведение ху равно нулю? не равно нулю?
| + | Рассуждая таким же образом, получим, что 24:( —4)= — 6.<br> |
| | | | |
| - | 1146. В каких случаях может быть верно равенство: а) х = х <sup>2</sup>; б) х = х<sup>3</sup> ; в) х<sup>2</sup> = х<sup>3</sup>?
| + | '''''При делении чисел с разными знаками, надо: 1) разделить модуль делимого на модуль делителя; 2) поставить перед полученным числом знак «—».'''''<br> |
| | | | |
| - | 1147. Проверьте на примерах справедливость равенства |аb| = |a| • |b|. Попробуйте доказать, что это равенство верно при любых значениях а и b.
| + | Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.<br>Например, 3,6:(— 3) = — (3,6:3) = —1,2; [[Image:2010-175.jpg|320px|Задание]]<br>При делении нуля на любое число, не равное нулю, получается нуль. Делить на нуль нельзя!<br><br>[[Image:2010-09.jpg]]Сформулируйте правило деления отрицательного числа на отрицательное. Сформулируйте правило, деления чисел, имеющих разные знаки. Чему равно частное 0:а, где а[[Image:2010-80.jpg]]О?<br>[[Image:2010-09k.jpg]]1133. Верно ли выполнено деление:<br>а) -36:2=-18; в) 2,7:(-1)=2,7;<br>б) 60:( —1,5)= —4; г) -7,5:(-5)=1,5?<br> |
| | | | |
| - | 1148. Вычислите:<br>[[Image:2010-183.jpg]]<br>1149. Представьте числа 9; 16 и 25 в виде произведения двух равных множителей. Сколькими способами можно это сделать?<br>1150. Найдите значение выражения:<br>а) - 2,3 • 0,1 + 35 • (- 0,01) - (- 2,1) • (- 0,2);<br>б) (4,8 — 7,3 + 2,1 — 2,7 + 3,1) • (—183).
| |
| | | | |
| - | [[Image:2010-09m.jpg]]1151. На рисунке 90 показана карта мира с часовыми поясами. Определите с ее помощью: а) поясное время в Свердловске и во Владивостоке, если в Москве полночь; б) поясное время в Лондоне, Токио, Нью-Йорке и Дели, если в Москве 11ч утра. Составьте сами и решите несколько задач на определение поясного времени.<br> [[Image:2010-184.jpg]]<br>1152. Костя и Вера вышли одновременно из одного и того же пункта в одном и том же направлении. Костя идет со скоростью а км/ч, а Вера — со скоростью b км/ч. Какое расстояние будет между ними через t ч? Составьте формулу для решения задачи, обозначив испокомое расстояние (в километрах) буквой s и зная что a>b. Найдите по формуле:<br>[[Image:2010-185.jpg]]<br>1153. Решите предыдущую задачу, заменив в ней слова «в одном и том же направлении» на слова «в противоположных направлениях». Найдите по полученной формуле:<br>[[Image:2010-186.jpg]]<br>1154. При каких целых значениях х верно неравенство:
| |
| | | | |
| - | [[Image:2010-187.jpg]]<br>1155. Вычислите с помощью микрокалькулятора: а) -3,82• 0,375-3,8275; б) 4,15• (-1,236)+3,0994.
| + | 1134. Найдите частное: |
| | | | |
| - | [[Image:2010-09d.jpg]]1156. Выполните деление:<br>[[Image:2010-188.jpg]]<br>1157. Решите уравнение:<br>[[Image:2010-189.jpg]]<br>1158. Найдите значение выражения:<br>[[Image:2010-190.jpg]]<br>1159. Из города одновременно в одном и том же направлении выехали два мотоциклиста. Скорость первого из них была больше скорости второго и составляла 72 км/ч. Через 25 мин расстояние между мотоциклистами было равно 5 км. Найдите скорость второго мотоциклиста.<br>1160. Найдите значение выражения | + | а) -38:19; д) — 6,1:(—17); и) 48,1 :(-48,1);<br>б) 45:( —15); е) 650:(-1,3); к) -950:9,5;<br>в) —36:( — 6); ж) -4,4:4; л) -5,42:(-27,1);<br>г) 270:( — 9); з) -8,6:( —4,3); м) 10,01:(-1,3). |
| | + | |
| | + | <br>[[Image:2010-09g.jpg]]Частное, в которое входят отрицательные числа, читают так:<br>-54:(— 2,7) — частное минус пятидесяти четырех и минус двух целых семи десятых — минус пятьдесят четыре разделить на минус две целых семь десятых (— 6m):( — 3) — частное минус шести эм и минус трех<br>— минус шесть эм разделить на минус три Равенство, содержащее отрицательные числа, читают так:<br>[[Image:2010-176.jpg|Задание]] минус две седьмых икс равны минус четырем одиннадцатым<br> |
| | + | |
| | + | 1135. Выполните деление: |
| | + | |
| | + | [[Image:2010-177.jpg|480px|Задание]]<br>1136. Выполните действия: |
| | + | |
| | + | а) — 4•( — 6)—( — 30):6; д) (-8 + 32):(-6)-7;<br>б) 15:( —15)—( —24):8; е) -21+(-3-4 + 5):(-2);<br>в) -8(-3 + 12):36 + 2; ж) -6•4-64:(-3,3 + 1,7);<br>г) 2,3•(—6 —4):5; з) (-6+6,4-10):(-8)•(-3). |
| | + | |
| | + | 1137. Найдите значение выражения: |
| | + | |
| | + | а) (3m + 6m):9, если m= —12; —5,96;<br>б) (5,2а— 5,2b):5,2, если а=—27, b=— 3,64. |
| | + | |
| | + | 1138. Чему равно частное: |
| | + | |
| | + | а) 87x и 87; г) —41с и с;<br>б) — 3,7k и 3,7; д) —1,9x и х?<br>в) 9m и m |
| | + | |
| | + | 1139. Решите уравнение и выполните проверку:<br>[[Image:2010-178.jpg|420px|Задание]] |
| | + | |
| | + | <br>1140. Решите уравнение: |
| | + | |
| | + | [[Image:2010-179.jpg|420px|Задание]] |
| | + | |
| | + | <br>1141. Я задумал число, умножил его на 5, а затем из произведения вычел 2,7. В результате получил —21,7. Какое число я задумал? |
| | + | |
| | + | 1142. Найдите значение выражения: |
| | + | |
| | + | [[Image:2010-180.jpg|320px|Задание]] |
| | + | |
| | + | <br>1143. Найдите неизвестный член пропорции: |
| | + | |
| | + | [[Image:2010-181.jpg|420px|Задание]]<br>[[Image:2010-09p.jpg]]1144. Вычислите устно: <br>[[Image:2010-182.jpg|480px|Задание]] |
| | + | |
| | + | <br>1145. При каких значениях множителей произведение ху равно нулю? не равно нулю? |
| | + | |
| | + | 1146. В каких случаях может быть верно равенство: а) х = х <sup>2</sup>; б) х = х<sup>3</sup> ; в) х<sup>2</sup> = х<sup>3</sup>? |
| | + | |
| | + | 1147. Проверьте на примерах справедливость равенства |аb| = |a| • |b|. Попробуйте доказать, что это равенство верно при любых значениях а и b. |
| | + | |
| | + | 1148. Вычислите: |
| | + | |
| | + | [[Image:2010-183.jpg|480px|Задание]] |
| | + | |
| | + | <br>1149. Представьте числа 9; 16 и 25 в виде произведения двух равных множителей. Сколькими способами можно это сделать? |
| | + | |
| | + | 1150. Найдите значение выражения: |
| | + | |
| | + | а) - 2,3 • 0,1 + 35 • (- 0,01) - (- 2,1) • (- 0,2);<br>б) (4,8 — 7,3 + 2,1 — 2,7 + 3,1) • (—183). |
| | + | |
| | + | [[Image:2010-09m.jpg]]1151. На рисунке 90 показана карта мира с часовыми поясами. Определите с ее помощью: а) поясное время в Свердловске и во Владивостоке, если в Москве полночь; б) поясное время в Лондоне, Токио, Нью-Йорке и Дели, если в Москве 11ч утра. Составьте сами и решите несколько задач на определение поясного времени.<br> [[Image:2010-184.jpg|480px|Задание]]<br>1152. Костя и Вера вышли одновременно из одного и того же пункта в одном и том же направлении. Костя идет со скоростью а км/ч, а Вера — со скоростью b км/ч. Какое расстояние будет между ними через t ч? Составьте формулу для решения задачи, обозначив испокомое расстояние (в километрах) буквой s и зная что a>b. Найдите по формуле: |
| | + | |
| | + | <br>[[Image:2010-185.jpg|320px|Задание]] |
| | + | |
| | + | <br>1153. Решите предыдущую задачу, заменив в ней слова «в одном и том же направлении» на слова «в противоположных направлениях». Найдите по полученной формуле: |
| | + | |
| | + | <br>[[Image:2010-186.jpg|320px|Задание]] |
| | + | |
| | + | <br>1154. При каких целых значениях х верно неравенство: |
| | + | |
| | + | [[Image:2010-187.jpg|480px|Задание]] |
| | + | |
| | + | <br>1155. Вычислите с помощью микрокалькулятора: а) -3,82• 0,375-3,8275; б) 4,15• (-1,236)+3,0994. |
| | + | |
| | + | [[Image:2010-09d.jpg]]1156. Выполните деление:<br>[[Image:2010-188.jpg|480px|Задание]] |
| | + | |
| | + | <br>1157. Решите уравнение: |
| | + | |
| | + | [[Image:2010-189.jpg|320px|Задание]] |
| | + | |
| | + | <br>1158. Найдите значение выражения: |
| | + | |
| | + | [[Image:2010-190.jpg|480px|Задание]]<br>1159. Из города одновременно в одном и том же направлении выехали два мотоциклиста. Скорость первого из них была больше скорости второго и составляла 72 км/ч. Через 25 мин расстояние между мотоциклистами было равно 5 км. Найдите скорость второго мотоциклиста. |
| | + | |
| | + | <br>1160. Найдите значение выражения |
| | + | |
| | + | [[Image:2010-191.jpg|Задание]] |
| | + | |
| | + | <br>1161. Решите уравнение |
| | + | |
| | + | <br>[[Image:2010-192.jpg|240px|Задание]] <br> |
| | + | |
| | + | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, [http://xvatit.com/vuzi/ '''Математика'''] для 6 класса, Учебник для средней школы'' <br> |
| | | | |
| - | [[Image:2010-191.jpg]]<br>1161. Решите уравнение<br>[[Image:2010-192.jpg]] <br>
| |
| | | | |
| - | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br>
| |
| | | | |
| | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 6 класса [[Математика|скачать]]</sub> | | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 6 класса [[Математика|скачать]]</sub> |
| Строка 48: |
Строка 123: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 16:34, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Деление
36. Деление
Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель.
Например, разделить —12 на — 4 — это значит найти такое число х, что — 4x= —12. Сначала найдем знак числа х. Так как при умножении — 4 на х получилось отрицательное число —12, то множители —4 и х должны иметь разные знаки. Поэтому х — положительное число. Теперь найдем модуль числа х. Так как модуль произведения равен произведению модулей множителей, то | —12| = | —4| • |x|. Отсюда |x| = | —12|: I —4|. Но так как х — положительное число, то х=|х|. Значит, х = 3.
Пишут: ( —12):( — 4)= |—12|: |—4|=3, или короче: ( — 12):( —4)=12:4 = 3.
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
Например, —4,5: ( — 1,5)=4,5:1,5 = 3; 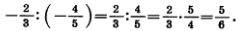
Разделить — 24 на 4 — это значит найти такое число х, что 4 • х= —24. При умножении 4 на х получилось отрицательное число —24, значит, множители 4 и х должны иметь разные знаки. Поэтому х — отрицательное число. При этом должно выполняться равенство |4|•|x|=|—24|. Отсюда I х | = | — 24|:|4| = 24:4 = 6. Значит, х — отрицательное число с модулем 6, т. е. х = — 6.
Итак, —24:4=—6.
Рассуждая таким же образом, получим, что 24:( —4)= — 6.
При делении чисел с разными знаками, надо: 1) разделить модуль делимого на модуль делителя; 2) поставить перед полученным числом знак «—».
Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.
Например, 3,6:(— 3) = — (3,6:3) = —1,2; 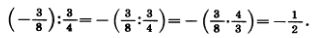
При делении нуля на любое число, не равное нулю, получается нуль. Делить на нуль нельзя!
 Сформулируйте правило деления отрицательного числа на отрицательное. Сформулируйте правило, деления чисел, имеющих разные знаки. Чему равно частное 0:а, где а Сформулируйте правило деления отрицательного числа на отрицательное. Сформулируйте правило, деления чисел, имеющих разные знаки. Чему равно частное 0:а, где а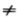 О? О?
 1133. Верно ли выполнено деление: 1133. Верно ли выполнено деление:
а) -36:2=-18; в) 2,7:(-1)=2,7;
б) 60:( —1,5)= —4; г) -7,5:(-5)=1,5?
1134. Найдите частное:
а) -38:19; д) — 6,1:(—17); и) 48,1 :(-48,1);
б) 45:( —15); е) 650:(-1,3); к) -950:9,5;
в) —36:( — 6); ж) -4,4:4; л) -5,42:(-27,1);
г) 270:( — 9); з) -8,6:( —4,3); м) 10,01:(-1,3).
 Частное, в которое входят отрицательные числа, читают так: Частное, в которое входят отрицательные числа, читают так:
-54:(— 2,7) — частное минус пятидесяти четырех и минус двух целых семи десятых — минус пятьдесят четыре разделить на минус две целых семь десятых (— 6m):( — 3) — частное минус шести эм и минус трех
— минус шесть эм разделить на минус три Равенство, содержащее отрицательные числа, читают так:
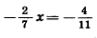 минус две седьмых икс равны минус четырем одиннадцатым минус две седьмых икс равны минус четырем одиннадцатым
1135. Выполните деление:
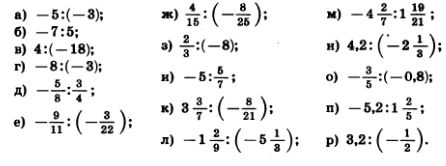
1136. Выполните действия:
а) — 4•( — 6)—( — 30):6; д) (-8 + 32):(-6)-7;
б) 15:( —15)—( —24):8; е) -21+(-3-4 + 5):(-2);
в) -8(-3 + 12):36 + 2; ж) -6•4-64:(-3,3 + 1,7);
г) 2,3•(—6 —4):5; з) (-6+6,4-10):(-8)•(-3).
1137. Найдите значение выражения:
а) (3m + 6m):9, если m= —12; —5,96;
б) (5,2а— 5,2b):5,2, если а=—27, b=— 3,64.
1138. Чему равно частное:
а) 87x и 87; г) —41с и с;
б) — 3,7k и 3,7; д) —1,9x и х?
в) 9m и m
1139. Решите уравнение и выполните проверку:
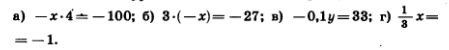
1140. Решите уравнение:
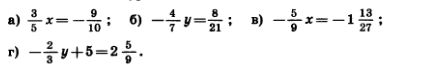
1141. Я задумал число, умножил его на 5, а затем из произведения вычел 2,7. В результате получил —21,7. Какое число я задумал?
1142. Найдите значение выражения:
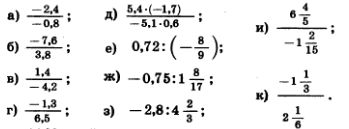
1143. Найдите неизвестный член пропорции:
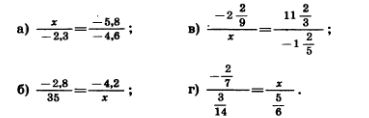
 1144. Вычислите устно: 1144. Вычислите устно:
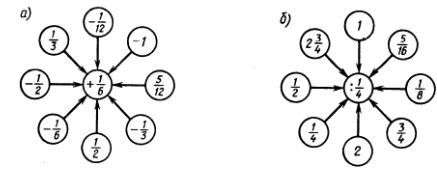
1145. При каких значениях множителей произведение ху равно нулю? не равно нулю?
1146. В каких случаях может быть верно равенство: а) х = х 2; б) х = х3 ; в) х2 = х3?
1147. Проверьте на примерах справедливость равенства |аb| = |a| • |b|. Попробуйте доказать, что это равенство верно при любых значениях а и b.
1148. Вычислите:
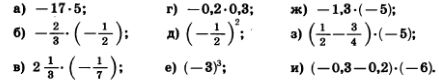
1149. Представьте числа 9; 16 и 25 в виде произведения двух равных множителей. Сколькими способами можно это сделать?
1150. Найдите значение выражения:
а) - 2,3 • 0,1 + 35 • (- 0,01) - (- 2,1) • (- 0,2);
б) (4,8 — 7,3 + 2,1 — 2,7 + 3,1) • (—183).
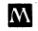 1151. На рисунке 90 показана карта мира с часовыми поясами. Определите с ее помощью: а) поясное время в Свердловске и во Владивостоке, если в Москве полночь; б) поясное время в Лондоне, Токио, Нью-Йорке и Дели, если в Москве 11ч утра. Составьте сами и решите несколько задач на определение поясного времени. 1151. На рисунке 90 показана карта мира с часовыми поясами. Определите с ее помощью: а) поясное время в Свердловске и во Владивостоке, если в Москве полночь; б) поясное время в Лондоне, Токио, Нью-Йорке и Дели, если в Москве 11ч утра. Составьте сами и решите несколько задач на определение поясного времени.
1152. Костя и Вера вышли одновременно из одного и того же пункта в одном и том же направлении. Костя идет со скоростью а км/ч, а Вера — со скоростью b км/ч. Какое расстояние будет между ними через t ч? Составьте формулу для решения задачи, обозначив испокомое расстояние (в километрах) буквой s и зная что a>b. Найдите по формуле:
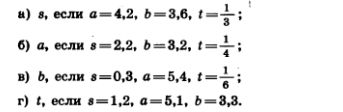
1153. Решите предыдущую задачу, заменив в ней слова «в одном и том же направлении» на слова «в противоположных направлениях». Найдите по полученной формуле:
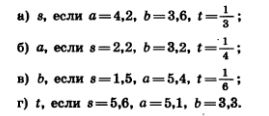
1154. При каких целых значениях х верно неравенство:
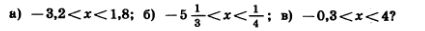
1155. Вычислите с помощью микрокалькулятора: а) -3,82• 0,375-3,8275; б) 4,15• (-1,236)+3,0994.
 1156. Выполните деление: 1156. Выполните деление:
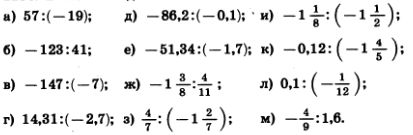
1157. Решите уравнение:
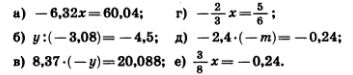
1158. Найдите значение выражения:
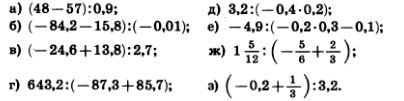
1159. Из города одновременно в одном и том же направлении выехали два мотоциклиста. Скорость первого из них была больше скорости второго и составляла 72 км/ч. Через 25 мин расстояние между мотоциклистами было равно 5 км. Найдите скорость второго мотоциклиста.
1160. Найдите значение выражения
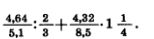
1161. Решите уравнение
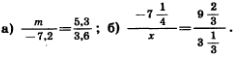
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 6 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|