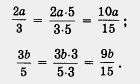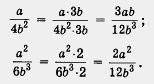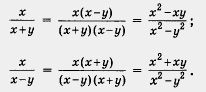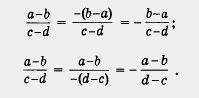|
|
| (3 промежуточные версии не показаны) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Основное свойство алгебраической дроби </metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Основное свойство алгебраической дроби, обыкновенной дроби, знаменатель, сокращением, алгебраической дроби, преобразование</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Основное свойство алгебраической дроби''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Основное свойство алгебраической дроби'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| | + | '''Основное свойство алгебраической дроби'''<br> |
| | | | |
| | + | <br>Вам известно, что значение '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|обыкновенной дроби]]''' не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. |
| | | | |
| - | ''' ОСНОВНОЕ СВОЙСТВО АЛГЕБРАИЧЕСКОЙ ДРОБИ '''<br>
| + | Например: [[Image:11-06-17.jpg|Дроби]] (и числитель и знаменатель мы одновременно умножили на одно и то же число 4; значение дроби не изменилось);[[Image:11-06-18.jpg|Дроби]] (и числитель и знаменатель мы одно временно разделили на одно и то же число 11; значение дроби не определенном смысле обобщение обыкновенной дроби; над алгебраическими дробями можно осуществлять преобразования, аналогичные тем, которые мы только что указали для обыкновенных дробей. Эти преобразования можно описать так: |
| | | | |
| - | <br>Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
| + | ''1. И числитель и '''[[Задачі до уроку на тему «Додавання і віднімання дробів з різними знаменниками»|знаменатель]]''' алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби. <br>'' |
| | | | |
| - | Например: <br>
| + | ''2. И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби, его называют '''[[Основна властивість раціональних дробів. Скорочення раціональних дробів і зведення їх до нового знаменника. Презентація уроку|сокращением]]''' алгебраической дроби. ''<br> |
| | | | |
| - | [[Image:11-06-17.jpg]]<br><br> (и числитель и знаменатель мы одновременно умножили на одно и то же число 4; значение дроби не изменилось);
| + | <br> |
| | | | |
| - | [[Image:11-06-18.jpg]]<br> | + | <u>'''Сформулированные правила представляют собой основное свойство алгебраической дроби.'''</u><br>Пользуясь основным свойством алгебраической дроби, можно дробь —[[Image:11-06-19.jpg|Дробь]] заменить (если, конечно, в этом есть необходимость) дробью [[Image:11-06-20.jpg|Дробь]] (числитель и знаменатель одновременно умножили на х - 2) или дробью [[Image:11-06-21.jpg|Дробь]] (числитель и знаменатель одновременно умножили на 2х). Напротив, пользуясь основным свойством '''[[Упражнения: Основные понятия-1 (8 класс)|алгебраической дроби]]''', можно заменить дробь [[Image:11-06-21.jpg|Дробь]] более простой дробью —[[Image:11-06-19.jpg|Дробь]] (числитель и знаменатель одновременно разделили на 2х, т. е. сократили дробь). |
| | | | |
| - | (и числитель и знаменатель мы одно временно разделили на одно и то же число 11; значение дроби не определенном смысле обобщение обыкновенной дро- <br>би; над алгебраическими дробями можно осуществлять преобразования, аналогичные тем, которые мы только что указали для обыкновенных дробей. Эти преобразования можно описать так:
| + | '''Пример'''. Преобразовать заданные дроби так, чтобы получились дроби с одинаковыми знаменателями: |
| | | | |
| - | ''1. И числитель и знаменатель алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби. <br>''
| + | [[Image:11-06-22.jpg|320px|Задание]] |
| | | | |
| - | ''2. И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби, его называют сокращением алгебраической дроби. ''<br>
| + | <br>Р е ш е н и е. а) Имеем: |
| | | | |
| - | '''Сформулированные правила представляют собой основное свойство алгебраической дроби. '''<br>Пользуясь основным свойством алгебраической дроби, можно дробь —[[Image:11-06-19.jpg]] заменить (если, конечно, в этом есть необходимость) дробью [[Image:11-06-20.jpg]] (числитель и знаменатель одновременно умножили на х - 2) или дробью [[Image:11-06-21.jpg]] (числитель и знаменатель одновременно умножили на 2х). Напротив, пользуясь основным свойством алгебраической дроби, можно заменить дробь [[Image:11-06-21.jpg]] более простой дробью —г (числитель и знаменатель од- <br>новременно разделили на 2х, т. е. сократили дробь). <br>Пример. Преобразовать заданные дроби так, чтобы по- <br>лучились дроби с одинаковыми знаменателями: <br>2а ЗЪ а а2 х х <br>а) ~а~ и ~с~ > б) 772" И —з" ! В) <br>Р е ш е н и е. а) Имеем: <br>2а _ 2а-5 _ 10а <br>3 ~ ~яЖ ~ 15 <br>и <br>3-5 <br>36 = ЗЬ-3 = 96 <br>5 ~ 5-3 15 ' <br>Дроби приведены к одинаковому знаменателю (обычно гово- <br>рят «к общему знаменателю»). Для этого пришлось числитель и <br>знаменатель первой дроби умножить на дополнительный мно- <br>житель 5, а числитель и знаменатель второй дроби — на допол- <br>нительный множитель 3; сделать это позволяет основное свой- <br>ство дроби. <br>б) Имеем <br>Заб <br>д-ЗЬ <br>а2-2 <br>2а2 <br>1263 <br>Дроби приведены к общему знаменателю 12Ь3 с помощью до- <br>полнительных множителей соответственно ЪЪ и 2. <br>в) Имеем <br>X <br>х+у <br>X <br>Х-У <br>х(х-у) <br>(х+у)(х-у) <br>х(х+у) <br>(х-у)(х+у) <br>х -ху _ <br>х2+ху <br>9 9 • <br>х -у <br>Дроби приведены к общему знаменателю х2 - у2 с помощью <br>дополнительных множителей соответственно х - у и х + у. <¦] <br>Приводя в этом примере алгебраические дроби к общему зна- <br>менателю, мы заменяли одну алгебраическую дробь другой дро- <br>бью, тождественно равной первой. Однако если при сокраще- <br>нии дроби мы ее упрощаем, то в рассмотренном примере каж- <br>дая дробь заменялась более сложной. Наверное у вас возник воп- <br>рос: а нужно ли такое «усложняющее» преобразование? <br>Оказывается, нужно, и в этом мы с вами скоро убедимся. <br>С основным свойством алгебраической дроби связаны прави- <br>ла изменения знаков у числителя и знаменателя. Так, имеет ме- <br>сто равенство <br>а-Ъ Ь-а <br>здесь числитель и знаменатель первой дроби мы одновременно <br>умножили на одно и то же число - 1. <br>Если же изменить знаки только в числителе <br>или только в знаменателе, то следует изменить <br>знак и перед дробью: <br>а-Ь _ -(Ь-а) Ь-а <br>а-Ъ <br>c-d <br>а-Ъ <br>c-d -(d-c) <br>c-d' <br>а-Ъ <br>d-c ' <br>§ 3. СЛОЖЕНИЕ И <br><br><br><br>
| + | [[Image:11-06-23.jpg|140px|Задание]]<br>Дроби приведены к одинаковому знаменателю (обычно говорят «к общему знаменателю»). Для этого пришлось числитель и знаменатель первой дроби умножить на дополнительный множитель 5, а числитель и знаменатель второй дроби — на дополнительный множитель 3; сделать это позволяет основное свойство дроби. |
| | | | |
| - | <br> | + | б) Имеем |
| | + | |
| | + | [[Image:11-06-24.jpg|140px|Задание]]<br><br>Дроби приведены к общему знаменателю 12b<sup>3</sup> с помощью дополнительных множителей соответственно 3b и 2. |
| | + | |
| | + | в) Имеем |
| | + | |
| | + | [[Image:11-06-25.jpg|240px|Задание]]<br><br>Дроби приведены к общему знаменателю х<sup>2</sup> - у<sup>2</sup> с помощью дополнительных множителей соответственно х - у и х + у. |
| | + | |
| | + | Приводя в этом примере алгебраические дроби к общему знаменателю, мы заменяли одну алгебраическую дробь другой дробью, тождественно равной первой. Однако если при сокращении дроби мы ее упрощаем, то в рассмотренном примере каждая дробь заменялась более сложной. Наверное у вас возник вопрос: а нужно ли такое «усложняющее» '''[[Преобразование рациональных выражений|преобразование]]'''? |
| | + | |
| | + | Оказывается, нужно, и в этом мы с вами скоро убедимся. |
| | + | |
| | + | С основным свойством алгебраической дроби связаны правила изменения знаков у числителя и знаменателя. Так, имеет место равенство[[Image:11-06-26.jpg|Равенство]] здесь числитель и знаменатель первой дроби мы одновременно умножили на одно и то же число - 1. |
| | + | |
| | + | Если же изменить знаки только в числителе или только в знаменателе, то следует изменить знак и перед дробью: |
| | + | |
| | + | [[Image:11-06-27.jpg|240px|Задание]]<br> |
| | + | |
| | + | <br> |
| | + | |
| | + | ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' |
| | + | |
| | + | <br> |
| | | | |
| | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса [[Математика|скачать]]</sub> | | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса [[Математика|скачать]]</sub> |
| Строка 32: |
Строка 56: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Приводя в этом примере алгебраические дроби к общему знаменателю, мы заменяли одну алгебраическую дробь другой дробью, тождественно равной первой. Однако если при сокращении дроби мы ее упрощаем, то в рассмотренном примере каждая дробь заменялась более сложной. Наверное у вас возник вопрос: а нужно ли такое «усложняющее» преобразование?
Оказывается, нужно, и в этом мы с вами скоро убедимся.
С основным свойством алгебраической дроби связаны правила изменения знаков у числителя и знаменателя. Так, имеет место равенство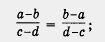 здесь числитель и знаменатель первой дроби мы одновременно умножили на одно и то же число - 1.
здесь числитель и знаменатель первой дроби мы одновременно умножили на одно и то же число - 1.
Если же изменить знаки только в числителе или только в знаменателе, то следует изменить знак и перед дробью:
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.