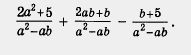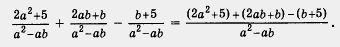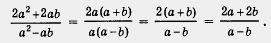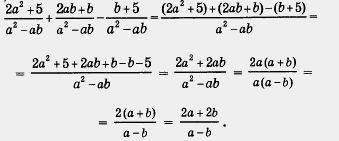|
|
| (1 промежуточная версия не показана) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сложение? вычитание алгебраических дробей с одинаковыми знаменателями </metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сложение, вычитание алгебраических дробей с одинаковыми знаменателями, обыкновенные дроби, алгебраическую дробь, преобразований</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Сложение и вычитание алгебраических дробей с одинаковыми знаменателями''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Сложение и вычитание алгебраических дробей с одинаковыми знаменателями'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| | + | '''Сложение и вычитание алгебраических дробей с одинаковыми знаменателями'''<br> |
| | | | |
| | + | <br>Алгебраические дроби с одинаковыми знаменателями складывают и вычитают по тому же правилу, что и '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|обыкновенные дроби]]''': |
| | | | |
| - | '''СЛОЖЕНИЕ И ВЫЧИТАНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ '''<br>
| + | [[Image:11-06-28.jpg|180px|Задание]]<br><br>т. е. составляют соответствующую алгебраическую [http://xvatit.com/busines/ '''сумму'''] числителей, а знаменатель оставляют без изменений. |
| | | | |
| - | <br>Алгебраические дроби с одинаковыми знаменателями складывают и вычитают по тому же правилу, что и обыкновенные дроби: | + | '''Пример.''' Выполнить действия: <br> |
| | | | |
| - | [[Image:11-06-28.jpg]]<br><br>т. е. составляют соответствующую алгебраическую сумму числителей, а знаменатель оставляют без изменений. | + | [[Image:11-06-29.jpg|240px|Задание]]<br><br>Решение. Применив правило сложения и вычитания алгебраических дробей, получим |
| | | | |
| - | '''Пример.''' Выполнить действия: <br>
| + | [[Image:11-06-30.jpg|420px|Задание]]<br><br>Теперь можно упростить числитель, выполнив обычным образом соответствующие операции над многочленами: |
| - | | + | |
| - | [[Image:11-06-29.jpg]]<br><br>Решение. Применив правило сложения и вычитания алгебраических дробей, получим
| + | |
| - | | + | |
| - | [[Image:11-06-30.jpg]]<br><br>Теперь можно упростить числитель, выполнив обычным образом соответствующие операции над многочленами: | + | |
| | | | |
| | (2а<sup>2</sup> + 5) +(2аb + b) - (b + 5) = <br>= 2а<sup>2</sup> + 5 + 2аb + b - b - 5 = 2а<sup>2</sup> + 2аb. | | (2а<sup>2</sup> + 5) +(2аb + b) - (b + 5) = <br>= 2а<sup>2</sup> + 5 + 2аb + b - b - 5 = 2а<sup>2</sup> + 2аb. |
| | | | |
| - | Таким образом, заданную алгебраическую сумму трех дробей нам удалось преобразовать в дробь —[[Image:11-06-31.jpg]] . <br>А теперь вспомните то, что мы говорили в предыдущем параграфе: получив алгебраическую дробь, нужно посмотреть, нельзя ли ее сократить. | + | Таким образом, заданную алгебраическую сумму трех дробей нам удалось преобразовать в дробь —[[Image:11-06-31.jpg|Задание]] . <br>А теперь вспомните то, что мы говорили в предыдущем параграфе: получив '''[[Упражнения: Основные понятия-1 (8 класс)|алгебраическую дробь]]''', нужно посмотреть, нельзя ли ее сократить. |
| | | | |
| | Имеем | | Имеем |
| | | | |
| - | [[Image:11-06-32.jpg]]<br><br>Приведем теперь решение рассмотренного примера без комментариев (как это вы будете делать у себя в тетрадях): | + | [[Image:11-06-32.jpg|320px|Задание]]<br><br>Приведем теперь решение рассмотренного примера без комментариев (как это вы будете делать у себя в тетрадях): |
| | | | |
| - | [[Image:11-06-33.jpg]]<br><br>Как видите, в результате преобразований получилось более простое алгебраическое выражение, чем было задано в условии примера. Именно в упрощении и состоит цель преобразований, поэтому часто, вместо словосочетания «выполнить действия», используют словосочетание «упростить выражение». <br><br><br><sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> | + | [[Image:11-06-33.jpg|420px|Задание]]<br><br>Как видите, в результате '''[[Преобразование рациональных выражений|преобразований]]''' получилось более простое алгебраическое выражение, чем было задано в условии примера. Именно в упрощении и состоит цель преобразований, поэтому часто, вместо словосочетания «выполнить действия», используют словосочетание «упростить выражение». |
| | + | |
| | + | ''<br>Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br><br><sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Таким образом, заданную алгебраическую сумму трех дробей нам удалось преобразовать в дробь —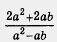 .
.
А теперь вспомните то, что мы говорили в предыдущем параграфе: получив алгебраическую дробь, нужно посмотреть, нельзя ли ее сократить.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.