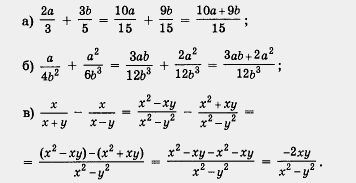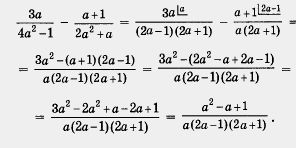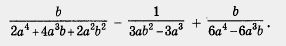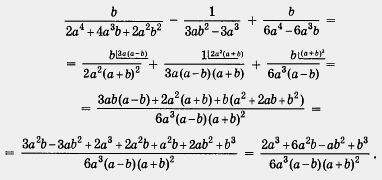|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сложение, вычитание алгебраических дробей с разными знаменателями</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сложение, вычитание алгебраических дробей с разными знаменателями, алгебраических дробей, знаменатель, дроби, коэффициентах, алгоритм, выражение, таблицы</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Сложение и вычитание алгебраических дробей с разными знаменателями''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Сложение и вычитание алгебраических дробей с разными знаменателями'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <br>
| + | '''Сложение и вычитание алгебраических дробей с разными знаменателями'''<br> |
| - | | + | |
| - | '''СЛОЖЕНИЕ И ВЫЧИТАНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ '''<br> | + | |
| | | | |
| - | <br>Сложение и вычитание алгебраических дробей с разными знаменателями выполняют по тому же алгоритму, что используется для сложения и вычитания обыкновенных дробей с разными знаменателями: сначала приводят дроби к общему знаменателю с помощью соответствующих дополнительных множи- <br>телей, а затем складывают или вычитают полученные дроби с одинаковыми знаменателями по правилу из § 3. Можно сформулировать алгоритм, охватывающий любые случаи сложения (вычитания) алгебраических дробей. | + | <br>Сложение и вычитание '''[[Упражнения: Основные понятия-1 (8 класс)|алгебраических дробей]]''' с разными знаменателями выполняют по тому же алгоритму, что используется для сложения и вычитания обыкновенных дробей с разными знаменателями: сначала приводят дроби к общему знаменателю с помощью соответствующих дополнительных множителей, а затем складывают или вычитают полученные дроби с одинаковыми знаменателями по правилу из § 3. Можно сформулировать алгоритм, охватывающий любые случаи сложения (вычитания) алгебраических дробей. |
| | | | |
| | '''Алгоритм сложения (вычитания) алгебраических дробей '''<br> | | '''Алгоритм сложения (вычитания) алгебраических дробей '''<br> |
| | | | |
| - | [[Image:11-06-34.jpg]]<br><br>'''Пример 1.''' Выполнить действия: | + | [[Image:11-06-34.jpg|480px|Алгоритм сложения (вычитания)]]<br><br>'''Пример 1.''' Выполнить действия: |
| | | | |
| - | [[Image:11-06-35.jpg]]<br><br>Решение. Для каждой пары заданных здесь алгебраических дробей общий знаменатель был найден выше, в примере из § 2. Опираясь на указанный пример, получаем: | + | [[Image:11-06-35.jpg|320px|Задание]]<br><br>Решение. Для каждой пары заданных здесь алгебраических дробей общий '''[[Задачі до уроку на тему «Додавання і віднімання дробів з різними знаменниками»|знаменатель]]''' был найден выше, в примере из § 2. Опираясь на указанный пример, получаем: |
| | | | |
| - | [[Image:11-06-36.jpg]]<br><br>Самое трудное в приведенном алгоритме — это, конечно, первый шаг: отыскание общего знаменателя и приведение дробей к общему знаменателю. В примере 1 вы этой трудности, может быть, не ощутили, поскольку мы воспользовались готовыми результатами из § 2. | + | [[Image:11-06-36.jpg|320px|Задание]]<br><br>Самое трудное в приведенном алгоритме — это, конечно, первый шаг: отыскание общего знаменателя и приведение дробей к общему знаменателю. В примере 1 вы этой трудности, может быть, не ощутили, поскольку мы воспользовались готовыми результатами из § 2. |
| | | | |
| - | Чтобы выработать правило отыскания общего знаменателя, проанализируем пример 1. <br>Для дробей [[Image:11-06-37.jpg]] общий знаменатель есть число 15 оно делится и на 3 и на 5, является их общим кратным (даже наименьшим общим кратным). <br>Для дробей —[[Image:11-06-38.jpg]] общим знаменателем является одночлен 12b<sup>3</sup>. Он делится и на 4b<sup>2</sup> и на 6b<sup>3</sup> , т. е. на оба одночлена, служащие знаменателями дробей. | + | Чтобы выработать правило отыскания общего знаменателя, проанализируем пример 1. <br>Для дробей [[Image:11-06-37.jpg|Дроби]] общий знаменатель есть число 15 оно делится и на 3 и на 5, является их общим кратным (даже наименьшим общим кратным). <br>Для дробей —[[Image:11-06-38.jpg|Дроби]] общим знаменателем является одночлен 12b<sup>3</sup>. Он делится и на 4b<sup>2</sup> и на 6b<sup>3</sup> , т. е. на оба одночлена, служащие знаменателями дробей. |
| | | | |
| - | Обратите внимание: число 12 — наименьшее общее кратное чисел 4 и 6. Переменная b входит в знаменатель первой дроби с показателем 2, в знаменатель <br>второй дроби — с показателем 3. Это наибольшее значение показателя 3 фигурирует в общем знаменателе. <br>Для дробей | + | Обратите внимание: число 12 — наименьшее общее кратное чисел 4 и 6. Переменная b входит в знаменатель первой '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|дроби]]''' с показателем 2, в знаменатель <br>второй дроби — с показателем 3. Это наибольшее значение показателя 3 фигурирует в общем знаменателе. <br>Для дробей[[Image:11-06-39.jpg|Дроби]] общим знаменателем служит произведение (х + у)(х - у) — оно делится и на знаменатель х + у и на знаменатель х-у. |
| | | | |
| - | [[Image:11-06-39.jpg]]<br>общим знаменателем служит произведение (х + у)(х - у) — оно делится и на знаменатель х + у и на знаменатель х-у.
| + | При отыскании общего знаменателя приходится, естественно, все заданные знаменатели разлагать на множители (если это не было подготовлено в условии). А далее следует провести работу по этапам: найти наименьшее общее кратное для числовых коэффициентов (речь идет о целочисленных '''[[Задачі: Переставна і сполучна властивості множення. Коефіцієнт|коэффициентах]]'''), определить для каждого несколько раз встречающегося буквенного множителя наибольший показатель степени, собрать все это в одно произведение. |
| - | | + | |
| - | При отыскании общего знаменателя приходится, естественно, все заданные знаменатели разлагать на множители (если это не было подготовлено в условии). А далее следует провести работу по этапам: найти наименьшее общее кратное для числовых коэффициентов (речь идет о целочисленных коэффициентах), определить для каждого несколько раз встречающегося буквенного множителя наибольший показатель степени, собрать все это в одно произведение. | + | |
| | | | |
| | Теперь можно оформить соответствующий алгоритм. | | Теперь можно оформить соответствующий алгоритм. |
| | | | |
| - | <br>'''Алгоритм отыскания общего знаменателя для нескольких алгебраических дробей '''
| + | '''Алгоритм отыскания общего знаменателя для нескольких алгебраических дробей ''' |
| | | | |
| - | [[Image:11-06-40.jpg]]<br><br>Прежде чем двигаться дальше, попробуйте применить этот алгоритм к обоснованию поиска общего знаменателя для алгебраических дробей из примера 1. <br>'''''Замечание.''''' На самом деле общих знаменателей для двух алгебраических дробей можно найти сколько угодно. Например, для дробей [[Image:11-06-41.jpg]] общим <br>знаменателем может быть и число 30, и число 60, и даже одночлен 15а2Ь. Дело в том, что и 30, и 60, и 15а<sup>2</sup>b можно разделить как на 3, так и на 5. Для <br>дробей — [[Image:11-06-42.jpg]]<br>общим знаменателем, кроме найденного выше одночлена 12b , может быть и 24b<sup>3</sup> и 48а<sup>2</sup>b<sup>4</sup>. Чем же одночлен 12b<sup>3</sup> лучше, чем 24b<sup>3</sup>, чем 48а<sup>2</sup>b<sup>4</sup>? Он проще (по виду). Его иногда называют даже не общим знаменателем, а наименьшим общим знаменателем. Таким образом, приведенный алгоритм — это алгоритм <br>отыскания самого простого из общих знаменателей нескольких алгебраических дробей, алгоритм отыскания наименьшего общего знаменателя. | + | [[Image:11-06-40.jpg|480px|Алгоритм отыскания общего знаменателя]]<br><br>Прежде чем двигаться дальше, попробуйте применить этот '''[[Урок 4. Программа действий. Алгоритм|алгоритм]]''' к обоснованию поиска общего знаменателя для алгебраических дробей из примера 1. <br>'''''Замечание.''''' На самом деле общих знаменателей для двух алгебраических дробей можно найти сколько угодно. Например, для дробей [[Image:11-06-41.jpg|Дроби]] общим знаменателем может быть и число 30, и число 60, и даже одночлен 15а2Ь. Дело в том, что и 30, и 60, и 15а<sup>2</sup>b можно разделить как на 3, так и на 5. Для дробей — [[Image:11-06-42.jpg|Дроби]]<br>общим знаменателем, кроме найденного выше одночлена 12b , может быть и 24b<sup>3</sup> и 48а<sup>2</sup>b<sup>4</sup>. Чем же одночлен 12b<sup>3</sup> лучше, чем 24b<sup>3</sup>, чем 48а<sup>2</sup>b<sup>4</sup>? Он проще (по виду). Его иногда называют даже не общим знаменателем, а наименьшим общим знаменателем. Таким образом, приведенный алгоритм — это алгоритм отыскания самого простого из общих знаменателей нескольких алгебраических дробей, алгоритм отыскания наименьшего общего знаменателя. |
| | | | |
| - | Снова вернемся к примеру 1, а. Чтобы сложить алгебраические дроби [[Image:11-06-43.jpg]] , надо было не только найти общий знаменатель (число 15), но и отыскать для каждой из дробей дополнительные множители, которые позволили бы привести дроби к общему знаменателю. Для дроби [[Image:11-06-44.jpg]] таким дополнительным мно- <br>жителем служит число 5 (числитель и знаменатель этой дроби умножили дополнительно на 5), для дроби [[Image:11-06-45.jpg]] число 3 (числитель и знаменатель этой дроби умножили дополнительно на 3). | + | Снова вернемся к примеру 1, а. Чтобы сложить алгебраические дроби [[Image:11-06-43.jpg|Дроби]] , надо было не только найти общий знаменатель (число 15), но и отыскать для каждой из дробей дополнительные множители, которые позволили бы привести дроби к общему знаменателю. Для дроби [[Image:11-06-44.jpg]] таким дополнительным множителем служит число 5 (числитель и знаменатель этой дроби умножили дополнительно на 5), для дроби [[Image:11-06-45.jpg]] число 3 (числитель и знаменатель этой дроби умножили дополнительно на 3). |
| | | | |
| | Дополнительный множитель есть частное от деления общего знаменателя на знаменатель данной дроби. <br>Обычно используют следующую запись: | | Дополнительный множитель есть частное от деления общего знаменателя на знаменатель данной дроби. <br>Обычно используют следующую запись: |
| | | | |
| - | [[Image:11-06-46.jpg]]<br>Снова вернемся к примеру 1,6. Общим знаменателем для дробей [[Image:11-06-47.jpg]] является одночлен 12b<sup>3</sup>. Дополнительный множитель для первой дроби равен Зb (поскольку 12b<sup>3</sup> : 4b<sup>2</sup> = З<sup>Ь</sup>), для второй дроби он равен 2 (поскольку 12b<sup>3</sup> : 6b<sup>3</sup> = 2). Значит, решение примера 1,6 можно оформить так: | + | [[Image:11-06-46.jpg|240px|Задание]]<br>Снова вернемся к примеру 1,6. Общим знаменателем для дробей [[Image:11-06-47.jpg|Дроби]] является одночлен 12b<sup>3</sup>. Дополнительный множитель для первой дроби равен Зb (поскольку 12b<sup>3</sup> : 4b<sup>2</sup> = З<sup>Ь</sup>), для второй дроби он равен 2 (поскольку 12b<sup>3</sup> : 6b<sup>3</sup> = 2). Значит, решение примера 1,6 можно оформить так: |
| | | | |
| - | [[Image:11-06-48.jpg]]<br>Выше был сформулирован алгоритм отыскания общего знаменателя для нескольких алгебраических дробей. Но опыт показывает, что этот алгоритм не всегда бывает понятен учащимся, поэтому мы дадим несколько видоизмененную формулировку. | + | [[Image:11-06-48.jpg|180px|Задание]]<br>Выше был сформулирован алгоритм отыскания общего знаменателя для нескольких алгебраических дробей. Но опыт показывает, что этот алгоритм не всегда бывает понятен учащимся, поэтому мы дадим несколько видоизмененную формулировку. |
| | | | |
| - | '''Правило приведения алгебраических дробей к общему знаменателю ''' | + | '''Правило приведения алгебраических дробей к общему знаменателю ''' |
| | | | |
| - | '''[[Image:11-06-49.jpg]]''' | + | '''[[Image:11-06-49.jpg|480px|Правило приведения алгебраических дробей к общему знаменателю]]'''<br>'''<br>Пример 2.''' Упростить '''[[Основное свойство алгебраической дроби|выражение]]''' |
| | | | |
| - | <br>'''<br>Пример 2.''' Упростить выражение | + | [[Image:11-06-50.jpg|Задание]]<br><br>Решение. <br><u>'''Первый этап.'''</u> Найдем общий знаменатель и дополнительные множители. |
| | | | |
| - | [[Image:11-06-50.jpg]]<br><br>Решение. <br><u>'''Первый этап.'''</u> Найдем общий знаменатель и дополнительные множители.
| + | Имеем <br>4а<sup>2</sup> - 1 = (2а - 1) (2а + 1), <br>2а<sup>2</sup> + а = а(2а + 1). |
| | | | |
| - | Имеем <br>4а<sup>2</sup> - 1 = (2а - 1) (2а + 1), <br>2а<sup>2</sup> + а = а(2а + 1). <br>Первый знаменатель берем целиком, а из второго — добавляем множитель а, которого нет в первом знаменателе. Получим общий знаменатель
| + | Первый знаменатель берем целиком, а из второго — добавляем множитель а, которого нет в первом знаменателе. Получим общий знаменатель |
| | | | |
| | a(2a - 1) (2a +1). | | a(2a - 1) (2a +1). |
| | | | |
| - | '''Удобно расположить записи в виде таблицы: ''' | + | '''Удобно расположить записи в виде '''[[Складання таблиці додавання і віднімання 1. Ілюстрації|'''таблицы''']]''': '''<br> |
| | | | |
| | + | [[Image:11-06-51.jpg|480px|Задание]]<br><u>'''Второй этап.'''</u><br>Выполним преобразования: |
| | | | |
| - | | + | [[Image:11-06-52.jpg|320px|Задание]]<br><br>При наличии некоторого опыта первый этап можно не выделять, выполняя его одновременно со вторым этапом. |
| - | [[Image:11-06-51.jpg]]
| + | |
| - | | + | |
| - | <br><u>'''Второй этап.'''</u><br>Выполним преобразования:
| + | |
| - | | + | |
| - | [[Image:11-06-52.jpg]]<br><br>При наличии некоторого опыта первый этап можно не выделять, выполняя его одновременно со вторым этапом. | + | |
| | | | |
| | В заключение рассмотрим более сложный пример (для желающих). | | В заключение рассмотрим более сложный пример (для желающих). |
| Строка 67: |
Строка 59: |
| | <u>'''Пример 3'''</u>. Упростить выражение | | <u>'''Пример 3'''</u>. Упростить выражение |
| | | | |
| - | [[Image:11-06-53.jpg]]<br><br>Решение. <br><u>Первый этап. </u><br>Разложим все знаменатели на множители: | + | [[Image:11-06-53.jpg|320px|Задание]]<br><br>Решение. <br><u>Первый этап. </u><br>Разложим все знаменатели на множители: |
| | | | |
| | 1) 2а<sup>4</sup> + 4а<sup>3</sup>b + 2a<sup>2</sup>b<sup>2</sup> = 2а<sup>2</sup> (а<sup>2</sup> + 2аb + b<sup>2</sup>) = 2а<sup>2</sup> (а + b)<sup>2</sup>; | | 1) 2а<sup>4</sup> + 4а<sup>3</sup>b + 2a<sup>2</sup>b<sup>2</sup> = 2а<sup>2</sup> (а<sup>2</sup> + 2аb + b<sup>2</sup>) = 2а<sup>2</sup> (а + b)<sup>2</sup>; |
| Строка 77: |
Строка 69: |
| | Первый знаменатель берем целиком, из второго возьмем недостающие множители 3 и b - а (или a — b), из третьего — недостающий множитель а (поскольку третий знаменатель содержит множитель а<sup>3</sup>). | | Первый знаменатель берем целиком, из второго возьмем недостающие множители 3 и b - а (или a — b), из третьего — недостающий множитель а (поскольку третий знаменатель содержит множитель а<sup>3</sup>). |
| | | | |
| - | '''Алгебраические дроби''' | + | '''Алгебраические дроби''' |
| | | | |
| - | [[Image:11-06-54.jpg]]<br><br>Заметим, что если у дополнительного множителя появляется знак «-», то его обычно ставят перед всей дробью, т. е. перед второй дробью придется поменять знак. | + | [[Image:11-06-54.jpg|480px|Алгебраические дроби]]<br><br>Заметим, что если у дополнительного множителя появляется знак «-», то его обычно ставят перед всей дробью, т. е. перед второй дробью придется поменять знак. |
| | | | |
| | <u>'''Второй этап.'''</u><br>Выполним преобразования: | | <u>'''Второй этап.'''</u><br>Выполним преобразования: |
| | | | |
| - | [[Image:11-06-55.jpg]]<br><br>Отметим, что замена выражения, данного в примере 3, той алгебраической дробью, которая получилась в результате, есть тождественное преобразование при допустимых значениях переменных. В данном случае допустимыми являются любые значения переменных а и Ь, кроме a = 0, a = b, a = - b (в этих <br>случаях знаменатели обращаются в нуль). <br><br><br><br> | + | [[Image:11-06-55.jpg|320px|Задание]]<br><br>Отметим, что замена выражения, данного в примере 3, той алгебраической дробью, которая получилась в результате, есть тождественное преобразование при допустимых значениях переменных. В данном случае допустимыми являются любые значения переменных а и Ь, кроме a = 0, a = b, a = - b (в этих <br>случаях знаменатели обращаются в нуль). <br><br>''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br><br> |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> |
| Строка 90: |
Строка 82: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 06:32, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями выполняют по тому же алгоритму, что используется для сложения и вычитания обыкновенных дробей с разными знаменателями: сначала приводят дроби к общему знаменателю с помощью соответствующих дополнительных множителей, а затем складывают или вычитают полученные дроби с одинаковыми знаменателями по правилу из § 3. Можно сформулировать алгоритм, охватывающий любые случаи сложения (вычитания) алгебраических дробей.
Алгоритм сложения (вычитания) алгебраических дробей

Пример 1. Выполнить действия:
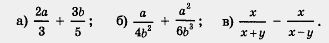
Решение. Для каждой пары заданных здесь алгебраических дробей общий знаменатель был найден выше, в примере из § 2. Опираясь на указанный пример, получаем:
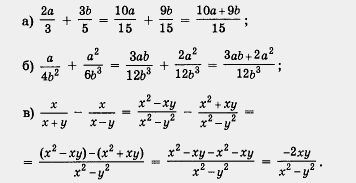
Самое трудное в приведенном алгоритме — это, конечно, первый шаг: отыскание общего знаменателя и приведение дробей к общему знаменателю. В примере 1 вы этой трудности, может быть, не ощутили, поскольку мы воспользовались готовыми результатами из § 2.
Чтобы выработать правило отыскания общего знаменателя, проанализируем пример 1.
Для дробей 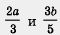 общий знаменатель есть число 15 оно делится и на 3 и на 5, является их общим кратным (даже наименьшим общим кратным). общий знаменатель есть число 15 оно делится и на 3 и на 5, является их общим кратным (даже наименьшим общим кратным).
Для дробей —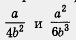 общим знаменателем является одночлен 12b3. Он делится и на 4b2 и на 6b3 , т. е. на оба одночлена, служащие знаменателями дробей. общим знаменателем является одночлен 12b3. Он делится и на 4b2 и на 6b3 , т. е. на оба одночлена, служащие знаменателями дробей.
Обратите внимание: число 12 — наименьшее общее кратное чисел 4 и 6. Переменная b входит в знаменатель первой дроби с показателем 2, в знаменатель
второй дроби — с показателем 3. Это наибольшее значение показателя 3 фигурирует в общем знаменателе.
Для дробей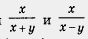 общим знаменателем служит произведение (х + у)(х - у) — оно делится и на знаменатель х + у и на знаменатель х-у. общим знаменателем служит произведение (х + у)(х - у) — оно делится и на знаменатель х + у и на знаменатель х-у.
При отыскании общего знаменателя приходится, естественно, все заданные знаменатели разлагать на множители (если это не было подготовлено в условии). А далее следует провести работу по этапам: найти наименьшее общее кратное для числовых коэффициентов (речь идет о целочисленных коэффициентах), определить для каждого несколько раз встречающегося буквенного множителя наибольший показатель степени, собрать все это в одно произведение.
Теперь можно оформить соответствующий алгоритм.
Алгоритм отыскания общего знаменателя для нескольких алгебраических дробей

Прежде чем двигаться дальше, попробуйте применить этот алгоритм к обоснованию поиска общего знаменателя для алгебраических дробей из примера 1.
Замечание. На самом деле общих знаменателей для двух алгебраических дробей можно найти сколько угодно. Например, для дробей 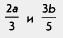 общим знаменателем может быть и число 30, и число 60, и даже одночлен 15а2Ь. Дело в том, что и 30, и 60, и 15а2b можно разделить как на 3, так и на 5. Для дробей — общим знаменателем может быть и число 30, и число 60, и даже одночлен 15а2Ь. Дело в том, что и 30, и 60, и 15а2b можно разделить как на 3, так и на 5. Для дробей — 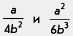
общим знаменателем, кроме найденного выше одночлена 12b , может быть и 24b3 и 48а2b4. Чем же одночлен 12b3 лучше, чем 24b3, чем 48а2b4? Он проще (по виду). Его иногда называют даже не общим знаменателем, а наименьшим общим знаменателем. Таким образом, приведенный алгоритм — это алгоритм отыскания самого простого из общих знаменателей нескольких алгебраических дробей, алгоритм отыскания наименьшего общего знаменателя.
Снова вернемся к примеру 1, а. Чтобы сложить алгебраические дроби 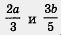 , надо было не только найти общий знаменатель (число 15), но и отыскать для каждой из дробей дополнительные множители, которые позволили бы привести дроби к общему знаменателю. Для дроби , надо было не только найти общий знаменатель (число 15), но и отыскать для каждой из дробей дополнительные множители, которые позволили бы привести дроби к общему знаменателю. Для дроби 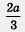 таким дополнительным множителем служит число 5 (числитель и знаменатель этой дроби умножили дополнительно на 5), для дроби таким дополнительным множителем служит число 5 (числитель и знаменатель этой дроби умножили дополнительно на 5), для дроби 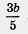 число 3 (числитель и знаменатель этой дроби умножили дополнительно на 3). число 3 (числитель и знаменатель этой дроби умножили дополнительно на 3).
Дополнительный множитель есть частное от деления общего знаменателя на знаменатель данной дроби.
Обычно используют следующую запись:
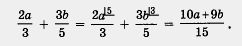
Снова вернемся к примеру 1,6. Общим знаменателем для дробей 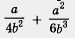 является одночлен 12b3. Дополнительный множитель для первой дроби равен Зb (поскольку 12b3 : 4b2 = ЗЬ), для второй дроби он равен 2 (поскольку 12b3 : 6b3 = 2). Значит, решение примера 1,6 можно оформить так: является одночлен 12b3. Дополнительный множитель для первой дроби равен Зb (поскольку 12b3 : 4b2 = ЗЬ), для второй дроби он равен 2 (поскольку 12b3 : 6b3 = 2). Значит, решение примера 1,6 можно оформить так:
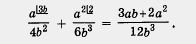
Выше был сформулирован алгоритм отыскания общего знаменателя для нескольких алгебраических дробей. Но опыт показывает, что этот алгоритм не всегда бывает понятен учащимся, поэтому мы дадим несколько видоизмененную формулировку.
Правило приведения алгебраических дробей к общему знаменателю

Пример 2. Упростить выражение
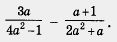
Решение.
Первый этап. Найдем общий знаменатель и дополнительные множители.
Имеем
4а2 - 1 = (2а - 1) (2а + 1),
2а2 + а = а(2а + 1).
Первый знаменатель берем целиком, а из второго — добавляем множитель а, которого нет в первом знаменателе. Получим общий знаменатель
a(2a - 1) (2a +1).
Удобно расположить записи в виде таблицы:

Второй этап.
Выполним преобразования:
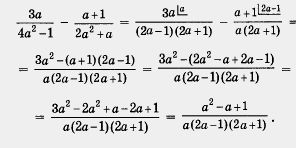
При наличии некоторого опыта первый этап можно не выделять, выполняя его одновременно со вторым этапом.
В заключение рассмотрим более сложный пример (для желающих).
Пример 3. Упростить выражение
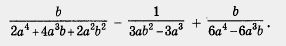
Решение.
Первый этап.
Разложим все знаменатели на множители:
1) 2а4 + 4а3b + 2a2b2 = 2а2 (а2 + 2аb + b2) = 2а2 (а + b)2;
2) 3ab2 - За3 = За (b2 - а2) = За (b - а) (b + а);
3) 6а4-6а3b = 6а3(а- b).
Первый знаменатель берем целиком, из второго возьмем недостающие множители 3 и b - а (или a — b), из третьего — недостающий множитель а (поскольку третий знаменатель содержит множитель а3).
Алгебраические дроби

Заметим, что если у дополнительного множителя появляется знак «-», то его обычно ставят перед всей дробью, т. е. перед второй дробью придется поменять знак.
Второй этап.
Выполним преобразования:
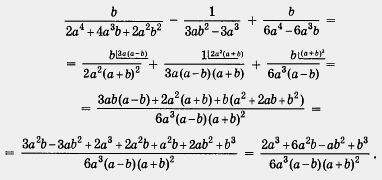
Отметим, что замена выражения, данного в примере 3, той алгебраической дробью, которая получилась в результате, есть тождественное преобразование при допустимых значениях переменных. В данном случае допустимыми являются любые значения переменных а и Ь, кроме a = 0, a = b, a = - b (в этих
случаях знаменатели обращаются в нуль).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|