|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Основные результаты</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Основные результаты, функций, координатной плоскости, графики</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Основные результаты''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Основные результаты''' |
| Строка 5: |
Строка 5: |
| | <br> '''Основные результаты ''' | | <br> '''Основные результаты ''' |
| | | | |
| - | <br> В этой главе мы существенно пополнили <u>запас функций</u>, графики которых теперь умеем строить. | + | <br> В этой главе мы существенно пополнили запас '''[[Функция у = х2 и ее график|функций]]''', графики которых теперь умеем строить. |
| | | | |
| | Если в 7-м классе мы, кроме линейной функции, изучили лишь одну функцию у = х<sup>2</sup>, то теперь знаем, как обстоит дело с функциями [[Image:11-06-177.jpg|120px|Функции]] для любого коэффициента[[Image:11-06-178.jpg]] <br> | | Если в 7-м классе мы, кроме линейной функции, изучили лишь одну функцию у = х<sup>2</sup>, то теперь знаем, как обстоит дело с функциями [[Image:11-06-177.jpg|120px|Функции]] для любого коэффициента[[Image:11-06-178.jpg]] <br> |
| Строка 11: |
Строка 11: |
| | графиком функции у = kx<sup>2</sup> является парабола (с ветвями вверх при k > 0 или вниз при k < 0 и с вершиной в начале координат); | | графиком функции у = kx<sup>2</sup> является парабола (с ветвями вверх при k > 0 или вниз при k < 0 и с вершиной в начале координат); |
| | | | |
| - | графиком функции [[Image:11-06-179.jpg]] (обратная пропорциональность) является гипербола: при k > 0 — с ветвями в первом и третьем координатных углах координатной плоскости; при k < 0 — с ветвями во втором и четвертом координатных углах координатной плоскости.<br> | + | графиком функции [[Image:11-06-179.jpg]] (обратная пропорциональность) является гипербола: при k > 0 — с ветвями в первом и третьем координатных углах координатной плоскости; при k < 0 — с ветвями во втором и четвертом координатных углах '''[[Ілюстрації до теми Координатна площина|координатной плоскости]]'''.<br> |
| | | | |
| | Мы научились строить параболу у = ах<sup>2</sup> +bх + с для любых а, b, с (где [[Image:11-06-180.jpg]]), знаем уравнение ее оси симметрии: [[Image:11-06-181.jpg|Уравнение]].<br> | | Мы научились строить параболу у = ах<sup>2</sup> +bх + с для любых а, b, с (где [[Image:11-06-180.jpg]]), знаем уравнение ее оси симметрии: [[Image:11-06-181.jpg|Уравнение]].<br> |
| | | | |
| - | Мы научились, зная график функции у = f(x), строить графики следующих функций: у = f (х + I), у = f(x) + m, у = f(x + I) + m, у = - f(x).<br> | + | Мы научились, зная график функции у = f(x), строить '''[[Приклади графіків залежностей між величинами|графики]]''' следующих функций: у = f (х + I), у = f(x) + m, у = f(x + I) + m, у = - f(x).<br> |
| | | | |
| | Мы пополнили список свойств функции, которые обычно включают в процедуру чтения графика, двумя новыми свойствами: | | Мы пополнили список свойств функции, которые обычно включают в процедуру чтения графика, двумя новыми свойствами: |
| Строка 25: |
Строка 25: |
| | <br> | | <br> |
| | | | |
| - | ''Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.'' | + | ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.'' |
| | | | |
| | <br> <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub><br> <br> | | <br> <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub><br> <br> |
Текущая версия на 08:29, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Основные результаты
Основные результаты
В этой главе мы существенно пополнили запас функций, графики которых теперь умеем строить.
Если в 7-м классе мы, кроме линейной функции, изучили лишь одну функцию у = х2, то теперь знаем, как обстоит дело с функциями 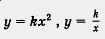 для любого коэффициента
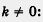
графиком функции у = kx2 является парабола (с ветвями вверх при k > 0 или вниз при k < 0 и с вершиной в начале координат);
графиком функции 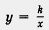 (обратная пропорциональность) является гипербола: при k > 0 — с ветвями в первом и третьем координатных углах координатной плоскости; при k < 0 — с ветвями во втором и четвертом координатных углах координатной плоскости.
Мы научились строить параболу у = ах2 +bх + с для любых а, b, с (где 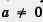 ), знаем уравнение ее оси симметрии:  .
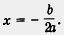Мы научились, зная график функции у = f(x), строить графики следующих функций: у = f (х + I), у = f(x) + m, у = f(x + I) + m, у = - f(x).
Мы пополнили список свойств функции, которые обычно включают в процедуру чтения графика, двумя новыми свойствами:
ограниченность функции снизу;
ограниченность функции сверху.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Математика для 8 класса, учебники и книги по математике скачать, библиотека онлайн
Содержание урока
 конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
