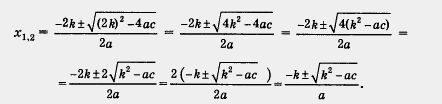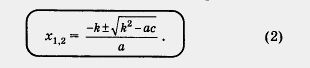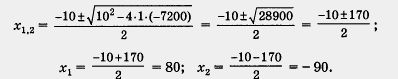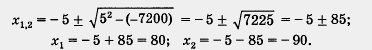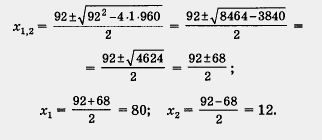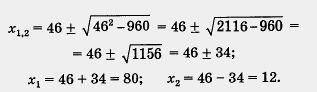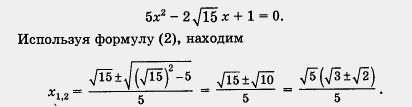|
|
|
| (2 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <p><span class="fck_mw_special" _fck_mw_customtag="true" _fck_mw_tagname="metakeywords">Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Еще одна формула корней квадратного уравнения</span> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Еще одна формула корней квадратного уравнения, корни, формулу, квадратного уравнения</metakeywords> |
| - | </p><p><b><a href="Гипермаркет знаний - первый в мире!">Гипермаркет знаний</a>>><a href="Математика">Математика</a>>><a href="Математика 8 класс">Математика 8 класс</a>>>Математика:Еще одна формула корней квадратного уравнения</b>
| + | |
| - | </p><p><br />
| + | |
| - | </p><p><br />
| + | |
| - | </p><p><b> ЕЩЕ ОДНА ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ </b>
| + | |
| - | </p><p><br />Мы с вами уже привыкли к тому, что корни квадратного уравнения ах<sup>2</sup> + bх + с = 0 находятся по формуле
| + | |
| - | </p><p><img src="/images/1/10/14-06-37.jpg" _fck_mw_filename="14-06-37.jpg" alt="" /><br /><br />(если, конечно, дискриминант D = b<sup>2</sup> — 4ас — неотрицательное число; если же D < О, то приведенная формула не имеет смысла, а квадратное уравнение не имеет корней). <br />Но математики никогда не пройдут мимо возможности облегчить себе вычисления. Они обнаружили, что формулу (1) можно упростить в случае, когда коэффициент b имеет вид b = 2k, в частности, если Ъ есть четное число. <br />В самом деле, пусть у квадратного уравнения ах2 + Ьх + с = О <br />коэффициент Ъ имеет вид Ъ — 2k. Подставив в формулу (1) число 2k вместо b, получим:
| + | |
| - | </p><p><img src="/images/6/61/14-06-38.jpg" _fck_mw_filename="14-06-38.jpg" alt="" /><br /><br />Итак, корни квадратного уравнения ах<sup>2</sup> + + 2kx + с = О можно вычислять по формуле
| + | |
| - | </p><p><img src="/images/9/93/14-06-39.jpg" _fck_mw_filename="14-06-39.jpg" alt="" /><br />Сравните эту формулу с формулой (1). В чем ее преимущества?
| + | |
| - | </p><p>Во-первых, в квадрат возводится не число b, а его половина <img src="/images/8/80/14-06-40.jpg" _fck_mw_filename="14-06-40.jpg" alt="" />
| + | |
| - | </p><p>Во-вторых, вычитается из этого квадрата не 4ас, a просто ас.
| + | |
| - | </p><p>В-третьих, в знаменателе содержится не 2а, а просто а. Как видите, по крайней мере в трех моментах мы облегчаем себе выкладки. Особенно приятно выглядит формула (2) для приведенного квадратного уравнения, т. е. для случая, когда а = 1. Тогда получаем
| + | |
| - | </p><p><img src="/images/0/07/14-06-41.jpg" _fck_mw_filename="14-06-41.jpg" alt="" /><br /><br />Это — формула корней уравнения х<sup>2</sup> + 2kx + с — 0. <br />Вернемся к предыдущему параграфу и еще раз решим некоторые из имеющихся там квадратных уравнений — для сравнения трудоемкости вычислений по старой формуле (формуле (1)) и по новой формуле (формуле(2) или (3)). <br />В примере 1 из § 22 получилось квадратное уравнение х<sup>2</sup> + 10x - 7200 = 0. <br />Мы решали его так:
| + | |
| - | </p><p><img src="/images/9/95/14-06-42.jpg" _fck_mw_filename="14-06-42.jpg" alt="" /><br /><br />А теперь решим то же квадратное уравнение по формуле (3), учитывая, что в данном случае b = 10, т. е. 2k = 10, k = 5. Имеем
| + | |
| - | </p><p><img src="/images/7/76/14-06-43.jpg" _fck_mw_filename="14-06-43.jpg" alt="" /><br /><br />В примере 3 из § 22 было получено квадратное уравнение <br />х<sup>2</sup> - 92х + 960 = 0. <br />Мы решали его так:
| + | |
| - | </p><p><img src="/images/b/b7/14-06-44.jpg" _fck_mw_filename="14-06-44.jpg" alt="" /><br /><br />А теперь решим это квадратное уравнение по формуле (3), учитывая, что в данном случае b = - 92, т. е. 2k = - 92, k = - 46. <br />Имеем
| + | |
| - | </p><p><img src="/images/9/94/14-06-45.jpg" _fck_mw_filename="14-06-45.jpg" alt="" /><br /><br />Думается, что преимущества новой формулы вы оценили. <br />В заключение параграфа рассмотрим еще одно квадратное уравнение, которое мы решали по старой формуле (см. пример 6 из § 20), а теперь решим по-новому. Речь идет об уравнении
| + | |
| - | </p><p><img src="/images/2/2d/14-06-46.jpg" _fck_mw_filename="14-06-46.jpg" alt="" /><br /><br />Сравните этот вариант решения с тем, который был предложен в § 20. Согласитесь, что так работать проще. <br />Итак, если вам встретилось квадратное уравнение вида ах<sup>2</sup> + 2kx + с = 0, то советуем пользоваться формулой (2) (или (3), в случае, когда а = 1), поскольку вычисления будут проще. Но если вы опасаетесь запутаться в обилии формул, то пользуйтесь привычной общей формулой корней квадратного уравнения. <br /><br /><br />
| + | |
| - | </p><p><br />
| + | |
| - | </p><p><sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику <a href="Гипермаркет знаний - первый в мире!">онлайн</a>, курсы учителю по математике <a href="Математика">скачать</a></sub>
| + | |
| - | </p><p><br />
| + | |
| - | </p>
| + | |
| - | <pre class="_fck_mw_lspace"><b><u>Содержание урока</u></b>
| + | |
| - | <u></u><b><img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> конспект урока </b>
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> опорный каркас
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> презентация урока
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> акселеративные методы
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> интерактивные технологии
| + | |
| | | | |
| - | <b><u>Практика</u></b>
| + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Еще одна формула корней квадратного уравнения''' |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> задачи и упражнения
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> самопроверка
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> практикумы, тренинги, кейсы, квесты
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> домашние задания
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> дискуссионные вопросы
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> риторические вопросы от учеников
| + | |
| - |
| + | |
| - | <b><u>Иллюстрации</u></b>
| + | |
| - | <u></u><b><img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> аудио-, видеоклипы и мультимедиа </b>
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> фотографии, картинки
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> графики, таблицы, схемы
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> юмор, анекдоты, приколы, комиксы
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> притчи, поговорки, кроссворды, цитаты
| + | |
| | | | |
| - | <b><u>Дополнения</u></b> | + | <br> <br> |
| - | <u></u><b><img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> рефераты</b> | + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> статьи | + | '''Еще одна формула корней квадратного уравнения''' |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> фишки для любознательных
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> шпаргалки | + | <br>Мы с вами уже привыкли к тому, что '''[[Степени и корни. Степенные функции. Основные результаты|корни]]''' квадратного уравнения ах<sup>2</sup> + bх + с = 0 находятся по формуле |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> учебники основные и дополнительные | + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> словарь терминов | + | [[Image:14-06-37.jpg|320px|Формула]]<br><br>(если, конечно, дискриминант D = b<sup>2</sup> — 4ас — неотрицательное число; если же D < О, то приведенная формула не имеет смысла, а квадратное уравнение не имеет корней). |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> прочие
| + | |
| - | <b><u></u></b> | + | Но математики никогда не пройдут мимо возможности облегчить себе вычисления. Они обнаружили, что '''[[Конспект уроку на тему «Формула коренів квадратного рівняння»|формулу]]''' (1) можно упростить в случае, когда коэффициент b имеет вид b = 2k, в частности, если b есть четное число. <br>В самом деле, пусть у квадратного уравнения ах2 + Ьх + с = 0. |
| - | <u>Совершенствование учебников и уроков | + | |
| - | </u><b><img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> исправление ошибок в учебнике</b> | + | коэффициент b имеет вид b — 2k. Подставив в формулу (1) число 2k вместо b, получим: [[Image:14-06-38.jpg|480px|Решение]]<br><br>Итак, корни квадратного уравнения ах<sup>2</sup> + + 2kx + с = О можно вычислять по формуле |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> обновление фрагмента в учебнике
| + | |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> элементы новаторства на уроке
| + | [[Image:14-06-39.jpg|320px|Формула]]<br>Сравните эту формулу с формулой (1). В чем ее преимущества? |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> замена устаревших знаний новыми
| + | |
| | + | Во-первых, в квадрат возводится не число b, а его половина [[Image:14-06-40.jpg|Формула]] |
| | + | |
| | + | Во-вторых, вычитается из этого квадрата не 4ас, a просто ас. |
| | + | |
| | + | В-третьих, в знаменателе содержится не 2а, а просто а. Как видите, по крайней мере в трех моментах мы облегчаем себе выкладки. Особенно приятно выглядит формула (2) для приведенного '''[[Презентація уроку на тему "Квадратні рівняння. Теорема Вієта"|квадратного уравнения]]''', т. е. для случая, когда а = 1. Тогда получаем |
| | + | |
| | + | [[Image:14-06-41.jpg|320px|Формула]]<br><br>Это — формула корней уравнения х<sup>2</sup> + 2kx + с — 0. |
| | + | |
| | + | Вернемся к предыдущему параграфу и еще раз решим некоторые из имеющихся там квадратных уравнений — для сравнения трудоемкости вычислений по старой формуле (формуле (1)) и по новой формуле (формуле(2) или (3)). |
| | + | |
| | + | В примере 1 из § 22 получилось квадратное уравнение х<sup>2</sup> + 10x - 7200 = 0. |
| | + | |
| | + | Мы решали его так: |
| | + | |
| | + | [[Image:14-06-42.jpg|420px|Решение]]<br><br>А теперь решим то же квадратное уравнение по формуле (3), учитывая, что в данном случае b = 10, т. е. 2k = 10, k = 5. Имеем |
| | + | |
| | + | [[Image:14-06-43.jpg|420px|Решение]]<br><br>В примере 3 из § 22 было получено квадратное уравнение х<sup>2</sup> - 92х + 960 = 0. |
| | + | |
| | + | Мы решали его так: |
| | + | |
| | + | [[Image:14-06-44.jpg|320px|Решение]]<br><br>А теперь решим это квадратное уравнение по формуле (3), учитывая, что в данном случае b = - 92, т. е. 2k = - 92, k = - 46. |
| | + | |
| | + | Имеем |
| | + | |
| | + | [[Image:14-06-45.jpg|320px|Решение]]<br><br>Думается, что преимущества новой формулы вы оценили. |
| | + | |
| | + | В заключение параграфа рассмотрим еще одно квадратное уравнение, которое мы решали по старой формуле (см. пример 6 из § 20), а теперь решим по-новому. Речь идет об уравнении |
| | + | |
| | + | [[Image:14-06-46.jpg|420px|Решение]]<br><br>Сравните этот вариант решения с тем, который был предложен в § 20. Согласитесь, что так работать проще. <br>Итак, если вам встретилось квадратное уравнение вида ах<sup>2</sup> + 2kx + с = 0, то советуем пользоваться формулой (2) (или (3), в случае, когда а = 1), поскольку вычисления будут проще. Но если вы опасаетесь запутаться в обилии формул, то пользуйтесь привычной общей формулой корней квадратного уравнения. <br><br> |
| | + | |
| | + | ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' |
| | + | |
| | + | <br> |
| | + | |
| | + | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса [[Математика|скачать]]</sub> |
| | + | |
| | + | <br> |
| | + | |
| | + | '''<u>Содержание урока</u>''' |
| | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| - | <b><u>Только для учителей</u></b>
| + | '''<u>Практика</u>''' |
| - | <u></u><b><img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> идеальные уроки </b> | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> методические рекомендации
| + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | <img src="/images/9/95/1236084776_kr.jpg" _fck_mw_filename="1236084776 kr.jpg" _fck_mw_width="10" _fck_mw_height="10" alt="1236084776 kr.jpg" /> обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| | + | |
| | + | '''<u>Иллюстрации</u>''' |
| | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | + | |
| | + | '''<u>Дополнения</u>''' |
| | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | + | '''<u></u>''' |
| | + | <u>Совершенствование учебников и уроков |
| | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| | + | |
| | + | '''<u>Только для учителей</u>''' |
| | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | + | |
| | + | |
| | + | '''<u>Интегрированные уроки</u>'''<u> |
| | + | </u> |
| | + | |
| | + | <br> |
| | | | |
| | + | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. |
| | | | |
| - | <b><u>Интегрированные уроки</u></b><u>
| + | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. |
| - | </u>
| + | |
| - | </pre>
| + | |
| - | <p><br />
| + | |
| - | </p><p>Если у вас есть исправления или предложения к данному уроку, <a href="http://xvatit.com/index.php?do=feedback">напишите нам</a>.
| + | |
| - | </p><p>Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - <a href="http://xvatit.com/forum/">Образовательный форум</a>.
| + | |
| - | </p>
| + | |
Текущая версия на 12:47, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Еще одна формула корней квадратного уравнения
Еще одна формула корней квадратного уравнения
Мы с вами уже привыкли к тому, что корни квадратного уравнения ах2 + bх + с = 0 находятся по формуле

(если, конечно, дискриминант D = b2 — 4ас — неотрицательное число; если же D < О, то приведенная формула не имеет смысла, а квадратное уравнение не имеет корней).
Но математики никогда не пройдут мимо возможности облегчить себе вычисления. Они обнаружили, что формулу (1) можно упростить в случае, когда коэффициент b имеет вид b = 2k, в частности, если b есть четное число.
В самом деле, пусть у квадратного уравнения ах2 + Ьх + с = 0.
коэффициент b имеет вид b — 2k. Подставив в формулу (1) число 2k вместо b, получим: 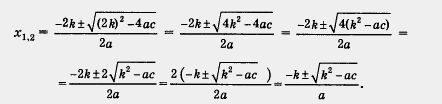
Итак, корни квадратного уравнения ах2 + + 2kx + с = О можно вычислять по формуле
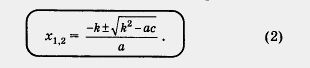
Сравните эту формулу с формулой (1). В чем ее преимущества?
Во-первых, в квадрат возводится не число b, а его половина 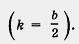
Во-вторых, вычитается из этого квадрата не 4ас, a просто ас.
В-третьих, в знаменателе содержится не 2а, а просто а. Как видите, по крайней мере в трех моментах мы облегчаем себе выкладки. Особенно приятно выглядит формула (2) для приведенного квадратного уравнения, т. е. для случая, когда а = 1. Тогда получаем

Это — формула корней уравнения х2 + 2kx + с — 0.
Вернемся к предыдущему параграфу и еще раз решим некоторые из имеющихся там квадратных уравнений — для сравнения трудоемкости вычислений по старой формуле (формуле (1)) и по новой формуле (формуле(2) или (3)).
В примере 1 из § 22 получилось квадратное уравнение х2 + 10x - 7200 = 0.
Мы решали его так:
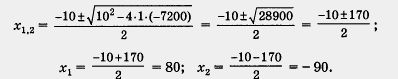
А теперь решим то же квадратное уравнение по формуле (3), учитывая, что в данном случае b = 10, т. е. 2k = 10, k = 5. Имеем
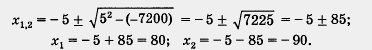
В примере 3 из § 22 было получено квадратное уравнение х2 - 92х + 960 = 0.
Мы решали его так:
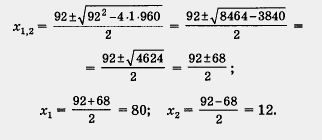
А теперь решим это квадратное уравнение по формуле (3), учитывая, что в данном случае b = - 92, т. е. 2k = - 92, k = - 46.
Имеем
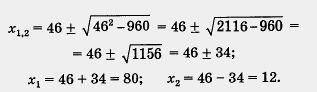
Думается, что преимущества новой формулы вы оценили.
В заключение параграфа рассмотрим еще одно квадратное уравнение, которое мы решали по старой формуле (см. пример 6 из § 20), а теперь решим по-новому. Речь идет об уравнении
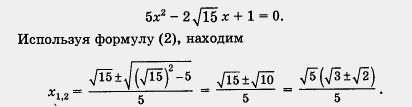
Сравните этот вариант решения с тем, который был предложен в § 20. Согласитесь, что так работать проще.
Итак, если вам встретилось квадратное уравнение вида ах2 + 2kx + с = 0, то советуем пользоваться формулой (2) (или (3), в случае, когда а = 1), поскольку вычисления будут проще. Но если вы опасаетесь запутаться в обилии формул, то пользуйтесь привычной общей формулой корней квадратного уравнения.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|