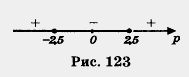|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Решение квадратных неравенств</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Решение квадратных неравенств, неравенство, луча, график, уравнения, корни, коэффициент, алгоритм, функции, числовая прямая, формулой, рациональных, Квадратное уравнение</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Решение квадратных неравенств''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Решение квадратных неравенств''' |
| | | | |
| - | <br> | + | <br> '''Решение квадратных неравенств''' |
| - | | + | |
| - | | + | |
| | | | |
| - | '''РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ '''
| + | <br>Квадратным неравенством называют '''[[Презентація до теми Розв'язування лінійних нерівностей|неравенство]]''' вида ах<sup>2</sup> + bх + 0 0, где [[Image:15-06-1.jpg]] (вместо знака > может быть, разумеется, любой другой знак неравенства). Всеми необходимыми для решения таких неравенств фактами теории мы с вами располагаем, в чем сейчас и убедимся. |
| | | | |
| - | <br>Квадратным неравенством называют неравенство вида ах<sup>2</sup> + bх + 0 0, где [[Image:15-06-1.jpg]] (вместо знака > может быть, разумеется, любой другой знак неравенства). Всеми необходимыми для решения таких неравенств фактами теории мы с вами располагаем, в чем сейчас и убедимся.
| + | '''Пример 1'''. Решить неравенство: |
| | | | |
| - | '''Пример 1'''. Решить неравенство: <br>а) х<sup>2</sup> - 2х - 3 >0; б) х<sup>2</sup> - 2х - 3 < 0; <br>в) х<sup>2</sup> - 2х - 3 > 0; г) х<sup>2</sup> - 2х - 3 < 0. <br>Решение,
| + | а) х<sup>2</sup> - 2х - 3 >0; б) х<sup>2</sup> - 2х - 3 < 0; <br>в) х<sup>2</sup> - 2х - 3 > 0; г) х<sup>2</sup> - 2х - 3 < 0. <br>Решение, |
| | | | |
| - | а) Рассмотрим параболу у = х<sup>2</sup> - 2х - 3, изображенную на рис. 117. | + | а) Рассмотрим параболу у = х<sup>2</sup> - 2х - 3, изображенную на рис. 117. |
| | | | |
| - | [[Image:15-06-2.jpg]] | + | [[Image:15-06-2.jpg|240px|Парабола]] |
| | | | |
| | Решить неравенство х<sup>2</sup> - 2х - 3 > 0 — это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны. | | Решить неравенство х<sup>2</sup> - 2х - 3 > 0 — это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны. |
| Строка 21: |
Строка 19: |
| | Замечаем, что у > 0, т. е. график функции расположен выше оси х, при х < -1 или при х > 3. | | Замечаем, что у > 0, т. е. график функции расположен выше оси х, при х < -1 или при х > 3. |
| | | | |
| - | Значит, решениями неравенства служат все точки открытого луча (-<sub>00</sub>, - 1), а также все точки открытого луча (3, <sub>+00</sub>). <br>Используя знак U (знак объединения множеств), ответ можно записать так: (<sub>—00</sub>, - 1) U (3, <sub>+00</sub>). Впрочем, ответ можно записать и так: х < - 1; х > 3. | + | Значит, решениями неравенства служат все точки открытого '''[[Плоскость. Прямая. Луч|луча]]''' (-<sub>00</sub>, - 1), а также все точки открытого луча (3, <sub>+00</sub>). |
| | | | |
| - | б) Неравенство х<sup>2</sup> - 2х - 3 < 0, или у < 0, где у = х<sup>2</sup> - 2х - 3, также можно решить с помощью рис. 117: график расположен ниже оси х, если -1 < х < 3. Поэтому решениями данного неравенства служат все точки интервала (— 1, 3). | + | Используя знак U (знак объединения множеств), ответ можно записать так: (<sub>—00</sub>, - 1) U (3, <sub>+00</sub>). Впрочем, ответ можно записать и так: х < - 1; х > 3. |
| | + | |
| | + | б) Неравенство х<sup>2</sup> - 2х - 3 < 0, или у < 0, где у = х<sup>2</sup> - 2х - 3, также можно решить с помощью рис. 117: '''[[Приклади графіків залежностей між величинами|график]]''' расположен ниже оси х, если -1 < х < 3. Поэтому решениями данного неравенства служат все точки интервала (— 1, 3). |
| | | | |
| | в) Неравенство х<sup>2</sup> - 2х - 3 > 0 отличается от неравенства х<sup>2</sup> - 2х - 3 > 0 тем, что в ответ надо включить и корни уравнения х<sup>2</sup> - 2х - 3 = 0, т. е. точки х = -1 | | в) Неравенство х<sup>2</sup> - 2х - 3 > 0 отличается от неравенства х<sup>2</sup> - 2х - 3 > 0 тем, что в ответ надо включить и корни уравнения х<sup>2</sup> - 2х - 3 = 0, т. е. точки х = -1 |
| Строка 29: |
Строка 29: |
| | и х = 3. Таким образом, решениями данного нестрогого неравенства являются все точки луча (<sub>-00</sub>, - 1], а также все точки луча [3, <sup>+00</sup>). | | и х = 3. Таким образом, решениями данного нестрогого неравенства являются все точки луча (<sub>-00</sub>, - 1], а также все точки луча [3, <sup>+00</sup>). |
| | | | |
| - | г) Неравенство х<sup>2</sup> - 2х - 3 < 0 отличается от неравенства х<sup>2</sup> - 2х - 3 < 0 тем, что в ответ надо включить и корни уравнения х<sup>2</sup> - 2х - 3 = 0, т. е. х = -1 и х = 3. Следовательно, решениями данного нестрогого неравенства служат все точки отрезка [-1, 3]. <br>Практичные математики обычно говорят так: зачем нам, решая неравенство ах<sup>2</sup> + bх + с > 0, аккуратно строить параболу график квадратичной функции | + | г) Неравенство х<sup>2</sup> - 2х - 3 < 0 отличается от неравенства х<sup>2</sup> - 2х - 3 < 0 тем, что в ответ надо включить и корни '''[[Розв'язування рівнянь. Презентація уроку|уравнения]]''' х<sup>2</sup> - 2х - 3 = 0, т. е. х = -1 и х = 3. Следовательно, решениями данного нестрогого неравенства служат все точки отрезка [-1, 3]. |
| | | | |
| - | у = ах<sup>2</sup> + bх + с (как это было сделано в примере 1)? Достаточно сделать схематический набросок графика, для чего следует лишь найти корни квадратного <br>трехчлена (точки пересечения параболы с осью х) и определить, куда направлены ветви параболы — вверх или вниз. Этот схематический набросок даст наглядное истолкование решению неравенства.
| + | Практичные математики обычно говорят так: зачем нам, решая неравенство ах<sup>2</sup> + bх + с > 0, аккуратно строить параболу график квадратичной функции |
| | | | |
| - | '''Пример 2.''' Решить неравенство - 2х<sup>2</sup> + Зх + 9 < 0. <br>Решение. | + | у = ах<sup>2</sup> + bх + с (как это было сделано в примере 1)? Достаточно сделать схематический набросок графика, для чего следует лишь найти '''[[Степени и корни. Степенные функции. Основные результаты|корни]]''' квадратного трехчлена (точки пересечения параболы с осью х) и определить, куда направлены ветви параболы — вверх или вниз. Этот схематический набросок даст наглядное истолкование решению неравенства. |
| | + | |
| | + | '''Пример 2.''' Решить неравенство - 2х<sup>2</sup> + Зх + 9 < 0. <br>Решение. |
| | | | |
| | 1) Найдем корни квадратного трехчлена - 2х<sup>2</sup> + Зх + 9: х<sub>1</sub> = 3; х<sub>2</sub> = - 1,5. | | 1) Найдем корни квадратного трехчлена - 2х<sup>2</sup> + Зх + 9: х<sub>1</sub> = 3; х<sub>2</sub> = - 1,5. |
| | | | |
| - | 2) Парабола, служащая графиком функции у = -2х<sup>2</sup> + Зх + 9, пересекает ось х в точках 3 и - 1,5, а ветви параболы направлены вниз, поскольку старший коэффициент — отрицательное число - 2. На рис. 118 представлен набросок графика. | + | 2) Парабола, служащая графиком функции у = -2х<sup>2</sup> + Зх + 9, пересекает ось х в точках 3 и - 1,5, а ветви параболы направлены вниз, поскольку старший '''[[Задачі: Переставна і сполучна властивості множення. Коефіцієнт|коэффициент]]''' — отрицательное число - 2. На рис. 118 представлен набросок графика. |
| | | | |
| - | [[Image:15-06-3.jpg]] | + | [[Image:15-06-3.jpg|240px|Парабола]] |
| | | | |
| - | 3) Используя рис. 118, делаем вывод: у < 0 на тех промежутках оси х, где график расположен ниже оси х, т.е. на открытом луче (-оо, -1,5) или на открытом луче C, +оо). <br>От вет: х < -1,5; х > 3. | + | 3) Используя рис. 118, делаем вывод: у < 0 на тех промежутках оси х, где график расположен ниже оси х, т.е. на открытом луче (-оо, -1,5) или на открытом луче C, +оо). <br>Ответ: х < -1,5; х > 3. |
| | | | |
| - | '''Пример 3.''' Решить неравенство 4х<sup>2</sup> - 4х + 1 < 0. <br>Решение. | + | '''Пример 3.''' Решить неравенство 4х<sup>2</sup> - 4х + 1 < 0. <br>Решение. |
| | | | |
| | 1) Из уравнения 4х<sup>2</sup> - 4х + 1 = 0 находим [[Image:15-06-4.jpg]]. <br><br>2) Квадратный трехчлен имеет один корень [[Image:15-06-5.jpg]]; это значит, что парабола, служащая графиком квадратного трехчлена, не пересекает ось х, а касается ее в точке [[Image:15-06-5.jpg]]. Ветви параболы направлены вверх (рис. 119.) | | 1) Из уравнения 4х<sup>2</sup> - 4х + 1 = 0 находим [[Image:15-06-4.jpg]]. <br><br>2) Квадратный трехчлен имеет один корень [[Image:15-06-5.jpg]]; это значит, что парабола, служащая графиком квадратного трехчлена, не пересекает ось х, а касается ее в точке [[Image:15-06-5.jpg]]. Ветви параболы направлены вверх (рис. 119.) |
| | | | |
| - | [[Image:15-06-6.jpg]]<br><br>3) С помощью геометрической модели, представленной на рис. 119, устанавливаем, что заданное неравенство выполняется только в точке [[Image:15-06-5.jpg]], поскольку при всех других значениях х ординаты графика положительны. <br>Ответ: [[Image:15-06-5.jpg]]. <br>Вы, наверное, заметили, что фактически в примерах 1, 2, 3 использовался вполне определенный алгоритм решения квадратных неравенств, оформим его. | + | [[Image:15-06-6.jpg|240px|Парабола]]<br><br>3) С помощью геометрической модели, представленной на рис. 119, устанавливаем, что заданное неравенство выполняется только в точке [[Image:15-06-5.jpg]], поскольку при всех других значениях х ординаты графика положительны. <br>Ответ: [[Image:15-06-5.jpg]]. <br>Вы, наверное, заметили, что фактически в примерах 1, 2, 3 использовался вполне определенный '''[[Урок 4. Программа действий. Алгоритм|алгоритм]]''' решения квадратных неравенств, оформим его. |
| | | | |
| - | <br>'''Алгоритм решения квадратного неравенства ах<sup>2</sup> + bх + 0 0 (ах<sup>2</sup> + bх + с < 0)''' | + | <br>'''Алгоритм решения квадратного неравенства ах<sup>2</sup> + bх + 0 0 (ах<sup>2</sup> + bх + с < 0)'''<br> |
| | | | |
| - | | + | [[Image:15-06-7.jpg|480px|Алгоритм решения квадратного неравенства]] |
| - | | + | |
| - | [[Image:15-06-7.jpg]] | + | |
| | | | |
| | <br>На первом шаге этого алгоритма требуется найти корни квадратного трехчлена. Но ведь корни могут и не существовать, что же делать? Тогда алгоритм неприменим, значит, надо рассуждать как-то по-другому. Ключ к этим рассуждениям дают следующие теоремы. | | <br>На первом шаге этого алгоритма требуется найти корни квадратного трехчлена. Но ведь корни могут и не существовать, что же делать? Тогда алгоритм неприменим, значит, надо рассуждать как-то по-другому. Ключ к этим рассуждениям дают следующие теоремы. |
| | | | |
| - | [[Image:15-06-8.jpg]]<br><br>Иными словами, если D < 0, а > 0, то неравенство ах<sup>2</sup> + bх + с > 0 выполняется при всех х; напротив, неравенство ах<sup>2</sup> + bх + с < 0 не имеет решений. <br>'''''Доказательство.''''' Графиком функции у = ах<sup>2</sup> + bх + с является парабола, ветви которой направлены вверх (поскольку а > 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 120. Видим, что при всех х график расположен выше оси х, а это значит, что при всех х выполняется неравенство ах<sup>2</sup> + bх + с > 0, что и требовалось доказать. | + | [[Image:15-06-8.jpg|480px|Теорема]]<br><br>Иными словами, если D < 0, а > 0, то неравенство ах<sup>2</sup> + bх + с > 0 выполняется при всех х; напротив, неравенство ах<sup>2</sup> + bх + с < 0 не имеет решений. <br>'''''Доказательство.''''' Графиком '''[[Предел функции|функции]]''' у = ах<sup>2</sup> + bх + с является парабола, ветви которой направлены вверх (поскольку а > 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 120. Видим, что при всех х график расположен выше оси х, а это значит, что при всех х выполняется неравенство ах<sup>2</sup> + bх + с > 0, что и требовалось доказать. |
| | | | |
| - | [[Image:15-06-9.jpg]] | + | [[Image:15-06-9.jpg|480px|Теорема]] |
| | | | |
| | Иными словами, если D < 0, а < 0, то неравенство ах<sup>2</sup> + bх + с < 0 выполняется при всех х; напротив, неравенство ах<sup>2</sup> + bх + с > 0 не имеет решений. | | Иными словами, если D < 0, а < 0, то неравенство ах<sup>2</sup> + bх + с < 0 выполняется при всех х; напротив, неравенство ах<sup>2</sup> + bх + с > 0 не имеет решений. |
| | | | |
| - | [[Image:15-06-10.jpg]]<br> <br>'''''Доказательство.''''' Графиком функции у = ах<sup>2</sup> + bх +с является парабола, ветви которой направлены вниз (поскольку а < 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 121. Видим, что при всех х график расположен ниже оси х, а это значит, что при всех х выполняется неравенство ах<sup>2</sup> + bх + с < 0, что и требовалось доказать. | + | [[Image:15-06-10.jpg|480px|Парабола]]<br> <br>'''''Доказательство.''''' Графиком функции у = ах<sup>2</sup> + bх +с является парабола, ветви которой направлены вниз (поскольку а < 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 121. Видим, что при всех х график расположен ниже оси х, а это значит, что при всех х выполняется неравенство ах<sup>2</sup> + bх + с < 0, что и требовалось доказать. |
| | | | |
| - | '''Пример 4'''. Решить неравенство: <br>а) 2х<sup>2</sup> - х + 4 >0; б) -х<sup>2</sup>+ Зх - 8 >0. <br>Решение, | + | '''Пример 4'''. Решить неравенство: |
| | | | |
| - | а) Найдем дискриминант квадратного трехчлена 2х<sup>2</sup> - х + 4. Имеем D = (-1)<sup>2</sup> - 4 • 2 • 4 = - 31 < 0. <br>Старший коэффициент трехчлена (число 2) положителен. <br>Значит, по теореме 1, при всех х выполняется неравенство 2x<sup>2</sup> - х + 4 > 0, т. е. решением заданного неравенства служит вся числовая прямая (<sub>-00</sub>, <sub>+ 00</sub>). | + | а) 2х<sup>2</sup> - х + 4 >0; б) -х<sup>2</sup>+ Зх - 8 >0. |
| | | | |
| - | б) Найдем дискриминант квадратного трехчлена - х<sup>2</sup> + Зх - 8. Имеем D = З2 - 4 • (- 1) • (- 8) = - 23 < 0. Старший коэффициент трехчлена (число - 1) отрицателен. Следовательно, по теореме 2, при всех х выполняется неравенство - х<sup>2</sup> + Зx - 8 < 0. Это значит, что неравенство — х<sup>2</sup> + Зх — 8 [[Image:15-06-11.jpg]] 0 не выполняется ни при каком значении х, т. е. заданное неравенство не имеет решений. <br>Ответ: а) (<sub>-00</sub>, <sub>+ 00</sub>); б) нет решений.
| + | Решение, |
| | | | |
| - | В следующем примере мы познакомимся еще с одним способом рассуждений, который применяется при решении квадратных неравенств.
| + | а) Найдем дискриминант квадратного трехчлена 2х<sup>2</sup> - х + 4. Имеем D = (-1)<sup>2</sup> - 4 • 2 • 4 = - 31 < 0. <br>Старший коэффициент трехчлена (число 2) положителен. |
| | | | |
| - | '''Пример 5.''' Решить неравенство Зх<sup>2</sup> - 10х + 3 < 0. <br>Решение. Разложим квадратный трехчлен Зx<sup>2</sup> - 10x + 3 на множители. Корнями трехчлена являются числа 3 и [[Image:15-06-12.jpg]], поэтому воспользовавшись формулой <br>ах<sup>2</sup> + bх + с = а (х - x<sub>1</sub>)(x - х<sub>2</sub>),
| + | Значит, по теореме 1, при всех х выполняется неравенство 2x<sup>2</sup> - х + 4 > 0, т. е. решением заданного неравенства служит вся '''[[Задачі на тему «Координатна пряма. Раціональні числа»|числовая прямая]]''' (<sub>-00</sub>, <sub>+ 00</sub>). |
| | | | |
| - | получим <br>Зx<sup>2</sup> - 10х + 3 = 3(х - 3) (х - [[Image:15-06-12.jpg]])<br>Отметим на числовой прямой корни трехчлена: 3 и [[Image:15-06-12.jpg]] (рис. 122).
| + | б) Найдем дискриминант квадратного трехчлена - х<sup>2</sup> + Зх - 8. Имеем D = З2 - 4 • (- 1) • (- 8) = - 23 < 0. Старший коэффициент трехчлена (число - 1) отрицателен. Следовательно, по теореме 2, при всех х выполняется неравенство - х<sup>2</sup> + Зx - 8 < 0. Это значит, что неравенство — х<sup>2</sup> + Зх — 8 [[Image:15-06-11.jpg]] 0 не выполняется ни при каком значении х, т. е. заданное неравенство не имеет решений. |
| | | | |
| - | [[Image:15-06-13.jpg]] | + | Ответ: а) (<sub>-00</sub>, <sub>+ 00</sub>); б) нет решений. |
| | + | |
| | + | В следующем примере мы познакомимся еще с одним способом рассуждений, который применяется при решении квадратных неравенств. |
| | + | |
| | + | '''Пример 5.''' Решить неравенство Зх<sup>2</sup> - 10х + 3 < 0. <br>Решение. Разложим квадратный трехчлен Зx<sup>2</sup> - 10x + 3 на множители. Корнями трехчлена являются числа 3 и [[Image:15-06-12.jpg]], поэтому воспользовавшись '''[[Конспект уроку на тему «Формула коренів квадратного рівняння»|формулой]]''' ах<sup>2</sup> + bх + с = а (х - x<sub>1</sub>)(x - х<sub>2</sub>),получим Зx<sup>2</sup> - 10х + 3 = 3(х - 3) (х - [[Image:15-06-12.jpg]])<br>Отметим на числовой прямой корни трехчлена: 3 и [[Image:15-06-12.jpg]] (рис. 122). |
| | + | |
| | + | [[Image:15-06-13.jpg|240px|Числовая прямая]] |
| | | | |
| | Пусть х > 3; тогда x-3>0 и x-[[Image:15-06-12.jpg]]>0, а значит, и произведение 3(х - 3)( х - [[Image:15-06-12.jpg]]) положительно. Далее, пусть [[Image:15-06-12.jpg]] < х < 3; тогда x-3< 0, а х-[[Image:15-06-12.jpg]] >0. Следовательно, произведение 3(х-3)(х-[[Image:15-06-12.jpg]]) отрицательно. Пусть, наконец, х <[[Image:15-06-12.jpg]]; тогда x-3< 0 и x-[[Image:15-06-12.jpg]] < 0. Но в таком случае произведение <br>3(x -3)( x -[[Image:15-06-12.jpg]]) положительно. | | Пусть х > 3; тогда x-3>0 и x-[[Image:15-06-12.jpg]]>0, а значит, и произведение 3(х - 3)( х - [[Image:15-06-12.jpg]]) положительно. Далее, пусть [[Image:15-06-12.jpg]] < х < 3; тогда x-3< 0, а х-[[Image:15-06-12.jpg]] >0. Следовательно, произведение 3(х-3)(х-[[Image:15-06-12.jpg]]) отрицательно. Пусть, наконец, х <[[Image:15-06-12.jpg]]; тогда x-3< 0 и x-[[Image:15-06-12.jpg]] < 0. Но в таком случае произведение <br>3(x -3)( x -[[Image:15-06-12.jpg]]) положительно. |
| Строка 83: |
Строка 89: |
| | Подводя итог рассуждениям, приходим к выводу: знаки квадратного трехчлена Зx<sup>2</sup> - 10х + 3 изменяются так, как показано на рис. 122. Нас же интересует, при каких х квадратный трехчлен принимает отрицательные значения. Из рис. 122 делаем вывод: квадратный трехчлен Зx<sup>2</sup> - 10х + 3 принимает отрицательные значения для любого значения х из интервала ([[Image:15-06-12.jpg]], 3)<br>Ответ ([[Image:15-06-12.jpg]], 3), или [[Image:15-06-12.jpg]] < х < 3. | | Подводя итог рассуждениям, приходим к выводу: знаки квадратного трехчлена Зx<sup>2</sup> - 10х + 3 изменяются так, как показано на рис. 122. Нас же интересует, при каких х квадратный трехчлен принимает отрицательные значения. Из рис. 122 делаем вывод: квадратный трехчлен Зx<sup>2</sup> - 10х + 3 принимает отрицательные значения для любого значения х из интервала ([[Image:15-06-12.jpg]], 3)<br>Ответ ([[Image:15-06-12.jpg]], 3), или [[Image:15-06-12.jpg]] < х < 3. |
| | | | |
| - | '''''Замечание.''''' Метод рассуждений, который мы применили в примере 5, обычно называют методом интервалов (или методом промежутков). Он активно используется в математике для решения рациональных неравенств. В 9-м классе мы изучим метод интервалов более детально. | + | '''''Замечание.''''' Метод рассуждений, который мы применили в примере 5, обычно называют методом интервалов (или методом промежутков). Он активно используется в математике для решения '''[[Преобразование рациональных выражений|рациональных]]''' неравенств. В 9-м классе мы изучим метод интервалов более детально. |
| | | | |
| | '''Пример 6'''. При каких значениях параметра р квадратное уравнение х<sup>2</sup> - 5х + р<sup>2</sup> = 0: <br>а) имеет два различных корня; | | '''Пример 6'''. При каких значениях параметра р квадратное уравнение х<sup>2</sup> - 5х + р<sup>2</sup> = 0: <br>а) имеет два различных корня; |
| | | | |
| - | б) имеет один корень; | + | б) имеет один корень; |
| | | | |
| | в) не имеет -корней? | | в) не имеет -корней? |
| | | | |
| - | Решение. Число корней квадратного уравнения <br>зависит от знака его дискриминанта D. В данном случае <br>находим D = 25 - 4р2. <br>а) Квадратное уравнение имеет два различных корня, если <br>?)>0, значит, задача сводится к решению неравенства <br>25 - 4р2 > 0. Умножим обе части этого неравенства на -1 (не <br>забыв изменить при этом знак неравенства). Получим равносиль- <br>ное неравенство 4р2 - 25 < 0. Далее имеем 4 (р - 2,5) (р + 2,5) < 0. <br>Знаки выражения 4(р - 2,5) (р + 2,5) указаны на рис. 123. <br>Делаем вывод, что неравенство 4{р - 2,5)(р + 2,5) < 0 выпол- <br>няется для всех значений р из <br>+ _ + интервала (-2,5; 2,5). Именно при <br>* *"р этих значениях параметра р данное <br>квадратное уравнение имеет два <br>различных корня. <br>-Z5 О Z5 <br>Рис. 123 <br>б) Квадратное уравнение имеет один корень, если D — 0. <br>Как мы установили выше, D = 0 при р = 2,5 или р = -2,5. <br>Именно при этих значениях параметра р данное квадратное <br>уравнение имеет только один корень. <br>в) Квадратное уравнение не имеет корней, если D < 0. Решим <br>неравенство 25 - 4р2 < 0. <br>Получаем 4р2 - 25 > 0; <br>4(р-2,5)(р + 2,5)>0, <br>откуда (см. рис. 123) р < -2,5; р > 2,5. При этих значениях <br>параметра р данное квадратное уравнение не имеет корней. <br>Ответ: а) при р е (-2,5, 2,5); <br>б) прир = 2,5 илир = -2,5; <br>в) при р < - 2,5 или р > 2,5. <br><br><br><br><br> | + | Решение. Число корней квадратного уравнения зависит от знака его дискриминанта D. В данном случае находим D = 25 - 4р<sup>2</sup>. |
| | | | |
| | + | а) Квадратное уравнение имеет два различных корня, если D>0, значит, задача сводится к решению неравенства 25 - 4р<sup>2</sup> > 0. Умножим обе части этого неравенства на -1 (не забыв изменить при этом знак неравенства). Получим равносильное неравенство 4р<sup>2</sup> - 25 < 0. Далее имеем 4 (р - 2,5) (р + 2,5) < 0. |
| | | | |
| | + | Знаки выражения 4(р - 2,5) (р + 2,5) указаны на рис. 123. |
| | | | |
| - | <sub>Помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 8 класса [[Математика|скачать]], календарно-тематическое планирование</sub>
| + | [[Image:15-06-14.jpg|240px|Знаки выражения]] |
| | + | |
| | + | Делаем вывод, что неравенство 4(р - 2,5)(р + 2,5) < 0 выполняется для всех значений р из интервала (-2,5; 2,5). Именно при этих значениях параметра р данное квадратное уравнение имеет два различных корня. |
| | + | |
| | + | б) '''[[Презентація уроку: Квадратні рівняння|квадратное уравнение]]''' имеет один корень, если D — 0. <br>Как мы установили выше, D = 0 при р = 2,5 или р = -2,5. |
| | + | |
| | + | Именно при этих значениях параметра р данное квадратное уравнение имеет только один корень. |
| | + | |
| | + | в) Квадратное уравнение не имеет корней, если D < 0. Решим неравенство 25 - 4р<sup>2</sup> < 0. |
| | + | |
| | + | Получаем 4р<sup>2</sup> - 25 > 0; 4 (р-2,5)(р + 2,5)>0, откуда (см. рис. 123) р < -2,5; р > 2,5. При этих значениях параметра р данное квадратное уравнение не имеет корней. |
| | + | |
| | + | Ответ: а) при р [[Image:15-06-15.jpg]] (-2,5, 2,5); |
| | + | |
| | + | б) при р = 2,5 илир = -2,5; <br> в) при р < - 2,5 или р > 2,5. <br><br>''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | | | |
| | <br> | | <br> |
| | + | |
| | + | <sub>Помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 8 класса [[Математика|скачать]], календарно-тематическое планирование</sub><br> |
| | + | |
| | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 19:07, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Решение квадратных неравенств
Решение квадратных неравенств
Квадратным неравенством называют неравенство вида ах2 + bх + 0 0, где 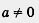 (вместо знака > может быть, разумеется, любой другой знак неравенства). Всеми необходимыми для решения таких неравенств фактами теории мы с вами располагаем, в чем сейчас и убедимся. (вместо знака > может быть, разумеется, любой другой знак неравенства). Всеми необходимыми для решения таких неравенств фактами теории мы с вами располагаем, в чем сейчас и убедимся.
Пример 1. Решить неравенство:
а) х2 - 2х - 3 >0; б) х2 - 2х - 3 < 0;
в) х2 - 2х - 3 > 0; г) х2 - 2х - 3 < 0.
Решение,
а) Рассмотрим параболу у = х2 - 2х - 3, изображенную на рис. 117.
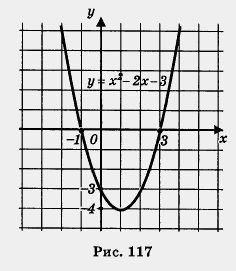
Решить неравенство х2 - 2х - 3 > 0 — это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны.
Замечаем, что у > 0, т. е. график функции расположен выше оси х, при х < -1 или при х > 3.
Значит, решениями неравенства служат все точки открытого луча (-00, - 1), а также все точки открытого луча (3, +00).
Используя знак U (знак объединения множеств), ответ можно записать так: (—00, - 1) U (3, +00). Впрочем, ответ можно записать и так: х < - 1; х > 3.
б) Неравенство х2 - 2х - 3 < 0, или у < 0, где у = х2 - 2х - 3, также можно решить с помощью рис. 117: график расположен ниже оси х, если -1 < х < 3. Поэтому решениями данного неравенства служат все точки интервала (— 1, 3).
в) Неравенство х2 - 2х - 3 > 0 отличается от неравенства х2 - 2х - 3 > 0 тем, что в ответ надо включить и корни уравнения х2 - 2х - 3 = 0, т. е. точки х = -1
и х = 3. Таким образом, решениями данного нестрогого неравенства являются все точки луча (-00, - 1], а также все точки луча [3, +00).
г) Неравенство х2 - 2х - 3 < 0 отличается от неравенства х2 - 2х - 3 < 0 тем, что в ответ надо включить и корни уравнения х2 - 2х - 3 = 0, т. е. х = -1 и х = 3. Следовательно, решениями данного нестрогого неравенства служат все точки отрезка [-1, 3].
Практичные математики обычно говорят так: зачем нам, решая неравенство ах2 + bх + с > 0, аккуратно строить параболу график квадратичной функции
у = ах2 + bх + с (как это было сделано в примере 1)? Достаточно сделать схематический набросок графика, для чего следует лишь найти корни квадратного трехчлена (точки пересечения параболы с осью х) и определить, куда направлены ветви параболы — вверх или вниз. Этот схематический набросок даст наглядное истолкование решению неравенства.
Пример 2. Решить неравенство - 2х2 + Зх + 9 < 0.
Решение.
1) Найдем корни квадратного трехчлена - 2х2 + Зх + 9: х1 = 3; х2 = - 1,5.
2) Парабола, служащая графиком функции у = -2х2 + Зх + 9, пересекает ось х в точках 3 и - 1,5, а ветви параболы направлены вниз, поскольку старший коэффициент — отрицательное число - 2. На рис. 118 представлен набросок графика.
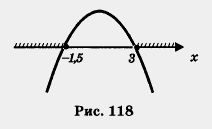
3) Используя рис. 118, делаем вывод: у < 0 на тех промежутках оси х, где график расположен ниже оси х, т.е. на открытом луче (-оо, -1,5) или на открытом луче C, +оо).
Ответ: х < -1,5; х > 3.
Пример 3. Решить неравенство 4х2 - 4х + 1 < 0.
Решение.
1) Из уравнения 4х2 - 4х + 1 = 0 находим 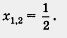 . .
2) Квадратный трехчлен имеет один корень 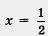 ; это значит, что парабола, служащая графиком квадратного трехчлена, не пересекает ось х, а касается ее в точке ; это значит, что парабола, служащая графиком квадратного трехчлена, не пересекает ось х, а касается ее в точке 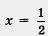 . Ветви параболы направлены вверх (рис. 119.) . Ветви параболы направлены вверх (рис. 119.)
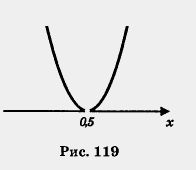
3) С помощью геометрической модели, представленной на рис. 119, устанавливаем, что заданное неравенство выполняется только в точке 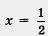 , поскольку при всех других значениях х ординаты графика положительны. , поскольку при всех других значениях х ординаты графика положительны.
Ответ: 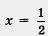 . .
Вы, наверное, заметили, что фактически в примерах 1, 2, 3 использовался вполне определенный алгоритм решения квадратных неравенств, оформим его.
Алгоритм решения квадратного неравенства ах2 + bх + 0 0 (ах2 + bх + с < 0)

На первом шаге этого алгоритма требуется найти корни квадратного трехчлена. Но ведь корни могут и не существовать, что же делать? Тогда алгоритм неприменим, значит, надо рассуждать как-то по-другому. Ключ к этим рассуждениям дают следующие теоремы.

Иными словами, если D < 0, а > 0, то неравенство ах2 + bх + с > 0 выполняется при всех х; напротив, неравенство ах2 + bх + с < 0 не имеет решений.
Доказательство. Графиком функции у = ах2 + bх + с является парабола, ветви которой направлены вверх (поскольку а > 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 120. Видим, что при всех х график расположен выше оси х, а это значит, что при всех х выполняется неравенство ах2 + bх + с > 0, что и требовалось доказать.

Иными словами, если D < 0, а < 0, то неравенство ах2 + bх + с < 0 выполняется при всех х; напротив, неравенство ах2 + bх + с > 0 не имеет решений.
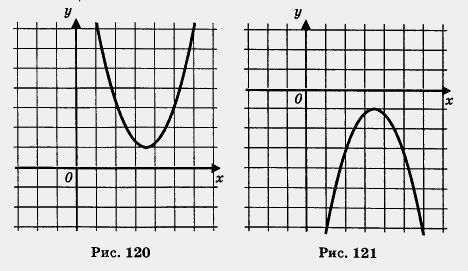
Доказательство. Графиком функции у = ах2 + bх +с является парабола, ветви которой направлены вниз (поскольку а < 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 121. Видим, что при всех х график расположен ниже оси х, а это значит, что при всех х выполняется неравенство ах2 + bх + с < 0, что и требовалось доказать.
Пример 4. Решить неравенство:
а) 2х2 - х + 4 >0; б) -х2+ Зх - 8 >0.
Решение,
а) Найдем дискриминант квадратного трехчлена 2х2 - х + 4. Имеем D = (-1)2 - 4 • 2 • 4 = - 31 < 0.
Старший коэффициент трехчлена (число 2) положителен.
Значит, по теореме 1, при всех х выполняется неравенство 2x2 - х + 4 > 0, т. е. решением заданного неравенства служит вся числовая прямая (-00, + 00).
б) Найдем дискриминант квадратного трехчлена - х2 + Зх - 8. Имеем D = З2 - 4 • (- 1) • (- 8) = - 23 < 0. Старший коэффициент трехчлена (число - 1) отрицателен. Следовательно, по теореме 2, при всех х выполняется неравенство - х2 + Зx - 8 < 0. Это значит, что неравенство — х2 + Зх — 8 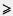 0 не выполняется ни при каком значении х, т. е. заданное неравенство не имеет решений. 0 не выполняется ни при каком значении х, т. е. заданное неравенство не имеет решений.
Ответ: а) (-00, + 00); б) нет решений.
В следующем примере мы познакомимся еще с одним способом рассуждений, который применяется при решении квадратных неравенств.
Пример 5. Решить неравенство Зх2 - 10х + 3 < 0.
Решение. Разложим квадратный трехчлен Зx2 - 10x + 3 на множители. Корнями трехчлена являются числа 3 и 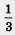 , поэтому воспользовавшись формулой ах2 + bх + с = а (х - x1)(x - х2),получим Зx2 - 10х + 3 = 3(х - 3) (х - , поэтому воспользовавшись формулой ах2 + bх + с = а (х - x1)(x - х2),получим Зx2 - 10х + 3 = 3(х - 3) (х - 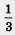 ) )
Отметим на числовой прямой корни трехчлена: 3 и 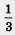 (рис. 122). (рис. 122).
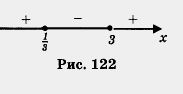
Пусть х > 3; тогда x-3>0 и x-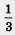 >0, а значит, и произведение 3(х - 3)( х - >0, а значит, и произведение 3(х - 3)( х - 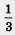 ) положительно. Далее, пусть ) положительно. Далее, пусть 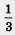 < х < 3; тогда x-3< 0, а х- < х < 3; тогда x-3< 0, а х-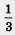 >0. Следовательно, произведение 3(х-3)(х- >0. Следовательно, произведение 3(х-3)(х-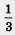 ) отрицательно. Пусть, наконец, х < ) отрицательно. Пусть, наконец, х <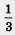 ; тогда x-3< 0 и x- ; тогда x-3< 0 и x-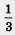 < 0. Но в таком случае произведение < 0. Но в таком случае произведение
3(x -3)( x -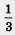 ) положительно. ) положительно.
Подводя итог рассуждениям, приходим к выводу: знаки квадратного трехчлена Зx2 - 10х + 3 изменяются так, как показано на рис. 122. Нас же интересует, при каких х квадратный трехчлен принимает отрицательные значения. Из рис. 122 делаем вывод: квадратный трехчлен Зx2 - 10х + 3 принимает отрицательные значения для любого значения х из интервала (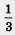 , 3) , 3)
Ответ (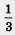 , 3), или , 3), или 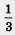 < х < 3. < х < 3.
Замечание. Метод рассуждений, который мы применили в примере 5, обычно называют методом интервалов (или методом промежутков). Он активно используется в математике для решения рациональных неравенств. В 9-м классе мы изучим метод интервалов более детально.
Пример 6. При каких значениях параметра р квадратное уравнение х2 - 5х + р2 = 0:
а) имеет два различных корня;
б) имеет один корень;
в) не имеет -корней?
Решение. Число корней квадратного уравнения зависит от знака его дискриминанта D. В данном случае находим D = 25 - 4р2.
а) Квадратное уравнение имеет два различных корня, если D>0, значит, задача сводится к решению неравенства 25 - 4р2 > 0. Умножим обе части этого неравенства на -1 (не забыв изменить при этом знак неравенства). Получим равносильное неравенство 4р2 - 25 < 0. Далее имеем 4 (р - 2,5) (р + 2,5) < 0.
Знаки выражения 4(р - 2,5) (р + 2,5) указаны на рис. 123.
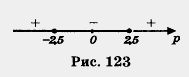
Делаем вывод, что неравенство 4(р - 2,5)(р + 2,5) < 0 выполняется для всех значений р из интервала (-2,5; 2,5). Именно при этих значениях параметра р данное квадратное уравнение имеет два различных корня.
б) квадратное уравнение имеет один корень, если D — 0.
Как мы установили выше, D = 0 при р = 2,5 или р = -2,5.
Именно при этих значениях параметра р данное квадратное уравнение имеет только один корень.
в) Квадратное уравнение не имеет корней, если D < 0. Решим неравенство 25 - 4р2 < 0.
Получаем 4р2 - 25 > 0; 4 (р-2,5)(р + 2,5)>0, откуда (см. рис. 123) р < -2,5; р > 2,5. При этих значениях параметра р данное квадратное уравнение не имеет корней.
Ответ: а) при р 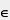 (-2,5, 2,5); (-2,5, 2,5);
б) при р = 2,5 илир = -2,5;
в) при р < - 2,5 или р > 2,5.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Помощь школьнику онлайн, Математика для 8 класса скачать, календарно-тематическое планирование
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|