|
|
| (1 промежуточная версия не показана) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Трапеция</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Трапеция, четырехугольник, признаку равенства, Теорема</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Трапеция''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Трапеция''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ТРАПЕЦИЯ''' | + | '''Трапеция''' |
| | | | |
| - | <br>'''''Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.''''' | + | <br>Трапецией называется '''[[Чотирикутник i його елементи|четырехугольник]]''', у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами. |
| | | | |
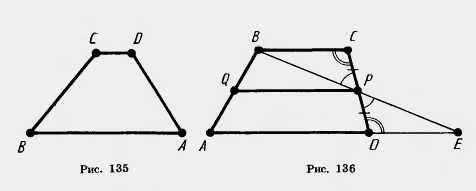
| - | На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD. | + | На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD. |
| | | | |
| - | '''''Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.''''' | + | '''[[Трапеція та її властивості. Середня лінія трапеції|Трапеция]]''', у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.<br> |
| | | | |
| | + | [[Image:22-06-16.jpg|480px|Трапеция]]<br><br>'''Теорема 6.8.''' Средняя линия трапеции параллельна основаниям и равна их полусумме. |
| | | | |
| | + | Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е. |
| | | | |
| - | [[Image:22-06-16.jpg]]<br><br>Теорема 6.8. '''''Средняя линия трапеции параллельна основаниям и равна их полусумме.''''' | + | Треугольники РВС и PED равны по второму '''[[Второй признак равенства треугольников. Полные уроки|признаку равенства]]''' треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED. |
| | | | |
| - | Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.
| + | Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок |
| | | | |
| - | Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED.
| + | [[Image:22-06-17.jpg|240px|Теорема доказана]]<br><br>'''[[Теоремы и доказательства. Полные уроки|Теорема]]''' доказана. |
| | | | |
| - | Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок
| + | Задача (60). Докажите, что у равнобокой трапеции углы при основании равны. |
| | | | |
| - | [[Image:22-06-17.jpg]]<br><br>Теорема доказана. | + | Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.<br><br>[[Image:22-06-18.jpg|320px|Трапеция]]<br> <br>Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и '''[[Трапеція та її властивості. Середня лінія трапеції|трапеции]]''' при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому [[Image:20-06-61.jpg]]ADC= [[Image:20-06-61.jpg]]BCD. Утверждение доказано. |
| | | | |
| - | Задача (60). Докажите, что у равнобокой трапеции углы при основании равны.
| + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ '''Геометрия'''] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.<br><br>[[Image:22-06-18.jpg]]<br> <br>Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому [[Image:20-06-61.jpg]]ADC= [[Image:20-06-61.jpg]]BCD. Утверждение доказано.<br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| - | <sub>Видео по математике[[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | <sub>Видео по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD.
Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.
Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок
Задача (60). Докажите, что у равнобокой трапеции углы при основании равны.
Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.
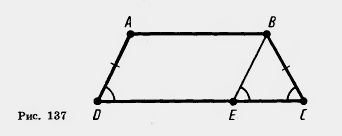
Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому  ADC=
ADC=  BCD. Утверждение доказано.
BCD. Утверждение доказано.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.