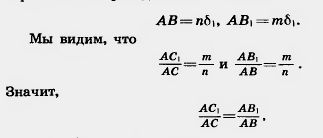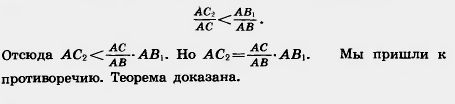|
|
| (3 промежуточные версии не показаны) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Теорема о пропорциональных отрезках</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Теорема о пропорциональных отрезках, Параллельные прямые, отрезок, теореме Фалеса, точку</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Теорема о пропорциональных отрезках''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Теорема о пропорциональных отрезках''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ'''<br>
| + | '''Теорема о пропорциональных отрезках'''<br> |
| | | | |
| - | <br>Теорема 6.9. '''''Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.''''' | + | <br>'''Теорема 6.9'''. '''[[Параллельные прямые. Полные уроки|Параллельные прямые]]''', пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. |
| | | | |
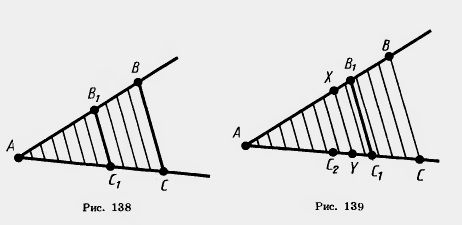
| - | Доказательство. Пусть стороны угла А пересекаются параллельными прямыми в точках В, С и B<sub>1</sub>,С<sub>1</sub> соответственно (рис. 138). Теоремой утверждается, что<br> | + | '''Доказательство'''. Пусть стороны угла А пересекаются параллельными прямыми в точках В, С и B<sub>1</sub>,С<sub>1</sub> соответственно (рис. 138). Теоремой утверждается, что<br> |
| | | | |
| - | [[Image:22-06-19.jpg]]<br><br>Докажем сначала равенство (*) в случае, когда существует такой отрезок длины [[Image:22-06-20.jpg]], который укладывается целое число раз и на отрезке АС, и на отрезке AС<sub>1</sub>. Пусть АС=n[[Image:22-06-20.jpg]], АС<sub>1</sub> = m[[Image:22-06-20.jpg]] и n>m. Разобьем отрезок АС на n равных частей (длины [[Image:22-06-20.jpg]]). При ЭТОМ точка С<sub>1</sub> будет одной из точек деления. | + | [[Image:22-06-19.jpg|240px|Доказательство]] |
| | | | |
| - | Проведем через точки деления прямые, параллельные прямой ВС. По теореме Фалеса эти прямые разбивают отрезок АВ на равные отрезки некоторой <br>
| + | <br>Докажем сначала равенство (*) в случае, когда существует такой '''[[Отрезок. Полные уроки|отрезок]]''' длины [[Image:22-06-20.jpg]], который укладывается целое число раз и на отрезке АС, и на отрезке AС<sub>1</sub>. Пусть АС=n[[Image:22-06-20.jpg]], АС<sub>1</sub> = m[[Image:22-06-20.jpg]] и n>m. Разобьем отрезок АС на n равных частей (длины [[Image:22-06-20.jpg]]). При этом точка С<sub>1</sub> будет одной из точек деления. |
| | | | |
| - | длины [[Image:22-06-20.jpg]]<sub>1</sub>). Имеем:<br> | + | Проведем через точки деления прямые, параллельные прямой ВС. По '''[[Теорема Фалеса. Середня лінія трикутника та її властивості|теореме Фалеса]]''' эти прямые разбивают отрезок АВ на равные отрезки некоторой длины [[Image:22-06-20.jpg]]<sub>1</sub>). Имеем:<br> |
| | | | |
| - | [[Image:22-06-21.jpg]]<br><br>что и требовалось доказать.<br>Докажем теорему в общем случае (не для запоминания). Допустим, что | + | [[Image:22-06-21.jpg|320px|Доказательство]]<br><br>что и требовалось доказать. |
| | | | |
| - | [[Image:22-06-22.jpg]]<br><br>[[Image:22-06-23.jpg]]<br>
| + | Докажем теорему в общем случае (не для запоминания). Допустим, что |
| | | | |
| - | Отложим на луче АС отрезок [[Image:22-06-24.jpg]]<br>При этом АС<sub>2</sub><АС<sub>1</sub>. Разобьем отрезок АС на большое число n равных частей и проведем через точки деления прямые, параллельные ВС.
| + | [[Image:22-06-22.jpg|240px|Доказательство]]<br><br>[[Image:22-06-27.jpg|480px|Теорема о пропорциональных отрезках]]<br> |
| | | | |
| - | При достаточно большом n на отрезке С<sub>1</sub>С2 будут точки деления. Обозначим одну из них через У, а соответствующую точку на отрезке АВ<sub>1</sub>, через X. По доказанному
| + | Отложим на луче АС отрезок [[Image:22-06-28.jpg|80px|Доказательство]]<br>При этом АС<sub>2</sub><АС<sub>1</sub>. Разобьем отрезок АС на большое число n равных частей и проведем через точки деления прямые, параллельные ВС. |
| | | | |
| - | [[Image:22-06-25.jpg]]<br><br>Заменим в этом равенстве величину AY меньшей величиной AС<sub>2</sub>, а величину АХ большей величиной АВ<sub>1</sub>. Получим:
| + | При достаточно большом n на отрезке С<sub>1</sub>С2 будут точки деления. Обозначим одну из них через У, а соответствующую '''[[Точки і прямі, їх властивості. Закриті вправи|точку]]''' на отрезке АВ<sub>1</sub>, через X. По доказанному |
| | | | |
| | + | [[Image:22-06-25.jpg|80px|Доказательство]]<br><br>Заменим в этом равенстве величину AY меньшей величиной AС<sub>2</sub>, а величину АХ большей величиной АВ<sub>1</sub>. Получим:<br> |
| | | | |
| | + | [[Image:22-06-26.jpg|480px|Доказательство]]<br> |
| | | | |
| - | [[Image:22-06-26.jpg]] | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ '''Геометрия'''] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 40: |
Строка 40: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Докажем теорему в общем случае (не для запоминания). Допустим, что
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.