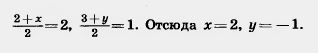|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Координаты середины отрезка</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Координаты середины отрезка, координаты, отрезка, формула, пересечения</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Координаты середины отрезка''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Координаты середины отрезка''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА'''
| + | '''Координаты середины отрезка''' |
| | | | |
| - | <br>Пусть А(Х<sub>1</sub>; у<sub>1</sub>) и В(х<sub>2</sub>; у<sub>2</sub>) — две произвольные точки и С (х; у) — середина отрезка АВ. Найдем координаты х, у точки С. | + | <br>Пусть А(Х<sub>1</sub>; у<sub>1</sub>) и В(х<sub>2</sub>; у<sub>2</sub>) — две произвольные точки и С (х; у) — середина отрезка АВ. Найдем [[Шкалы и координаты|координаты]] х, у точки С. |
| | | | |
| - | Рассмотрим сначала случай, когда отрезок АВ не параллелен оси у, т. е. Х<sub>1</sub>[[Image:22-06-97.jpg]]Х<sub>2</sub>. Проведем через точки А, В, С прямые, параллельные оси у (рис. 173). Они пересекут ось х в точках A<sub>1</sub>(X<sub>1</sub>; 0), B<sub>1</sub> (X<sub>2</sub>; 0), C<sub>1</sub>(х; 0). По теореме Фалеса точка С<sub>1</sub> будет серединой отрезка A<sub>1</sub>B<sub>1</sub>. | + | Рассмотрим сначала случай, когда отрезок АВ не параллелен оси у, т. е. Х<sub>1</sub>[[Image:22-06-97.jpg]]Х<sub>2</sub>. Проведем через точки А, В, С прямые, параллельные оси у (рис. 173). Они пересекут ось х в точках A<sub>1</sub>(X<sub>1</sub>; 0), B<sub>1</sub> (X<sub>2</sub>; 0), C<sub>1</sub>(х; 0). По теореме Фалеса точка С<sub>1</sub> будет серединой отрезка A<sub>1</sub>B<sub>1</sub>.<br> |
| | | | |
| | + | [[Image:22-06-99.jpg|240px|Координаты середины отрезка]]<br> |
| | | | |
| | + | Так как точка С<sub>1</sub> —середина [[Измерение отрезков. Полные уроки|отрезка]] AiBi, то A<sub>1</sub>C<sub>1</sub>=B<sub>1</sub>C<sub>1</sub>, а значит, Ix — X<sub>1</sub>I = Iх — Х<sub>2</sub>I. Отсюда следует, что либо x —x<sub>1</sub> = x — x<sub>2</sub>, либо (x — x<sub>1</sub>) = —(x-x<sub>2</sub>).<br> |
| | | | |
| - | [[Image:22-06-99.jpg]] | + | Первое равенство невозможно, так как x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub>. Поэтому верно второе. А из него получается [[Конспект уроку на тему «Формула коренів квадратного рівняння»|формула]] |
| | | | |
| | + | [[Image:22-06-98.jpg|100px|Формула ]]<br><br>Если x<sub>1</sub>=x<sub>2</sub>, т. е. отрезок АВ параллелен оси у, то все три точки A<sub>1</sub>, B<sub>1</sub>, C<sub>1</sub> имеют одну и ту же абсциссу. Значит, формула остается верной и в этом случае.<br> |
| | | | |
| | + | Ордината точки С находится аналогично. Через точки А, В, С проводятся прямые, параллельные оси х. <br> |
| | | | |
| - | Так как точка С<sub>1</sub> —середина отрезка AiBi, то A<sub>1</sub>C<sub>1</sub>=B<sub>1</sub>C<sub>1</sub>, а значит, Ix — X<sub>1</sub>I = Iх — Х<sub>2</sub>I. Отсюда следует, что либо x —x<sub>1</sub> = x — x<sub>2</sub>, либо (x — x<sub>1</sub>) = —(x-x<sub>2</sub>).<br>Первое равенство невозможно, так как x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub>. Поэтому верно второе. А из него получается формула
| + | Получается формула |
| | | | |
| - | [[Image:22-06-98.jpg]]<br><br>Если x<sub>1</sub>=x<sub>2</sub>, т. е. отрезок АВ параллелен оси у, то все три точки A<sub>1</sub>, B<sub>1</sub>, C<sub>1</sub> имеют одну и ту же абсциссу. Значит, формула остается верной и в этом случае.<br>Ордината точки С находится аналогично. Через точки А, В, С проводятся прямые, параллельные оси х. Получается формула | + | [[Image:22-06-100.jpg|100px|Формула ]]<br><br>'''Задача (15).''' Даны три вершины параллелограмма ABCD: А (1; 0), В (2; 3), С (3; 2). Найдите координаты четвертой вершины D и точки пересечения диагоналей. |
| | | | |
| - | [[Image:22-06-100.jpg]]<br><br>Задача (15). Даны три вершины параллелограмма ABCD: А (1; 0), В (2; 3), С (3; 2). Найдите координаты четвертой вершины D и точки пересечения диагоналей.
| + | '''Решение'''. Точка пересечения диагоналей является серединой каждой из них. Поэтому она является серединой отрезка АС, a значит, имеет координаты |
| | | | |
| - | Решение. Точка пересечения диагоналей является серединой каждой из них. Поэтому она является серединой отрезка АС, a значит, имеет координаты | + | [[Image:22-06-101.jpg|240px|Решение]]<br> <br>Теперь, зная координаты точки пересечения диагоналей, находим координаты х, у четвертой вершины D. Пользуясь тем, что точка [[Урок 39. Пересечение геометрических фигур|пересечения]] диагоналей является серединой отрезка BD, имеем: |
| | | | |
| - | [[Image:22-06-101.jpg]]<br> <br>Теперь, зная координаты точки пересечения диагоналей, находим координаты х, у четвертой вершины D. Пользуясь тем, что точка пересечения диагоналей является серединой отрезка BD, имеем: | + | [[Image:22-06-102.jpg|320px|Решение]]<br> |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [[Image:22-06-102.jpg]]<br><br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> | | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> |
| Строка 36: |
Строка 40: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 11:41, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Координаты середины отрезка
Координаты середины отрезка
Пусть А(Х1; у1) и В(х2; у2) — две произвольные точки и С (х; у) — середина отрезка АВ. Найдем координаты х, у точки С.
Рассмотрим сначала случай, когда отрезок АВ не параллелен оси у, т. е. Х1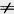 Х2. Проведем через точки А, В, С прямые, параллельные оси у (рис. 173). Они пересекут ось х в точках A1(X1; 0), B1 (X2; 0), C1(х; 0). По теореме Фалеса точка С1 будет серединой отрезка A1B1. Х2. Проведем через точки А, В, С прямые, параллельные оси у (рис. 173). Они пересекут ось х в точках A1(X1; 0), B1 (X2; 0), C1(х; 0). По теореме Фалеса точка С1 будет серединой отрезка A1B1.
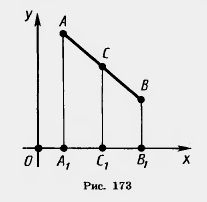
Так как точка С1 —середина отрезка AiBi, то A1C1=B1C1, а значит, Ix — X1I = Iх — Х2I. Отсюда следует, что либо x —x1 = x — x2, либо (x — x1) = —(x-x2).
Первое равенство невозможно, так как x1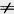 x2. Поэтому верно второе. А из него получается формула x2. Поэтому верно второе. А из него получается формула
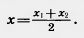
Если x1=x2, т. е. отрезок АВ параллелен оси у, то все три точки A1, B1, C1 имеют одну и ту же абсциссу. Значит, формула остается верной и в этом случае.
Ордината точки С находится аналогично. Через точки А, В, С проводятся прямые, параллельные оси х.
Получается формула
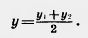
Задача (15). Даны три вершины параллелограмма ABCD: А (1; 0), В (2; 3), С (3; 2). Найдите координаты четвертой вершины D и точки пересечения диагоналей.
Решение. Точка пересечения диагоналей является серединой каждой из них. Поэтому она является серединой отрезка АС, a значит, имеет координаты
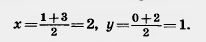
Теперь, зная координаты точки пересечения диагоналей, находим координаты х, у четвертой вершины D. Пользуясь тем, что точка пересечения диагоналей является серединой отрезка BD, имеем:
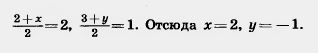
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|