|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Равенство векторов</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Равенство векторов, абсолютной величине, параллельному переносу</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Равенство векторов''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Равенство векторов''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' РАВЕНСТВО ВЕКТОРОВ'''<br> | + | '''Равенство векторов'''<br> |
| | | | |
| - | <br>'''''Два вектора называются равными, если они совмещаются параллельным переносом'''''. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. | + | <br>Два [[Презентація уроку: Означення вектора. Модуль і напрям вектора.Рівні вектори|вектора]] называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. |
| | | | |
| - | Из данного определения равенства векторов следует, что '''''равные векторы одинаково направлены и равны по абсолютной величине.'''''<br> | + | Из данного определения равенства векторов следует, что равные векторы одинаково направлены и равны по абсолютной величине.<br> |
| | | | |
| - | Обратно: '''''если векторы одинаково направлены и равны по абсолютной величине, то они равны.'''''<br> | + | Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.<br> |
| | | | |
| - | Действительно, пусть [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] — одинаково направленные векторы, равные по абсолютной величине (рис. 213). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую CD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, т. е. параллельный перенос переводит вектор [[Image:23-06-5.jpg]] в вектор [[Image:23-06-3.jpg]]. Значит, векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] равны, что и требовалось доказать.<br> <br>[[Image:23-06-9.jpg]]<br><br>Задача (2). Четырехугольник ABCD — параллелограмм. Докажите равенство векторов [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]].<br>Решение. Подвергнем вектор [[Image:23-06-3.jpg]] параллельному переносу, при котором точка А переходит в точку D (рис. 214). При этом переносе точка А смещается по прямой AD, а значит, точка В смещается по параллельной прямой ВС. Прямая АВ переходит в параллельную прямую, а значит, в прямую DC. | + | Действительно, пусть [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] — одинаково направленные векторы, равные по [[Абсолютная величина и направление вектора|абсолютной величине]] (рис. 213). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую CD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, т. е. параллельный перенос переводит вектор [[Image:23-06-5.jpg]] в вектор [[Image:23-06-3.jpg]]. Значит, векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] равны, что и требовалось доказать. <br>[[Image:23-06-9.jpg|480px|Равенство векторов]]<br><br>Задача (2). Четырехугольник ABCD — параллелограмм. Докажите равенство векторов [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]].<br>Решение. Подвергнем вектор [[Image:23-06-3.jpg]] [[Презентація уроку: Поворот. Паралельне перенесення|параллельному переносу]], при котором точка А переходит в точку D (рис. 214). При этом переносе точка А смещается по прямой AD, а значит, точка В смещается по параллельной прямой ВС. Прямая АВ переходит в параллельную прямую, а значит, в прямую DC. |
| | + | |
| | + | Следовательно, точка В переходит В точку С. Таким образом, наш параллельный перенос переводит вектор [[Image:23-06-3.jpg]] в вектор [[Image:23-06-5.jpg]], а значит, эти векторы равны. Пусть [[Image:23-06-1.jpg]] — вектор и А — произвольная точка. Тогда от точки А можно отложить один и только один вектор [[Image:23-06-1.jpg]]', равный вектору [[Image:23-06-1.jpg]]. |
| | + | |
| | + | Действительно, существует единственный [[Ілюстрації: Поворот. Паралельне перенесення|параллельный перенос]], при котором начало вектора [[Image:23-06-1.jpg]] переходит в точку А. Вектор, в который переходит при этом вектор [[Image:23-06-1.jpg]], и- есть вектор [[Image:23-06-1.jpg]]'. |
| | + | |
| | + | Для практического откладывания от данной точки (D) вектора, равного данному ([[Image:23-06-3.jpg]]), можно воспользоваться задачей 2. <br> |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Следовательно, точка В переходит В точку С. Таким образом, наш параллельный перенос переводит вектор [[Image:23-06-3.jpg]] в вектор [[Image:23-06-5.jpg]], а значит, эти векторы равны. Пусть [[Image:23-06-1.jpg]] — вектор и А — произвольная точка. Тогда от точки А можно отложить один и только один вектор [[Image:23-06-1.jpg]]', равный вектору [[Image:23-06-1.jpg]].<br>Действительно, существует единственный параллельный перенос, при котором начало вектора [[Image:23-06-1.jpg]] переходит в точку А. Вектор, в который переходит при этом вектор [[Image:23-06-1.jpg]], и- есть вектор [[Image:23-06-1.jpg]]'.<br>Для практического откладывания от данной точки (D) вектора, равного данному ([[Image:23-06-3.jpg]]), можно воспользоваться задачей 2. <br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> | | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> |
| Строка 24: |
Строка 30: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 15:47, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Равенство векторов
Равенство векторов
Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что равные векторы одинаково направлены и равны по абсолютной величине.
Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.
Действительно, пусть  и и 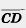 — одинаково направленные векторы, равные по абсолютной величине (рис. 213). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую CD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, т. е. параллельный перенос переводит вектор — одинаково направленные векторы, равные по абсолютной величине (рис. 213). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую CD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, т. е. параллельный перенос переводит вектор 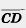 в вектор в вектор  . Значит, векторы . Значит, векторы  и и 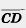 равны, что и требовалось доказать. равны, что и требовалось доказать.
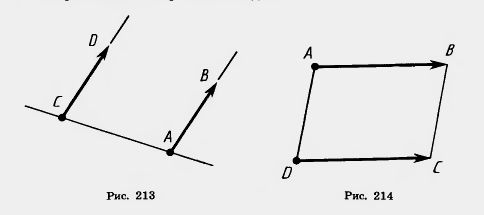
Задача (2). Четырехугольник ABCD — параллелограмм. Докажите равенство векторов  и и 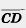 . .
Решение. Подвергнем вектор  параллельному переносу, при котором точка А переходит в точку D (рис. 214). При этом переносе точка А смещается по прямой AD, а значит, точка В смещается по параллельной прямой ВС. Прямая АВ переходит в параллельную прямую, а значит, в прямую DC. параллельному переносу, при котором точка А переходит в точку D (рис. 214). При этом переносе точка А смещается по прямой AD, а значит, точка В смещается по параллельной прямой ВС. Прямая АВ переходит в параллельную прямую, а значит, в прямую DC.
Следовательно, точка В переходит В точку С. Таким образом, наш параллельный перенос переводит вектор  в вектор в вектор 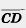 , а значит, эти векторы равны. Пусть , а значит, эти векторы равны. Пусть  — вектор и А — произвольная точка. Тогда от точки А можно отложить один и только один вектор — вектор и А — произвольная точка. Тогда от точки А можно отложить один и только один вектор  ', равный вектору ', равный вектору  . .
Действительно, существует единственный параллельный перенос, при котором начало вектора  переходит в точку А. Вектор, в который переходит при этом вектор переходит в точку А. Вектор, в который переходит при этом вектор  , и- есть вектор , и- есть вектор  '. '.
Для практического откладывания от данной точки (D) вектора, равного данному ( ), можно воспользоваться задачей 2. ), можно воспользоваться задачей 2.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











