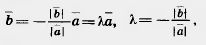|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Разложение вектора по двум неколлинеарным векторам</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Разложение вектора по двум неколлинеарным векторам, вектора, абсолютную величину, прямые</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Разложение вектора по двум неколлинеарным векторам''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Разложение вектора по двум неколлинеарным векторам''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ'''
| + | '''Разложение вектора по двум неколлинеарным векторам''' |
| | | | |
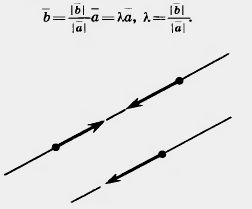
| - | <br>'''''Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых''''' (рис. 223). Коллинеарные векторы либо одинаково направлены, либо противоположно направлены. | + | <br> Два ненулевых [[Презентація уроку: Означення вектора. Модуль і напрям вектора.Рівні вектори|вектора]] называются коллинеарными, если они лежат на одной прямой или на параллельных прямых (рис. 223). Коллинеарные векторы либо одинаково направлены, либо противоположно направлены. |
| | | | |
| - | Пусть [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] — отличные от нуля коллинеарные векторы. Докажем, что существует число [[Image:23-06-43.jpg]] такое, что | + | Пусть [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] — отличные от нуля коллинеарные векторы. Докажем, что существует число [[Image:23-06-43.jpg]] такое, что |
| | | | |
| - | [[Image:23-06-44.jpg]]<br><br>Допустим, векторы [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] одинаково направлены. Векторы | + | [[Image:23-06-44.jpg|Разложение вектора]]<br><br>Допустим, векторы [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] одинаково направлены. Векторы[[Image:23-06-45.jpg|Векторы]]<br><br>одинаково направлены и имеют одну и ту же [[Абсолютная величина и направление вектора|абсолютную величину]] |[[Image:23-06-8.jpg]]|. Значит, они равны: |
| | | | |
| - | [[Image:23-06-45.jpg]]<br><br>одинаково направлены и имеют одну и ту же абсолютную величину |[[Image:23-06-8.jpg]]|. Значит, они равны: | + | [[Image:23-06-46.jpg|240px|Разложение вектора]] |
| | | | |
| - | [[Image:23-06-46.jpg]]
| + | <br> |
| | | | |
| | + | [[Image:23-06-47.jpg|420px|Разложение вектора]]<br> <br>В случае противоположно направленных векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] аналогично заключаем, что |
| | | | |
| | + | [[Image:23-06-48.jpg|240px|Доказательство]] что и требовалось доказать. |
| | | | |
| - | [[Image:23-06-47.jpg]]<br> <br>В случае противоположно направленных векторов [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] аналогично заключаем, что | + | Пусть [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] — отличные от нуля неколлинеарные векторы. Докажем, что любой вектор с можно представить в виде [[Image:23-06-49.jpg|120px|Вектор]] |
| | | | |
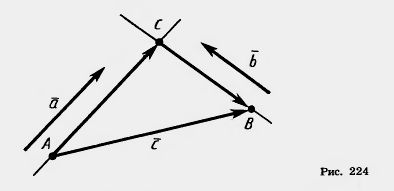
| - | [[Image:23-06-48.jpg]]<br><br>что и требовалось доказать. | + | Пусть А и В — начало и конец вектора [[Image:23-06-23.jpg]] (рис. 224). Проведем через точки А и В [[Параллельные прямые. Полные уроки|прямые]], параллельные векторам [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]]. Они пересекутся в некоторой точке С. Имеем:[[Image:23-06-50.jpg|120px|Решение]] |
| | | | |
| - | Пусть [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] — отличные от нуля неколлинеарные векторы. Докажем, что любой вектор с можно представить в виде
| + | Так как векторы [[Image:23-06-1.jpg]] и [[Image:23-06-17.jpg]] коллинеарны, то [[Image:23-06-51.jpg|Решение]]. Так как векторы [[Image:23-06-52.jpg]] и [[Image:23-06-8.jpg]] коллинеарны, то [[Image:23-06-53.jpg|Решение]]. Таким образом, [[Image:23-06-49.jpg|Решение]] что и требовалось доказать. |
| | | | |
| - | [[Image:23-06-49.jpg]]<br><br>Пусть А и В — начало и конец вектора [[Image:23-06-23.jpg]] (рис. 224). Проведем через точки А и В прямые, параллельные векторам [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]]. Они пересекутся в некоторой точке С. Имеем:
| + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [[Image:23-06-50.jpg]]<br>Так как векторы [[Image:23-06-1.jpg]] и [[Image:23-06-17.jpg]] коллинеарны, то [[Image:23-06-51.jpg]]. Так как векторы [[Image:23-06-52.jpg]] и [[Image:23-06-8.jpg]] коллинеарны, то [[Image:23-06-53.jpg]]. Таким образом,
| |
| | | | |
| - | [[Image:23-06-49.jpg]]
| |
| - |
| |
| - | <br> что и требовалось доказать.<br>
| |
| - |
| |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Школьная библиотека [[Гипермаркет знаний - первый в мире!|онлайн]], учебники и книги по всему предметам, Математика 8 класс [[Математика|скачать]]</sub> | | <sub>Школьная библиотека [[Гипермаркет знаний - первый в мире!|онлайн]], учебники и книги по всему предметам, Математика 8 класс [[Математика|скачать]]</sub> |
| Строка 40: |
Строка 36: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.