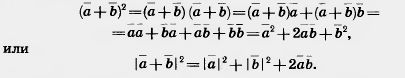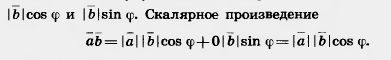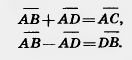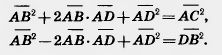|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Скалярное произведение векторов</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Скалярное произведение векторов, число, произведения векторов, векторами, абсолютных величин, параллелограмма</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Скалярное произведение векторов''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Скалярное произведение векторов''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ'''
| + | '''Скалярное произведение векторов''' |
| | | | |
| - | <br>Скалярным произведением векторов [[Image:23-06-1.jpg]](а<sub>1</sub>;а<sub>2</sub>) и [[Image:23-06-8.jpg]] (b<sub>1</sub>;b<sub>2</sub>) называется число a<sub>1</sub>b<sub>1</sub> + a<sub>2</sub>b<sub>2</sub>. | + | <br>Скалярным произведением векторов [[Image:23-06-1.jpg]](а<sub>1</sub>;а<sub>2</sub>) и [[Image:23-06-8.jpg]] (b<sub>1</sub>;b<sub>2</sub>) называется [[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|число]] a<sub>1</sub>b<sub>1</sub> + a<sub>2</sub>b<sub>2</sub>. |
| | | | |
| - | Для скалярного произведения векторов используется такая же запись, как и для произведения чисел. Скалярное произведение [[Image:23-06-1.jpg]]'''.'''[[Image:23-06-1.jpg]] обозначается [[Image:23-06-1.jpg]]<sup>2</sup> и называется скалярным квадратом. Очевидно, [[Image:23-06-1.jpg]]<sup>2</sup>=|[[Image:23-06-1.jpg]]|<sup>2</sup>. | + | Для скалярного произведения векторов используется такая же запись, как и для произведения чисел. Скалярное произведение [[Image:23-06-1.jpg]]'''.'''[[Image:23-06-1.jpg]] обозначается [[Image:23-06-1.jpg]]<sup>2</sup> и называется скалярным квадратом. Очевидно, [[Image:23-06-1.jpg]]<sup>2</sup>=|[[Image:23-06-1.jpg]]|<sup>2</sup>. |
| | | | |
| - | Из определения скалярного произведения векторов следует, что для любых векторов [[Image:23-06-1.jpg]](а<sub>1</sub>;а<sub>2</sub>), [[Image:23-06-8.jpg]](b<sub>1</sub>;b<sub>2</sub>), [[Image:23-06-23.jpg]](c<sub>1</sub>;c<sub>2</sub>) | + | Из определения скалярного [[Презентація уроку: Множення векторів на число|произведения векторов]] следует, что для любых векторов [[Image:23-06-1.jpg]](а<sub>1</sub>;а<sub>2</sub>), [[Image:23-06-8.jpg]](b<sub>1</sub>;b<sub>2</sub>), [[Image:23-06-23.jpg]](c<sub>1</sub>;c<sub>2</sub>) |
| | | | |
| - | <br>([[Image:23-06-1.jpg]]+[[Image:23-06-8.jpg]]) [[Image:23-06-23.jpg]]=[[Image:23-06-1.jpg]][[Image:23-06-23.jpg]] + [[Image:23-06-8.jpg]][[Image:23-06-23.jpg]].
| + | ([[Image:23-06-1.jpg]]+[[Image:23-06-8.jpg]]) [[Image:23-06-23.jpg]]=[[Image:23-06-1.jpg]][[Image:23-06-23.jpg]] + [[Image:23-06-8.jpg]][[Image:23-06-23.jpg]]. |
| | | | |
| - | Действительно, левая часть равенства есть (а<sub>1</sub>;b<sub>1</sub>)c<sub>1 + </sub>(а<sub>2</sub>;b<sub>2</sub>)c<sub>2</sub> , а правая a<sub>1</sub>c<sub>1</sub> + a<sub>2</sub> c<sub>2</sub> + b<sub>1</sub>c<sub>1</sub> + b<sub>2</sub> c<sub>2</sub> . Очевидно, они равны. | + | Действительно, левая часть равенства есть (а<sub>1</sub>;b<sub>1</sub>)c<sub>1 + </sub>(а<sub>2</sub>;b<sub>2</sub>)c<sub>2</sub> , а правая a<sub>1</sub>c<sub>1</sub> + a<sub>2</sub> c<sub>2</sub> + b<sub>1</sub>c<sub>1</sub> + b<sub>2</sub> c<sub>2</sub> . Очевидно, они равны. |
| | | | |
| - | Углом между ненулевыми векторами [[Image:23-06-3.jpg]] и [[Image:23-06-17.jpg]] называется угол ВАС. Углом между любыми двумя ненулевыми векторами [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю. | + | Углом между ненулевыми [[Презентація уроку: Означення вектора. Модуль і напрям вектора.Рівні вектори|векторами]] [[Image:23-06-3.jpg]] и [[Image:23-06-17.jpg]] называется угол ВАС. Углом между любыми двумя ненулевыми векторами [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю. |
| | | | |
| - | Теорема 10.3. '''''Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.''''' | + | '''Теорема 10.3.''' Скалярное произведение векторов равно произведению их [[Абсолютная величина и направление вектора|абсолютных величин]] на косинус угла между ними. |
| | | | |
| - | Доказательство. Пусть [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] — данные векторы и [[Image:23-06-54.jpg]] — угол между ними. Имеем: | + | '''Доказательство.''' Пусть [[Image:23-06-1.jpg]] и [[Image:23-06-8.jpg]] — данные векторы и [[Image:23-06-54.jpg]] — угол между ними. Имеем: |
| | | | |
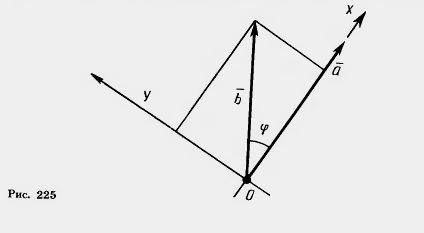
| - | [[Image:23-06-55.jpg]]<br><br>Отсюда видно, что скалярное произведение [[Image:23-06-1.jpg]] [[Image:23-06-8.jpg]] выражается через длины векторов [[Image:23-06-1.jpg]], [[Image:23-06-8.jpg]] и [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]], а поэтому не зависит от выбора системы координат, т. е. скалярное произведение не изменится, если систему координат выбрать спехщальным образом. Возьмем систему координат ху так, как показано на рисунке 225. При таком выборе системы координат координа- | + | [[Image:23-06-55.jpg|420px|Скалярное произведение векторов]]<br><br>Отсюда видно, что скалярное произведение [[Image:23-06-1.jpg]] [[Image:23-06-8.jpg]] выражается через длины векторов [[Image:23-06-1.jpg]], [[Image:23-06-8.jpg]] и [[Image:23-06-1.jpg]] + [[Image:23-06-8.jpg]], а поэтому не зависит от выбора системы координат, т. е. скалярное произведение не изменится, если систему координат выбрать специальным образом. Возьмем систему координат ху так, как показано на рисунке 225. <br> |
| | | | |
| | + | [[Image:23-06-56.jpg|420px|Система координат]]<br> <br>При таком выборе системы координат координатами вектора [[Image:23-06-1.jpg]] будут |[[Image:23-06-1.jpg]]| и О, а координатами вектора [[Image:23-06-8.jpg]] будут |
| | | | |
| | + | [[Image:23-06-57.jpg|420px|Скалярное произведение векторов]]<br>Теорема доказана. |
| | | | |
| - | [[Image:23-06-56.jpg]]<br> <br>тами вектора [[Image:23-06-1.jpg]] будут |[[Image:23-06-1.jpg]]| и О, а координатами вектора [[Image:23-06-8.jpg]] будут
| + | '''Из теоремы 10.3''' следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны. |
| | | | |
| - | [[Image:23-06-57.jpg]] | + | '''Задача (38)'''. Докажите, что сумма квадратов диагоналей [[Паралелограм. Ознаки паралелограма. Властивості паралелограма|параллелограмма]] равна сумме квадратов его сторон. |
| | | | |
| - | <br>Теорема доказана.
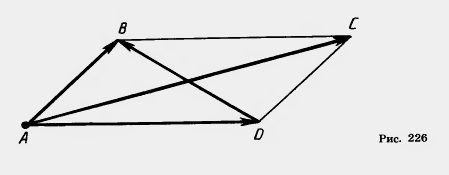
| + | '''Решение'''. Пусть четырехугольник ABCD — параллелограмм (рис. 226). Имеем векторные равенства |
| | | | |
| - | Из теоремы 10.3 следует, что '''''если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.'''''
| + | [[Image:23-06-58.jpg|120px|Решение]]<br><br>Возведем эти равенства в квадрат. Получим: |
| | | | |
| - | Задача (38). Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
| + | [[Image:23-06-59.jpg|240px|Решение]] |
| | | | |
| - | Решение. Пусть четырехугольник ABCD — параллелограмм (рис. 226). Имеем векторные равенства
| + | <br>Сложим эти равенства почленно. Получим: |
| | | | |
| - | [[Image:23-06-58.jpg]]<br><br>Возведем эти равенства в квадрат. Получим: | + | [[Image:23-06-60.jpg|180px|Решение]]<br>Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать. <br> |
| | | | |
| - | [[Image:23-06-59.jpg]] | + | [[Image:23-06-61.jpg|480px|Параллелограм]] |
| | | | |
| - | <br>Сложим эти равенства почленно. Получим:
| |
| | | | |
| - | [[Image:23-06-60.jpg]]
| |
| | | | |
| - | <br>Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать. <br>
| + | ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [[Image:23-06-61.jpg]]
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Планирование математике, материалы по математике 8 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Планирование математике, материалы по математике 8 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| Строка 58: |
Строка 56: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Для скалярного произведения векторов используется такая же запись, как и для произведения чисел. Скалярное произведение  .
. обозначается
обозначается  2 и называется скалярным квадратом. Очевидно,
2 и называется скалярным квадратом. Очевидно,  2=|
2=| |2.
|2.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.