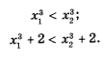|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Свойства функций<metakeywords>Свойства функций</metakeywords>''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Свойства функций<metakeywords>Свойства функций, графика функции, неравенство, функция, числовых неравенств, числовой прямой, графику, множество, отрезка, параллельная, парабола, координат, луче</metakeywords>''' |
| | | | |
| | <br> | | <br> |
| | | | |
| - | '''СВОЙСТВА ФУНКЦИЙ'''<br>В 7-м и 8-м классах вы изучали некоторые свойства функций. Сейчас мы их соберем вместе, в один параграф, напомним их суть и геометрический смысл и договоримся о том, в каком порядке будем перечислять эти свойства при чтении графика функции. Обратите внимание: во всех определениях фигурирует числовое множество X, являющееся частью области определения функции: X с D(f). На практике чаще всего встречаются случаи, когда X — числовой промежуток (отрезок, интервал, луч и т.д.).<br>'''Определение 1.''' Функцию у = f(х) называют возрастающей на множестве X с D(f), если для любых двух точек х<sub>1</sub> и х<sub>2</sub> множества X, таких, что х<sub>1</sub> < х<sub>2</sub>, выполняется неравенство f(х<sub>1</sub> < f(х<sub>2</sub>).<br>'''Определение 2.''' Функцию у = f(х) называют убывающей на множестве X с D(f), если для любых монотонность двух точек х<sub>1</sub> и х<sub>2</sub> множества X, таких, что х<sub>1</sub> < х<sub>2</sub>, функции выполняется неравенство f(x<sub>1</sub>) > f(x<sub>2</sub>).<br>На практике удобнее пользоваться следующими формулировками: функция возрастает, если большему значению аргумента соответствует большее значение функции; функция убывает, если большему значению аргумента соответствует меньшее значение функции.<br>В 7-м и 8-м классах мы использовали следующее геометрическое истолкование понятий возрастания или убывания функции: двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в горку (рис. 55); двигаясь по графику убывающей функции слева направо, как бы спускаемся с горки (рис. 56).<br>Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.<br>Отметим еще одно обстоятельство: если функция возрастает (или убывает) в своей естественной области определения, то обычно говорят, что функция возрастающая (или убывающая) — без указания числового множества X. | + | '''Свойства функций'''<br> |
| | | | |
| - | [[Image:Al101.jpg]]<br><br>'''Пример 1.''' Исследовать на монотонность функцию:<br>'''а) ''' у = х<sup>3</sup> + 2; б) у = 5 - 2х.<br>'''Решение: а)''' Возьмем произвольные значения аргумента х<sub>1</sub> и х<sub>2</sub> и пусть х<sub>1</sub><х<sub>2</sub>. Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь: | + | <br>В 7-м и 8-м классах вы изучали некоторые свойства функций. Сейчас мы их соберем вместе, в один параграф, напомним их суть и геометрический смысл и договоримся о том, в каком порядке будем перечислять эти свойства при чтении [[Линейная функция и ее график|графика функции]]. Обратите внимание: во всех определениях фигурирует числовое множество X, являющееся частью области определения функции: X с D(f). На практике чаще всего встречаются случаи, когда X — числовой промежуток (отрезок, интервал, луч и т.д.).<br> |
| | | | |
| - | [[Image:Al102.jpg]]<br>Последнее неравенство означает, что f(х<sub>1</sub>) < f(х<sub>2</sub>). Итак, из х<sub>1</sub> < х<sub>2</sub> следует f{х<sub>1</sub>) < f(х<sub>2</sub>), а это означает, что заданная функция возрастает (на всей числовой прямой).<br>'''б) ''' Если х<sub>1</sub> < х<sub>2</sub>, то -2х<sub>1</sub> > -2х<sub>2</sub>; далее имеем 5 - 2.x<sub>1</sub> > 5 - 2х<sub>2</sub>, т.е. f(х<sub>1</sub>) > f(х<sub>2</sub>).<br>Итак, из х<sub>1</sub> < х<sub>2</sub> следует f(х<sub>1</sub>) > f(х<sub>2</sub>), а это означает, что заданная функция убывает (на всей числовой прямой). <br>'''Определение 3.''' Функцию у — f(х) называют ограниченной снизу на множестве X с D (f), если все значения функции на множестве X больше некоторого числа (иными словами, если существует число m такое, что для любого значения х є X выполняется неравенство f(х) >m).
| + | '''Определение 1.''' <br> |
| | | | |
| - | '''Определение 4.''' Функцию у = f(х) называют ограниченной сверху на множестве X с D (f), если все значения функции меньше некоторого числа (иными словами, если существует число М такое, что для любого значения х є X выполняется неравенство f(х) < М).<br>Если множество X не указано, то подразумевается, что речь идет об ограниченности функции снизу или сверху во всей области определения.<br>Если функция ограничена и снизу, и сверху, то ее называют ограниченной.<br>Ограниченность функции легко прочитывается по ее графику: если функция ограничена снизу, то ее график целиком расположен выше некоторой горизонтальной прямой у = т (рис. 57); если функция ограничена сверху, то ее график целиком расположен ниже некоторой горизонтальной прямой у = М (рис. 58).
| + | Функцию у = f(х) называют возрастающей на множестве X с D(f), если для любых двух точек х<sub>1</sub> и х<sub>2</sub> множества X, таких, что х<sub>1</sub> < х<sub>2</sub>, выполняется [[Числові нерівності. Основні властивості чйслових нерівностей. Почленне додавання і множення нерівностей. Презентація уроку|неравенство]] f(х<sub>1</sub> < f(х<sub>2</sub>).<br> |
| | | | |
| - | [[Image:Al103.jpg]]<br>'''Пример 2.''' Исследовать на ограниченность функцию [[Image:Al104.jpg]]<br>'''Решение.'''С одной стороны, вполне очевидно неравенство [[Image:Al105.jpg]] (по определению квадратного корня [[Image:Al106.jpg]] Это означает, что функция ограничена снизу. С другой стороны, имеем [[Image:Al107.jpg]] а потому [[Image:Al108.jpg]]<br>Это означает, что функция ограничена сверху. А теперь посмотрите на график заданной функции (рис. 52 из предыдущего параграфа). Ограниченность функции и сверху, и снизу прочитывается по графику достаточно легко. <br>'''Определение 5.''' Число m называют наименьшим значением функции у = f(х) на множестве X С D(f), если:<br>'''1)''' в Х существует такая точка х<sub>0</sub>, что f(х<sub>0</sub>) = m;<br>'''2) ''' для всех x из X выполняется неравенство m>f(х<sub>0</sub>).<br>'''Определение 6.''' Число М называют наибольшим значением функции у = f(x) на множестве X С D(f), если:<br>'''1)''' в Х существует такая точка х<sub>0</sub>, что f(x<sub>0</sub>) = М;<br>'''2)''' для всех x из X выполняется неравенство [[Image:Al109.jpg]]<br>Наименьшее значение функции мы обозначали и в 7-м, и в 8-м классах символом у , а наибольшее — символом у. Если множество X не указано, то подразумевается, что речь идет об отыскании наименьшего или наибольшего значения функции во всей области определения.<br>Достаточно очевидны следующие полезные утверждения:<br>'''1)''' Если у функции существует Y, то она ограничена снизу.<br>'''2)''' Если у функции существует Y, то она ограничена сверху.<br>'''3)''' Если функция не ограничена снизу, то Y не существует.<br>'''4) ''' Если функция не ограничена сверху, то Y не существует.<br>'''Пример 3.''' Найти наименьшее и наибольшее значения функции [[Image:Al1010.jpg]]<br>'''Решение.''' Достаточно очевидно, особенно если прибегнуть к помощи графика функции (рис. 52), что [[Image:Al1011.jpg]] = 0 (этого значения функция достигает в точках х = -3 и х = 3), а [[Image:Al1011.jpg]] = 3 (этого значения функция достигает в точке х = 0.<br>В 7-м и 8-м классах мы упоминали еще два свойства функций. Первое назвали свойством выпуклости функции. Считается, что функция выпукла вниз на промежутке X, если, соединив любые две точки ее графика (с абсциссами из X) отрезком прямой, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 59). непрерывность Функция выпукла вверх на промежутке X, если, функции соединив любые две точки ее графика (с абсциссами из X) отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка (рис. 60).
| + | '''Определение 2.''' <br> |
| | | | |
| - | [[Image:Al1012.jpg]]<br>Второе свойство — непрерывность функции на промежутке X — означает, что график функции на промежутке X — сплошной, т.е. не имеет проколов и скачков.<br>'''Замечание.''' На самом деле в математике все обстоит, как говорится, «с точностью до наоборот»: график функции изображается в виде сплошной линии (без проколов и скачков) только тогда, когда доказана непрерывность функции. Но формальное определение непрерывности функции, достаточно сложное и тонкое, нам пока не по силам. То же самое можно сказать и о выпуклости функции. Обсуждая указанные два свойства функций, будем по-прежнему опираться на наглядно-интуитивные представления.<br>А теперь проведем смотр наших знаний. Вспомнив о тех функциях, которые мы с вами изучали в 7-м и 8-м классах, уточним, как выглядят их графики, и перечислим свойства функции, придерживаясь определенного порядка, например такого: область определения; монотонность; ограниченность; [[Image:Al1011.jpg]] , [[Image:Al1011.jpg]]; непрерывность; область значений; выпуклость.<br>Впоследствии появятся новые свойства функций, соответственно будет меняться и перечень свойств.<br>'''1. Постоянная функция у = С'''<br>График функции у = С изображен на рис. 61 — прямая, параллельная оси х. Это настолько неинтересная функция, что нет смысла перечислять ее свойства.
| + | Функцию у = f(х) называют убывающей на множестве X с D(f), если для любых монотонность двух точек х<sub>1</sub> и х<sub>2</sub> множества X, таких, что х<sub>1</sub> < х<sub>2</sub>, функции выполняется неравенство f(x<sub>1</sub>) > f(x<sub>2</sub>).<br> |
| | | | |
| - | [[Image:Al1013.jpg]]<br>Графиком функции у = кх + m является прямая (рис. 62, 63).
| + | На практике удобнее пользоваться следующими формулировками: функция возрастает, если большему значению аргумента соответствует большее значение функции; функция убывает, если большему значению аргумента соответствует меньшее значение функции.<br> |
| | | | |
| - | [[Image:Al1014.jpg]]обратите внимание<br>Свойства функции у = кх + m:<br>'''1)''' [[Image:Al1015.jpg]]<br>'''2)''' возрастает, если к > 0 (рис. 62), убывает, если к < 0 (рис. 63);<br>'''3) ''' не ограничена ни снизу, ни сверху;<br>'''4)''' нет ни наибольшего, ни наименьшего значений;<br>'''5)''' функция непрерывна;<br>'''6)''' [[Image:Al1016.jpg]]<br>'''7)''' о выпуклости говорить не имеет смысла.<br>[[Image:Al1017.jpg]]<br>Графиком функции у = кх<sup>2</sup> является парабола с вершиной в начале координат и с ветвями, направленными вверх, если к > О (рис. 64), и вниз, если к < 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.
| + | В 7-м и 8-м классах мы использовали следующее геометрическое истолкование понятий возрастания или убывания функции: двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в горку (рис. 55); двигаясь по графику убывающей функции слева направо, как бы спускаемся с горки (рис. 56).<br>Обычно термины «возрастающая функция», «убывающая [[Основные понятия|функция]]» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.<br> |
| | | | |
| - | [[Image:Al1018.jpg]]<br> <br>Свойства функции у - кх<sup>2</sup>:<br>'''Для случая к> 0''' (рис. 64):<br>'''1)''' D(f) = (-оо,+оо);<br>'''2)''' убывает на луче (-оо, 0], возрастает на луче [0, +оо);<br>'''3)''' ограничена снизу, не ограничена сверху;<br>'''4) ''' [[Image:Al1011.jpg]] = [[Image:Al1011.jpg]] не существует;<br>'''5)''' непрерывна;<br>'''6) '''Е(f) = [0,+оо);<br>'''7) ''' выпукла вниз.<br>Обратите внимание: на промежутке (-оо, 0] функция убывает, а на промежутке [0, +оо) функция возрастает. Эти промежутки называют промежутками монотонности функции у = кх<sup>2</sup>. Понятие промежутка монотонности будем использовать и для других функций.<br>'''Для случая к < 0''' (рис. 65):<br>'''1) ''' D(f) = (-оо,+00);<br>'''2)''' возрастает на луче (-оо, 0], убывает на луче [0, +оо);<br>'''3)''' не ограничена снизу, ограничена сверху;<br>'''4)''' [[Image:Al1011.jpg]] не существует, [[Image:Al1011.jpg]] = 0;<br>'''5)''' непрерывна;<br>'''6)''' Е(f) > = (-оо, 0];<br>'''7) ''' выпукла вверх.<br>График функции у = f(х) строится по точкам; чем больше точек вида (х; f(х)) мы возьмем, тем более точное представление о графике получим. Если этих точек взять достаточно много, то и представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает нам, что график надо изобразить в виде сплошной линии (в данном случае в виде параболы). А уж затем, читая график, мы делаем выводы о непрерывности функции, о ее выпуклости вниз или вверх, об области значений функции. Вы должны понимать, что из перечисленных семи свойств «законными» являются лишь свойства 1), 2), 3), 4) — «законными» в том смысле, что мы в состоянии обосновать их, ссылаясь на точные определения. Об остальных свойствах у нас имеются только наглядно-интуитивные представления. Кстати, в этом нет ничего плохого. Из истории развития математики известно, что человечество часто и долго пользовалось различными свойствами тех или иных объектов, не зная точных определений. Потом, когда такие определения удавалось сформулировать, все становилось на свои места. <br>[[Image:Al1019.jpg]]<br>Графиком функции является гипербола, оси координат служат асимптотами гиперболы (рис. 66, 67).<br>
| + | Отметим еще одно обстоятельство: если функция возрастает (или убывает) в своей естественной области определения, то обычно говорят, что функция возрастающая (или убывающая) — без указания числового множества X. |
| | | | |
| - | [[Image:Al1020.jpg]]<br><br>'''1)''' D(f) = (-00,0)1U (0,+оо);<br>'''2) ''' если к > 0, то функция убывает на открытом луче (-оо, 0) и на открытом луче (0, +оо) (рис. 66); если к < 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);<br>'''3)''' не ограничена ни снизу, ни сверху;<br>'''4)''' нет ни наименьшего, ни наибольшего значений;<br>'''5)''' функция непрерывна на открытом луче (-оо, 0) и на открытом луче (0, +оо);<br>'''6) '''Е(f) = (-оо,0) U (0,+оо);<br>'''7)''' если к > 0, то функция выпукла вверх при х < 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х > 0, т.е. на открытом луче (0, +оо) (рис. 66). Если к < 0, то функция выпукла вверх при х > О и выпукла вниз при х < О (рис. 67).<br>'''5. Функция''' [[Image:Al1021.jpg]]<br>Графиком функции является ветвь параболы (рис. 68). Свойства функции [[Image:Al1021.jpg]] :<br>'''1)''' D(f) = [0, +оо);<br>'''2) ''' возрастает;<br>'''3) ''' ограничена снизу, не ограничена сверху;<br>'''4)''' [[Image:Al1011.jpg]] = [[Image:Al1011.jpg]] не существует;<br>'''5)''' непрерывна;<br>'''6)''' Е(f) = [0,+оо);<br>'''7)''' выпукла вверх.<br>'''6. Функция у = | х |'''<br>Графиком функции является объединение двух лучей: [[Image:Al1022.jpg]]<br>Свойства функции у= | х |:<br>'''1) ''' D(f) = (-оо,+оо);<br>'''2) ''' убывает на луче (-оо, 0], возрастает на луче [0, +оо);<br>'''3) ''' ограничена снизу, не ограничена сверху;<br>'''4) ''' [[Image:Al1011.jpg]] =[[Image:Al1011.jpg]] не существует;<br>'''5)''' непрерывна;<br>'''6)''' Е(f) = [0,+оо);<br>'''7)''' функцию можно считать выпуклой вниз.<br>'''7. Функция у = ах<sup>2</sup> + Ьх + с'''<br>Графиком функции является парабола с вершиной в точке [[Image:Al1023.jpg]]<br>и с ветвями, направленными вверх, если а > 0 (рис. 70), и вниз,<br>если а < 0 (рис. 71). Прямая [[Image:Al1024.jpg]] является осью параболы.<br>[[Image:Al1025.jpg]] | + | [[Image:Al101.jpg|480px|График функции]]<br><br>'''Пример 1.''' <br> |
| | + | |
| | + | Исследовать на монотонность функцию:<br> |
| | + | |
| | + | '''а) ''' у = х<sup>3</sup> + 2; б) у = 5 - 2х.<br> |
| | + | |
| | + | '''Решение: '''<br> |
| | + | |
| | + | а) Возьмем произвольные значения аргумента х<sub>1</sub> и х<sub>2</sub> и пусть х<sub>1</sub><х<sub>2</sub>. Тогда, по свойствам [[Завдання до уроку: Числові нерівності. Основні властивості чйслових нерівностей. Почленне додавання і множення нерівностей.|числовых неравенств]] (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь: |
| | + | |
| | + | [[Image:Al102.jpg|120px|Неравенства]]<br>Последнее неравенство означает, что f(х<sub>1</sub>) < f(х<sub>2</sub>). Итак, из х<sub>1</sub> < х<sub>2</sub> следует f{х<sub>1</sub>) < f(х<sub>2</sub>), а это означает, что заданная функция возрастает (на всей числовой прямой).<br> |
| | + | |
| | + | б) Если х<sub>1</sub> < х<sub>2</sub>, то -2х<sub>1</sub> > -2х<sub>2</sub>; далее имеем 5 - 2.x<sub>1</sub> > 5 - 2х<sub>2</sub>, т.е. f(х<sub>1</sub>) > f(х<sub>2</sub>).<br> |
| | + | |
| | + | Итак, из х<sub>1</sub> < х<sub>2</sub> следует f(х<sub>1</sub>) > f(х<sub>2</sub>), а это означает, что заданная функция убывает (на всей [[Числові проміжки. Об'еднання та переріз числових проміжків|числовой прямой]]). <br> |
| | + | |
| | + | <br>'''Определение 3.''' <br> |
| | + | |
| | + | Функцию у — f(х) называют ограниченной снизу на множестве X с D (f), если все значения функции на множестве X больше некоторого числа (иными словами, если существует число m такое, что для любого значения х є X выполняется неравенство f(х) >m). |
| | + | |
| | + | '''Определение 4.''' <br> |
| | + | |
| | + | Функцию у = f(х) называют ограниченной сверху на множестве X с D (f), если все значения функции меньше некоторого числа (иными словами, если существует число М такое, что для любого значения х є X выполняется неравенство f(х) < М).<br> |
| | + | |
| | + | Если множество X не указано, то подразумевается, что речь идет об ограниченности функции снизу или сверху во всей области определения.<br> |
| | + | |
| | + | Если функция ограничена и снизу, и сверху, то ее называют ограниченной.<br> |
| | + | |
| | + | Ограниченность функции легко прочитывается по ее [[Приклади графіків залежностей між величинами|графику]]: если функция ограничена снизу, то ее график целиком расположен выше некоторой горизонтальной прямой у = т (рис. 57); если функция ограничена сверху, то ее график целиком расположен ниже некоторой горизонтальной прямой у = М (рис. 58). |
| | + | |
| | + | [[Image:Al103.jpg|480px|График функции]]<br>'''Пример 2.''' Исследовать на ограниченность функцию [[Image:Al104.jpg|80px|Функция]]<br>'''Решение.'''С одной стороны, вполне очевидно неравенство [[Image:Al105.jpg|80px|Неравенство]] (по определению квадратного корня [[Image:Al106.jpg|Неравенство]] Это означает, что функция ограничена снизу. С другой стороны, имеем [[Image:Al107.jpg|80px|Неравенство]] а потому [[Image:Al108.jpg|80px|Неравенство]]<br>Это означает, что функция ограничена сверху. А теперь посмотрите на график заданной функции (рис. 52 из предыдущего параграфа). Ограниченность функции и сверху, и снизу прочитывается по графику достаточно легко. <br> |
| | + | |
| | + | <br>'''Определение 5.''' <br> |
| | + | |
| | + | Число m называют наименьшим значением функции у = f(х) на множестве X С D(f), если: |
| | + | |
| | + | 1) в Х существует такая точка х<sub>0</sub>, что f(х<sub>0</sub>) = m; |
| | + | |
| | + | 2) для всех x из X выполняется неравенство m>f(х<sub>0</sub>).<br> |
| | + | |
| | + | '''Определение 6.''' <br> |
| | + | |
| | + | Число М называют наибольшим значением функции у = f(x) на множестве X С D(f), если:<br>1) в Х существует такая точка х<sub>0</sub>, что f(x<sub>0</sub>) = М;<br>2) для всех x из X выполняется неравенство [[Image:Al109.jpg|80px|Неравенство]]<br>Наименьшее значение функции мы обозначали и в 7-м, и в 8-м классах символом у, а наибольшее — символом у. |
| | + | |
| | + | Если [[Множество действительных чисел|множество]] X не указано, то подразумевается, что речь идет об отыскании наименьшего или наибольшего значения функции во всей области определения.<br> |
| | + | |
| | + | Достаточно очевидны следующие полезные утверждения:<br> |
| | + | |
| | + | 1) Если у функции существует Y, то она ограничена снизу.<br>2) Если у функции существует Y, то она ограничена сверху.<br>3) Если функция не ограничена снизу, то Y не существует.<br>4) Если функция не ограничена сверху, то Y не существует.<br> |
| | + | |
| | + | <br>'''Пример 3.''' <br> |
| | + | |
| | + | Найти наименьшее и наибольшее значения функции [[Image:Al1010.jpg|120px|Функция]]<br>'''Решение.'''<br> |
| | + | |
| | + | Достаточно очевидно, особенно если прибегнуть к помощи графика функции (рис. 52), что [[Image:Al1011.jpg]] = 0 (этого значения функция достигает в точках х = -3 и х = 3), а [[Image:Al1011.jpg]] = 3 (этого значения функция достигает в точке х = 0.<br>В 7-м и 8-м классах мы упоминали еще два свойства функций. Первое назвали свойством выпуклости функции. Считается, что функция выпукла вниз на промежутке X, если, соединив любые две точки ее графика (с абсциссами из X) отрезком прямой, мы обнаружим, что соответствующая часть графика лежит ниже проведенного [[Фішки для допитливих до уроку «Вимірювання і побудова відрізків»|отрезка]] (рис. 59). непрерывность Функция выпукла вверх на промежутке X, если, функции соединив любые две точки ее графика (с абсциссами из X) отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка (рис. 60). |
| | + | |
| | + | [[Image:Al1012.jpg|480px|График функции]]<br>Второе свойство — непрерывность функции на промежутке X — означает, что график функции на промежутке X — сплошной, т.е. не имеет проколов и скачков.<br> |
| | + | |
| | + | <br>'''Замечание.''' <br> |
| | + | |
| | + | На самом деле в математике все обстоит, как говорится, «с точностью до наоборот»: график функции изображается в виде сплошной линии (без проколов и скачков) только тогда, когда доказана непрерывность функции. Но формальное определение непрерывности функции, достаточно сложное и тонкое, нам пока не по силам. То же самое можно сказать и о выпуклости функции. Обсуждая указанные два свойства функций, будем по-прежнему опираться на наглядно-интуитивные представления.<br> |
| | + | |
| | + | А теперь проведем смотр наших знаний. Вспомнив о тех функциях, которые мы с вами изучали в 7-м и 8-м классах, уточним, как выглядят их графики, и перечислим свойства функции, придерживаясь определенного порядка, например такого: область определения; монотонность; ограниченность; [[Image:Al1011.jpg]] , [[Image:Al1011.jpg]]; непрерывность; область значений; выпуклость.<br> |
| | + | |
| | + | Впоследствии появятся новые свойства функций, соответственно будет меняться и перечень свойств.<br> |
| | + | |
| | + | <br>'''1. Постоянная функция у = С'''<br> |
| | + | |
| | + | График функции у = С изображен на рис. 61 — прямая, [[Признак параллельности прямых. Полные уроки|параллельная]] оси х. Это настолько неинтересная функция, что нет смысла перечислять ее свойства. |
| | + | |
| | + | [[Image:Al1013.jpg|240px|График функции]]<br> |
| | + | |
| | + | <br>Графиком функции у = кх + m является прямая (рис. 62, 63). |
| | + | |
| | + | [[Image:Al1014.jpg|480px|График функции]]<br> |
| | + | |
| | + | <br>Свойства функции у = кх + m:<br> |
| | + | |
| | + | 1) [[Image:Al1015.jpg|120px|Свойства функции]]<br>2) возрастает, если к > 0 (рис. 62), убывает, если к < 0 (рис. 63);<br>3) не ограничена ни снизу, ни сверху;<br>4) нет ни наибольшего, ни наименьшего значений;<br>5) функция непрерывна;<br>6) [[Image:Al1016.jpg|120px|Свойства функции]]<br>7) о выпуклости говорить не имеет смысла.<br> |
| | + | |
| | + | <br>[[Image:Al1017.jpg]]<br>Графиком функции у = кх<sup>2</sup> является [[Основные результаты-6|парабола]] с вершиной в начале координат и с ветвями, направленными вверх, если к > О (рис. 64), и вниз, если к < 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы. |
| | + | |
| | + | [[Image:Al1018.jpg|480px|График функции]]<br> <br>Свойства функции у - кх<sup>2</sup>:<br> |
| | + | |
| | + | Для случая к> 0 (рис. 64):<br> |
| | + | |
| | + | 1) D(f) = (-оо,+оо);<br>2) убывает на луче (-оо, 0], возрастает на луче [0, +оо);<br>3) ограничена снизу, не ограничена сверху;<br>4) [[Image:Al1011.jpg]] = [[Image:Al1011.jpg]] не существует;<br>5) непрерывна;<br>6) Е(f) = [0,+оо);<br>7) выпукла вниз.<br> |
| | + | |
| | + | <br>'''Обратите внимание:''' на промежутке (-оо, 0] функция убывает, а на промежутке [0, +оо) функция возрастает. Эти промежутки называют промежутками монотонности функции у = кх<sup>2</sup>. Понятие промежутка монотонности будем использовать и для других функций.<br> |
| | + | |
| | + | Для случая к < 0 (рис. 65):<br>1) D(f) = (-оо,+00);<br>2) возрастает на луче (-оо, 0], убывает на луче [0, +оо);<br>3) не ограничена снизу, ограничена сверху;<br>4) [[Image:Al1011.jpg]] не существует, [[Image:Al1011.jpg]] = 0;<br>5) непрерывна;<br>6) Е(f) > = (-оо, 0];<br>7) выпукла вверх.<br> |
| | + | |
| | + | <br>График функции у = f(х) строится по точкам; чем больше точек вида (х; f(х)) мы возьмем, тем более точное представление о графике получим. Если этих точек взять достаточно много, то и представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает нам, что график надо изобразить в виде сплошной линии (в данном случае в виде параболы). А уж затем, читая график, мы делаем выводы о непрерывности функции, о ее выпуклости вниз или вверх, об области значений функции. Вы должны понимать, что из перечисленных семи свойств «законными» являются лишь свойства 1), 2), 3), 4) — «законными» в том смысле, что мы в состоянии обосновать их, ссылаясь на точные определения. Об остальных свойствах у нас имеются только наглядно-интуитивные представления. Кстати, в этом нет ничего плохого. Из истории развития математики известно, что человечество часто и долго пользовалось различными свойствами тех или иных объектов, не зная точных определений. Потом, когда такие определения удавалось сформулировать, все становилось на свои места. <br>[[Image:Al1019.jpg]]<br>Графиком функции является гипербола, оси [[Шкалы и координаты|координат]] служат асимптотами гиперболы (рис. 66, 67).<br> |
| | + | |
| | + | [[Image:Al1020.jpg|480px|График функции]]<br><br>1) D(f) = (-00,0)1U (0,+оо);<br>2) если к > 0, то функция убывает на открытом луче (-оо, 0) и на открытом луче (0, +оо) (рис. 66); если к < 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);<br>3) не ограничена ни снизу, ни сверху;<br>4) нет ни наименьшего, ни наибольшего значений;<br>5) функция непрерывна на открытом [[Плоскость. Прямая. Луч|луче]] (-оо, 0) и на открытом луче (0, +оо);<br>6) Е(f) = (-оо,0) U (0,+оо);<br>7) если к > 0, то функция выпукла вверх при х < 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х > 0, т.е. на открытом луче (0, +оо) (рис. 66). Если к < 0, то функция выпукла вверх при х > О и выпукла вниз при х < О (рис. 67).<br>'''5. Функция''' [[Image:Al1021.jpg]]<br>Графиком функции является ветвь параболы (рис. 68). Свойства функции [[Image:Al1021.jpg]] :<br>1) D(f) = [0, +оо);<br>2) возрастает;<br>3) ограничена снизу, не ограничена сверху;<br>4) [[Image:Al1011.jpg]] = [[Image:Al1011.jpg]] не существует;<br>5) непрерывна;<br>6) Е(f) = [0,+оо);<br>7) выпукла вверх.<br> |
| | + | |
| | + | <br>'''6. Функция у = | х |'''<br> |
| | + | |
| | + | Графиком функции является объединение двух лучей: <br> |
| | + | |
| | + | [[Image:Al1022.jpg|480px|График функции]]<br>Свойства функции у= | х |: |
| | + | |
| | + | 1) D(f) = (-оо,+оо);<br>2) убывает на луче (-оо, 0], возрастает на луче [0, +оо);<br>3) ограничена снизу, не ограничена сверху;<br>4) [[Image:Al1011.jpg]] =[[Image:Al1011.jpg]] не существует;<br>5) непрерывна;<br>6) Е(f) = [0,+оо);<br>7) функцию можно считать выпуклой вниз. |
| | + | |
| | + | <br>'''7. Функция у = ах<sup>2</sup> + Ьх + с'''<br>Графиком функции является парабола с вершиной в точке [[Image:Al1023.jpg|320px|Функция]]<br>и с ветвями, направленными вверх, если а > 0 (рис. 70), и вниз,<br>если а < 0 (рис. 71). Прямая [[Image:Al1024.jpg|Прямая ]] является осью параболы. |
| | + | |
| | + | <br>[[Image:Al1025.jpg|480px|График функции]] |
| | | | |
| | Смотр наших знаний о функциях можно считать законченным. Разумеется, приведенным перечнем в реальной жизни не обойтись. Некоторые новые функции и их свойства встретятся нам уже в этой главе. <br> <br> | | Смотр наших знаний о функциях можно считать законченным. Разумеется, приведенным перечнем в реальной жизни не обойтись. Некоторые новые функции и их свойства встретятся нам уже в этой главе. <br> <br> |
| | | | |
| - | А.Г. Мордкович Алгебра 9 класс | + | ''А.Г. Мордкович [http://xvatit.com/vuzi/ Алгебра] 9 класс'' |
| | | | |
| | <br> | | <br> |
| Строка 32: |
Строка 138: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 08:42, 10 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Свойства функций
Свойства функций
В 7-м и 8-м классах вы изучали некоторые свойства функций. Сейчас мы их соберем вместе, в один параграф, напомним их суть и геометрический смысл и договоримся о том, в каком порядке будем перечислять эти свойства при чтении графика функции. Обратите внимание: во всех определениях фигурирует числовое множество X, являющееся частью области определения функции: X с D(f). На практике чаще всего встречаются случаи, когда X — числовой промежуток (отрезок, интервал, луч и т.д.).
Определение 1.
Функцию у = f(х) называют возрастающей на множестве X с D(f), если для любых двух точек х1 и х2 множества X, таких, что х1 < х2, выполняется неравенство f(х1 < f(х2).
Определение 2.
Функцию у = f(х) называют убывающей на множестве X с D(f), если для любых монотонность двух точек х1 и х2 множества X, таких, что х1 < х2, функции выполняется неравенство f(x1) > f(x2).
На практике удобнее пользоваться следующими формулировками: функция возрастает, если большему значению аргумента соответствует большее значение функции; функция убывает, если большему значению аргумента соответствует меньшее значение функции.
В 7-м и 8-м классах мы использовали следующее геометрическое истолкование понятий возрастания или убывания функции: двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в горку (рис. 55); двигаясь по графику убывающей функции слева направо, как бы спускаемся с горки (рис. 56).
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
Отметим еще одно обстоятельство: если функция возрастает (или убывает) в своей естественной области определения, то обычно говорят, что функция возрастающая (или убывающая) — без указания числового множества X.
Пример 1.
Исследовать на монотонность функцию:
а) у = х3 + 2; б) у = 5 - 2х.
Решение:
а) Возьмем произвольные значения аргумента х1 и х2 и пусть х1<х2. Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:
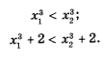
Последнее неравенство означает, что f(х1) < f(х2). Итак, из х1 < х2 следует f{х1) < f(х2), а это означает, что заданная функция возрастает (на всей числовой прямой).
б) Если х1 < х2, то -2х1 > -2х2; далее имеем 5 - 2.x1 > 5 - 2х2, т.е. f(х1) > f(х2).
Итак, из х1 < х2 следует f(х1) > f(х2), а это означает, что заданная функция убывает (на всей числовой прямой).
Определение 3.
Функцию у — f(х) называют ограниченной снизу на множестве X с D (f), если все значения функции на множестве X больше некоторого числа (иными словами, если существует число m такое, что для любого значения х є X выполняется неравенство f(х) >m).
Определение 4.
Функцию у = f(х) называют ограниченной сверху на множестве X с D (f), если все значения функции меньше некоторого числа (иными словами, если существует число М такое, что для любого значения х є X выполняется неравенство f(х) < М).
Если множество X не указано, то подразумевается, что речь идет об ограниченности функции снизу или сверху во всей области определения.
Если функция ограничена и снизу, и сверху, то ее называют ограниченной.
Ограниченность функции легко прочитывается по ее графику: если функция ограничена снизу, то ее график целиком расположен выше некоторой горизонтальной прямой у = т (рис. 57); если функция ограничена сверху, то ее график целиком расположен ниже некоторой горизонтальной прямой у = М (рис. 58).
Пример 2. Исследовать на ограниченность функцию 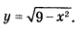
Решение.С одной стороны, вполне очевидно неравенство 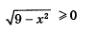 (по определению квадратного корня (по определению квадратного корня 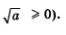 Это означает, что функция ограничена снизу. С другой стороны, имеем Это означает, что функция ограничена снизу. С другой стороны, имеем 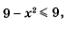 а потому а потому 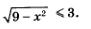
Это означает, что функция ограничена сверху. А теперь посмотрите на график заданной функции (рис. 52 из предыдущего параграфа). Ограниченность функции и сверху, и снизу прочитывается по графику достаточно легко.
Определение 5.
Число m называют наименьшим значением функции у = f(х) на множестве X С D(f), если:
1) в Х существует такая точка х0, что f(х0) = m;
2) для всех x из X выполняется неравенство m>f(х0).
Определение 6.
Число М называют наибольшим значением функции у = f(x) на множестве X С D(f), если:
1) в Х существует такая точка х0, что f(x0) = М;
2) для всех x из X выполняется неравенство 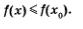
Наименьшее значение функции мы обозначали и в 7-м, и в 8-м классах символом у, а наибольшее — символом у.
Если множество X не указано, то подразумевается, что речь идет об отыскании наименьшего или наибольшего значения функции во всей области определения.
Достаточно очевидны следующие полезные утверждения:
1) Если у функции существует Y, то она ограничена снизу.
2) Если у функции существует Y, то она ограничена сверху.
3) Если функция не ограничена снизу, то Y не существует.
4) Если функция не ограничена сверху, то Y не существует.
Пример 3.
Найти наименьшее и наибольшее значения функции 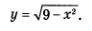
Решение.
Достаточно очевидно, особенно если прибегнуть к помощи графика функции (рис. 52), что 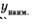 = 0 (этого значения функция достигает в точках х = -3 и х = 3), а = 0 (этого значения функция достигает в точках х = -3 и х = 3), а 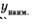 = 3 (этого значения функция достигает в точке х = 0. = 3 (этого значения функция достигает в точке х = 0.
В 7-м и 8-м классах мы упоминали еще два свойства функций. Первое назвали свойством выпуклости функции. Считается, что функция выпукла вниз на промежутке X, если, соединив любые две точки ее графика (с абсциссами из X) отрезком прямой, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 59). непрерывность Функция выпукла вверх на промежутке X, если, функции соединив любые две точки ее графика (с абсциссами из X) отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка (рис. 60).
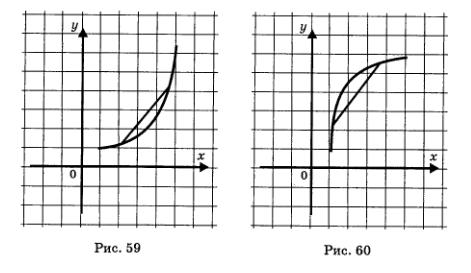
Второе свойство — непрерывность функции на промежутке X — означает, что график функции на промежутке X — сплошной, т.е. не имеет проколов и скачков.
Замечание.
На самом деле в математике все обстоит, как говорится, «с точностью до наоборот»: график функции изображается в виде сплошной линии (без проколов и скачков) только тогда, когда доказана непрерывность функции. Но формальное определение непрерывности функции, достаточно сложное и тонкое, нам пока не по силам. То же самое можно сказать и о выпуклости функции. Обсуждая указанные два свойства функций, будем по-прежнему опираться на наглядно-интуитивные представления.
А теперь проведем смотр наших знаний. Вспомнив о тех функциях, которые мы с вами изучали в 7-м и 8-м классах, уточним, как выглядят их графики, и перечислим свойства функции, придерживаясь определенного порядка, например такого: область определения; монотонность; ограниченность;  , ,  ; непрерывность; область значений; выпуклость. ; непрерывность; область значений; выпуклость.
Впоследствии появятся новые свойства функций, соответственно будет меняться и перечень свойств.
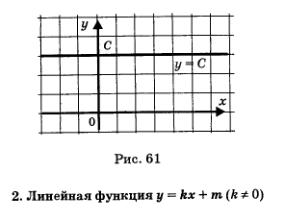
1. Постоянная функция у = С
График функции у = С изображен на рис. 61 — прямая, параллельная оси х. Это настолько неинтересная функция, что нет смысла перечислять ее свойства.
Графиком функции у = кх + m является прямая (рис. 62, 63).
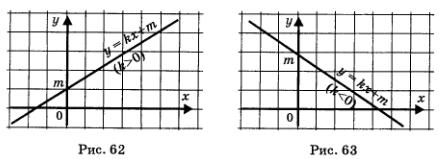
Свойства функции у = кх + m:
1) 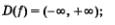
2) возрастает, если к > 0 (рис. 62), убывает, если к < 0 (рис. 63);
3) не ограничена ни снизу, ни сверху;
4) нет ни наибольшего, ни наименьшего значений;
5) функция непрерывна;
6) 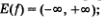
7) о выпуклости говорить не имеет смысла.
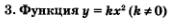
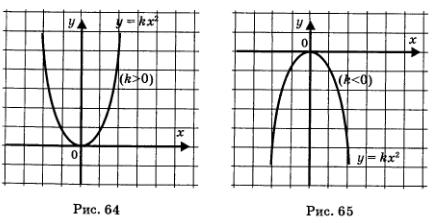
Графиком функции у = кх2 является парабола с вершиной в начале координат и с ветвями, направленными вверх, если к > О (рис. 64), и вниз, если к < 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.
Свойства функции у - кх2:
Для случая к> 0 (рис. 64):
1) D(f) = (-оо,+оо);
2) убывает на луче (-оо, 0], возрастает на луче [0, +оо);
3) ограничена снизу, не ограничена сверху;
4)  = =  не существует; не существует;
5) непрерывна;
6) Е(f) = [0,+оо);
7) выпукла вниз.
Обратите внимание: на промежутке (-оо, 0] функция убывает, а на промежутке [0, +оо) функция возрастает. Эти промежутки называют промежутками монотонности функции у = кх2. Понятие промежутка монотонности будем использовать и для других функций.
Для случая к < 0 (рис. 65):
1) D(f) = (-оо,+00);
2) возрастает на луче (-оо, 0], убывает на луче [0, +оо);
3) не ограничена снизу, ограничена сверху;
4)  не существует, не существует,  = 0; = 0;
5) непрерывна;
6) Е(f) > = (-оо, 0];
7) выпукла вверх.
График функции у = f(х) строится по точкам; чем больше точек вида (х; f(х)) мы возьмем, тем более точное представление о графике получим. Если этих точек взять достаточно много, то и представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает нам, что график надо изобразить в виде сплошной линии (в данном случае в виде параболы). А уж затем, читая график, мы делаем выводы о непрерывности функции, о ее выпуклости вниз или вверх, об области значений функции. Вы должны понимать, что из перечисленных семи свойств «законными» являются лишь свойства 1), 2), 3), 4) — «законными» в том смысле, что мы в состоянии обосновать их, ссылаясь на точные определения. Об остальных свойствах у нас имеются только наглядно-интуитивные представления. Кстати, в этом нет ничего плохого. Из истории развития математики известно, что человечество часто и долго пользовалось различными свойствами тех или иных объектов, не зная точных определений. Потом, когда такие определения удавалось сформулировать, все становилось на свои места.
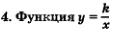
Графиком функции является гипербола, оси координат служат асимптотами гиперболы (рис. 66, 67).
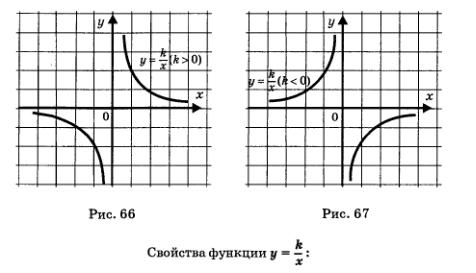
1) D(f) = (-00,0)1U (0,+оо);
2) если к > 0, то функция убывает на открытом луче (-оо, 0) и на открытом луче (0, +оо) (рис. 66); если к < 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) не ограничена ни снизу, ни сверху;
4) нет ни наименьшего, ни наибольшего значений;
5) функция непрерывна на открытом луче (-оо, 0) и на открытом луче (0, +оо);
6) Е(f) = (-оо,0) U (0,+оо);
7) если к > 0, то функция выпукла вверх при х < 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х > 0, т.е. на открытом луче (0, +оо) (рис. 66). Если к < 0, то функция выпукла вверх при х > О и выпукла вниз при х < О (рис. 67).
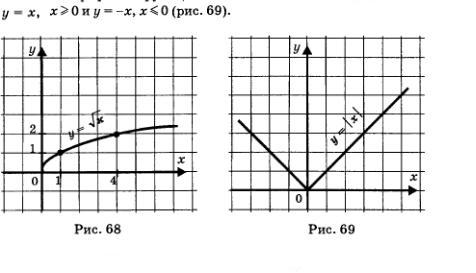
5. Функция 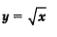
Графиком функции является ветвь параболы (рис. 68). Свойства функции 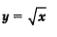 : :
1) D(f) = [0, +оо);
2) возрастает;
3) ограничена снизу, не ограничена сверху;
4)  = =  не существует; не существует;
5) непрерывна;
6) Е(f) = [0,+оо);
7) выпукла вверх.
6. Функция у = | х |
Графиком функции является объединение двух лучей:
Свойства функции у= | х |:
1) D(f) = (-оо,+оо);
2) убывает на луче (-оо, 0], возрастает на луче [0, +оо);
3) ограничена снизу, не ограничена сверху;
4) 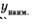 = = не существует; не существует;
5) непрерывна;
6) Е(f) = [0,+оо);
7) функцию можно считать выпуклой вниз.
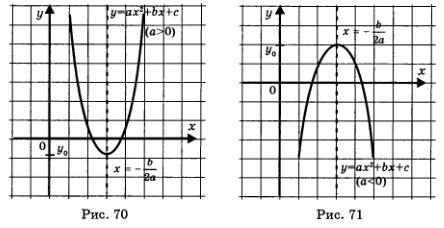
7. Функция у = ах2 + Ьх + с
Графиком функции является парабола с вершиной в точке 
и с ветвями, направленными вверх, если а > 0 (рис. 70), и вниз,
если а < 0 (рис. 71). Прямая 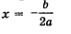 является осью параболы. является осью параболы.
Смотр наших знаний о функциях можно считать законченным. Разумеется, приведенным перечнем в реальной жизни не обойтись. Некоторые новые функции и их свойства встретятся нам уже в этой главе.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|