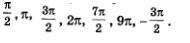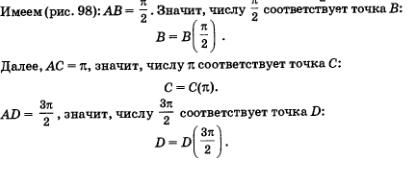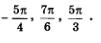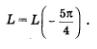|
|
|
| (7 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Числовая окружность<metakeywords>Числовая окружность</metakeywords>''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Числовая окружность<metakeywords>Числовая окружность, математические модели, числовая окружность, числовой прямой, положительному числу, точку, математического языка, числу</metakeywords>''' |
| | | | |
| | + | <br> |
| | | | |
| | + | '''Числовая окружность''' |
| | | | |
| - | '''ЧИСЛОВАЯ ОКРУЖНОСТЬ'''<br>Изучая курс алгебры 7—9-го классов, мы до сих пор имели дело с алгебраическими функциями, т.е. функциями, заданными аналитически выражениями, в записи которых использовались алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение квадратного корня). Но математические модели реальных ситуаций часто бывают связаны с функциями другого типа, не алгебраическими. С первыми представителями класса неалгебраических функций — тригонометрическими функциями — мы познакомимся в этой главе. Более детально изучать тригонометрические функции и другие виды неалгебраических функций (показательные и логарифмические) вам предстоит в старших классах.<br>Для введения тригонометрических функций нам понадобится новая математическая модель — числовая окружность, с которой вы до сих пор не встречались, зато хорошо знакомы с числовой прямой. Напомним, что числовая прямая — это прямая, на которой заданы начальная точка О, масштаб (единичный отрезок) и положительное направление. Любое действительное число мы можем сопоставить с точкой на прямой и обратно.<br><br>втрое<br>вопрос<br>1<br>)<br>)<br>Как по числу х найти на прямой соответствующую точку М? Числу 0 соответствует начальная точка О. Если х > 0, то, двигаясь по прямой из точки 0 в положительном направлении, нужно пройти п^ть длиной х; конец этого пути и будет искомой точкой М(х). Если х < 0, то, двигаясь по прямой из точки О в отрицательном направлении, нужно пройти путь 1*1; конец этого пути и будет искомой точкой М(х). Число х — координата точки М.<br>А как мы решали обратную задачу, т.е. как искали координату х заданной точки М на числовой прямой? Находили длину отрезка ОМ и брали ее со знаком «+» или * — » в зависимости от того, с какой стороны от точки О расположена на прямой точка М.<br>Но в реальной жизни двигаться приходится не только по прямой. Довольно часто рассматривается движение по окружности. Вот конкретный пример. Будем считать беговую дорожку стадиона окружностью (на самом деле это, конечно, не окружность, но вспомните, как обычно говорят спортивные комментаторы: «бегун пробежал круг», «до финиша осталось пробежать полкруга» и т.д.), ее длина равна 400 м. Отмечен старт — точка А (рис. 97). Бегун из точки А движется по окружности против часовой стрелки. Где он будет через 200 м? через 400 м? через 800 м? через 1500 м? А где провести финишную черту, если он бежит марафонскую дистанцию 42 км 195 м?<br> <br> в <br> •X <br> м \ <br> с А <br> О <br> V <br> \ N <br> <br> <br>Рис. 126<br>146<br>518.Ц ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>Через 200 м он будет находиться в точке С, диаметрально противоположной точке А (200 м — это длина половины беговой дорожки, т.е. длина половины окружности). Пробежав 400 м (т.е. «один круг», как говорят спортсмены), он вернется в точку А. Про-беЦав 800 м (т.е. «два круга»), он вновь окажется в точке А. А что такое 1500 м? Это «три круга» (1200 м) плюс еще 300 м, т.е. 3<br>— беговой дорожки — финиш этой дистанции будет в точке 2) (рис. 97).<br>Нам осталось разобраться с марафоном. Пробежав 105 кругов, спортсмен преодолеет путь 105-400 = 42 000 м, т.е. 42 км. До финиша остается 195 м, это на 5 м меньше половины длины окружности. Значит, финиш марафонской дистанции будет в точке М, расположенной около точки С (рис. 97).<br>Замечание. Вы, разумеется, понимаете условность последнего примера. Марафонскую дистанцию по стадиону никто не бегает, максимум составляет 10 000 м, т.е. 25 кругов.<br>По беговой дорожке стадиона можно пробежать или пройти путь любой длины. Значит, любому положительному числу соответствует какая-то точка — «финиш дистанции». Более того, можно и любому отрицательному числу поставить в соответствие точку окружности: просто надо заставить спортсмена бежать в противоположном направлении, т.е. стартовать из точки А не в направлении против,ав направлении по часовой стрелке. Тогда беговую дорожку стадиона можно рассматривать как числовую окружность.<br>В принципе, любую окружность можно рассматривать как числовую, но в математике условились использовать для этой цели единичную окружность — окружность с радиусом 1. Это будет наша «беговая дорожка». Длина Ь окружности с радиусом К вычисляется по формуле Ь = 2лК, где л ~ 3,14. Если К = 1, то Ь = 2л ~ 6,28. Длина половины окружности равна л, а длина четверти окружно-<br>71<br>сти — АВ, ВС, СБ, 1)А на рис. 98 — равна -. Условимся называть<br>дугу АВ первой четвертью единичной окружности, дугу ВС — второй четвертью, дугу С1) — третьей четвертью, дугу ДА —<br>10*<br>147<br>5.17.||<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>четвертой четвертью (рис. 98). При этом обычно речь идет об Открытой дуге, т.е. о дуге без ее концов (что-то вроде интервала на числовой прямой). I<br> <br> в <br> II I <br> <br> С А <br> О <br> \ <br> И? ч IV <br> в <br> <br>Рис. 98<br>Определение. Дана единичная окружность, на ней отмечена начальная точка А — правый конец горизонтального диаметра (рис. 98). Поставим в соответствие каждому действительному числу I точку окружности по следующему правилу:<br>1) если * > 0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь длиной и конечная точка М этого пути и будет искомой точкой: М = М(*);<br>2) если ^ < 0, то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь длиной и |; конечная точка М этого пути и будет искомой точкой: М = М(1);<br>= 0 поставим в соответствие точку А: А = А(0).<br>Единичную окружность с установленным соответствием (между действительными числами и точками окружности) будем называть числовой окружностью.<br>Пример 1. Найти на числовой окружности<br>л<br>точку, которая соответствует заданному числу: —, п,<br>Зл 7л Зл<br>о > 2л, „ , 9л,— 0 .<br>3)числу *<br><br>числовая окружность<br>148<br>5.17.||<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>Решение. Так как первые шесть из заданных семи чисел положительны, то для отыскания соответствующих им точек на окружности нужно пройти по окружности путь заданной длины, двигаясь из точки А в положительном направлении. Учтем при этом, что<br>л<br>длина каждой четверти единичнои окружности равна -.<br>л л &<br>Имеем (рис. 98): АВ = -. Значит, числу - соответствует точка В: а / 2<br>л л<br>в"в[к<br>Далее, АС = л, значит, числу л соответствует точка С:<br>С = С(л).<br>л Зл Зл _<br>АО = ~, значит, числу — соответствует точка V:<br>1> = 1)<br>Зл 2<br>\<br>Числу 2л соответствует точка А, так как, пройдя по окружности путь длиной 2л, т.е. ровно одну окружность, мы снова попадем в начальную точку А Итак, А = А(2л). 7л Зл<br>Что такое — ? Это 2л 4- — . Значит, двигаясь из точки А в положительном направлении, нужно пройти целую окружность (путь<br>Зл<br>длиной 2л) и еще путь длиной , который, как мы видели выше,<br>С 7лч<br>закончится в точке В. Итак, В = 1)1<br>Что такое 9т:? Это 4 • 2л + л. Значит, двигаясь из точки А в положительном направлении, нужно четыре раза описать целую окружность (путь длиной 4-2п) и еще путь длиной л, который, как мы видели выше, закончится в точке С. Итак, С — С(9л).<br>Осталось найти на числовой окружности точку, соответствую-<br>Зл _<br>щую заданному отрицательному числу - — . Для этого нужно, от-<br>правляясь из точки А, пройти по окружности в отрицатель-<br>„ Зл .<br>ном направлении путь длинои — . Этот путь завершится<br>вточкеВ.Итак,В = В^~у|. <1<br>Замечание. Когда мы в 7—8-м классах работали с числовой прямой, то условились, ради краткости, не говорить «точка прямой, соответствующая числу х»,<br>149<br>5.17.<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>а говорить «точка х». Точно такой же договоренности будем придерживаться и при работе с числовой окружностью: «точка /» — это значит, что речь идет о точке окружности, которая соответствует числу<br>Пример 2. Найти на числовой окружности точки, соответ-<br>п Я 11 ствующие числам -, - , ^ .<br>Решение. Разделив первую четверть АВ на три равные час-<br>ти точками К и Р, получим: К = К\~<br>,Р = Р<br>АВ пополам точкой М, получим: М = М\ т (рис. 99). <11<br>. Разделив дугу<br> В <br> 1 М <br> 7<br> <br>С \ А <br> 0 <br> <br> Л <br> о ^8 <br> <br>Рис. 99<br>Пример 3. Найти на числовой окружности точки, соответствующие числам _ , — , ЁЕ .<br>4 6 3<br>Решение. Построения будем делать, пользуясь рис. 99.<br>71<br>Отложив дугу АМ (ее длина равна —) от точки А пять раз в отрицательном направлении, получим точку!, — середину дуги ВС. Итак,<br>Ь^Ь<br>5я<br>т<br>150<br>5.17.||<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>я<br>Отложив дугу АК (ее длина равна —) от точки А семь раз в положительном направлении, попадем в точку Ы, которая принадлежит<br>я<br>третьей четверти — дуге СБ, причем СЫ = ~ (третья часть дуги (ь СБ). Итак, N = N у .<br>V / л<br>Отложив дугу АК (ее длина равна — ) от точки А десять раз в<br>положительном направлении, попадем в точку 8, которая принад-<br>я<br>лежит четвертой четверти — дуге БА, причем Б8 = ~ (третья часть<br>дуги БА). Итак, 8 = 8<br>10я | Г 5я<br>т Мт<br>Заме чание. Обратите внимание на некоторую вольность, которую мы позволяем себе в использовании математического языка. Ясно, что дуга АК и д л и -на дуги АК — разные вещи (первое понятие — геометрическая фигура, а второе понятие — число). Но обозначается и то и другое одинаково: АК. Более того, если точки А и К соединить отрезком, то и полученный отрезок, и его длина обозначаются так же: АК. Обычно из контекста бывает ясно, какой смысл вкладывается в обозначение (дуга, длина дуги, отрезок или длина отрезка).<br>Особенно часто приходится искать на числовой окружности точ-<br>я я я я 5я<br>ки, соответствующие числам —, 7, -т, - и их кратным (т.е. —, олп 0 4 6 1 6<br>Зя 2я 9я . __<br>—, —, — и т.д.). Поэтому нам очень пригодятся два макета чис-4 3 2 ловой окружности.<br>ПЕРВЫЙ МАКЕТ<br>Каждая из четырех четвертей числовой окружности разделена на две равные части, и около каждой из имеющихся восьми точек записаны их «имена» (рис. 100).<br>ВТОРОЙ МАКЕТ Каждая из четырех четвертей числовой окружности разделена на три равные части, и около каждой из имеющихся двенадцати точек записаны их «имена» (рис. 101).<br><br>151<br>Учтите, что на обоих макетах мы могли бы заданным точкам<br>присвоить и другие «имена». Так, числу - — соответствует середина<br>4<br>четвертой четверти. Этой точке на первом макете присвоено «имя»<br>7Я п ТУ «<br>~г , но, как видите, мы могли присвоить ей и «имя» -—. Вообще, 4 4<br>если двигаться по первому макету из точки 0 по часовой стрелке, получим для имеющихся на чертеже восьми точек соответственно<br>л л Зп 5л Зл 7л .<br>О, - -, - —, - — , -я, - — — — . Аналогично, если двигать-<br>4 2 4 4 2 4<br>ся по второму макету из точки 0 по часовой стрелке, получим для<br>Л Л<br>имеющихся на чертеже двенадцати точек соответственно 0, - —,<br>6<br>л я 2л 5л 11л<br>~ 3 ' ~ 2 ' ~ ~3 ' ~ Т ' '"' ~ "б" '<br>Заметили ли вы, что во всех разобранных примерах длины дуг<br>выражались некоторыми долями числа п? Это неудивительно: ведь длина единичной окружности равна 2п, и если мы окружность или ее четверть делим на равные части, то получаются дуги, длины которых выражаются долями числа и. А как вы думаете, можно ли найти на единичной окружности такую точку Е, что длина дуги АЕ будет равна 1? Давайте прикинем:<br>л 3,14 л 3,14<br>я» 3,14; з--^- «1,047; » 0,786.<br>152<br>5.17.||<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>Таким образом,<br>Обратимся снова к рис. 99. Точка Е, такая, что АЕ = 1, находится между точками М и Р, поближе к точке Р. Разумеется, точно (а не приблизительно) указать положение точки Е на окружности мы не сумеем, но это, впрочем, не так уж важно.<br>Рассуждая аналогичным образом, делаем вывод, что на единичной окружности можно найти и точку Ег, для которой АЕ, = 1, и точку Е2, для которой АЕг = 2, и точку Е3, для которой АЕ3 = 3, и точку Е4, для которой АЕ4 = 4, и точку Еь, для которой АЕЪ = 5, и точку Е6, для которой АЕ6 = 6. На рис. 102 отмечены (приблизительно) соответствующие точки (причем для ориентировки каждая из четвертей единичной окружности разделена черточками на три равные части).<br>Рис. 102<br>Пример 4. Найти на числовой окружности точку, соответствующую числу -7.<br>Решение. Нам нужно, отправляясь из точки А(0) и двигаясь в отрицательном направлении (в направлении по часовой стрелке), пройти по окружности путь длиной 7. Если пройти одну окружность, то получим (приближенно) 6,28, значит, нужно еще пройти (в том же направлении) путь длиной 0,72. Что же это за дуга? Немного меньше половины четверти окружности, т.е. ее длина<br>153<br>5.17.||<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>меньше числа —. Почему? Да потому, что 3,14, а - =0,785; ясно, что 0,72 < 0,785. ТочкаМ = М(-7) отмечена на рис. 103 (мы немного не дошли до середины четвертой четверти). (И<br> Iв <br> <br> <br> <br>С о А<br> <br> <br> (-7)<br> Б <br> <br>Рис. 103<br>Итак, начисловой окружности, как и начисловой прямой, каждому действительному числу соответствует одна точка (только, разумеется, на прямой ее найти легче, чем на окружности). Но для прямой верно и обратное: каждая точка соответствует единственному числу. Для числовой окружности такое утверждение неверно, выше мы неоднократно убеждались в этом. Для числовой окружности справедливо следующее утверждение.<br>Если точка М числовой окружности соответствует числу I, то она соответствует и числу вида I + 2як, где к — любое целое число (к е 2).<br>В самом деле, 2п — длина числовой (единичной) окружности, а целое число |й| можно рассматривать как количество полных обходов окружности в ту или другую сторону. Если, например, к = 3, то это значит, что мы делаем три обхода окружности в положительном направлении; если к = -7, то это значит, что мы делаем семь (| к | = | -71 = 7) обходов окружности в отрицательном направлении. Но если мы находимся в точке М(1), то, выполнив еще | к | полных обходов окружности, мы снова окажемся в точке М. Итак,<br>154<br>5.17.||<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>М(1) = М(1 + 2яй).)<br>На двух макетах числовой окружности (рис. 100,101) указаны лишь главные «имена» точек — числа, принадлежащие отрезку [0, 2л], т.е. числа, возникающие при первом обходе окружности в<br>я<br>положительном направлении. На самом деле у точки — бесконеч-<br>я 5я<br>но много «имен»: I = — + 2пк, где ке2; у точки у тоже бесконечно<br>5я<br>много «имен»: I = — + 2пк, где к е 2, и т.д.<br>Число к обычно называют параметром. Впрочем, параметр можно обозначить и другой буквой, например п или т.<br>Замечание. Условимся в дальнейшем не писать каж-параметр дый раз: ке 2 или пе 2 (но, естественно, мы все время<br>будем это подразумевать).<br>Пример 5. Найти на числовой окружности точку: 19я 37я<br>а)-г; б)<br>4 ' ' 6 Р е ш е н и е. а) Имеем<br>19я 4<br>19<br>я =<br>4 + -4<br>Зя Зя я = 4л+ — = -г +2п-2. 4 4<br>19я<br>Значит, числу —— соответствует на числовой окружности та же<br>Зя<br>точка, что и числу — кет — рис. 100). б) Имеем<br>середина второй четверти (см. первый ма-<br>37я 37 („ 1<br>- = -—я = - 6 + -<br>6 6^6<br>37<br>я я ■ тс = -6я- - =-- +2п-(-3).<br>6 6 4 '<br>Значит, числу - соответствует на числовой окружности та же<br>точка, что и числу (рис. 101). <1<br>■ — , — это точка о<br>11я<br>на втором макете<br>155<br>5.17.||<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
| + | <br>Изучая [http://xvatit.com/vuzi/ курс] алгебры 7—9-го классов, мы до сих пор имели дело с алгебраическими функциями, т.е. функциями, заданными аналитически выражениями, в записи которых использовались алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение квадратного корня). Но [[Что такое математическая модель|математические модели]] реальных ситуаций часто бывают связаны с функциями другого типа, не алгебраическими. С первыми представителями класса неалгебраических функций — тригонометрическими функциями — мы познакомимся в этой главе. Более детально изучать тригонометрические функции и другие виды неалгебраических функций (показательные и логарифмические) вам предстоит в старших классах. |
| | | | |
| - | А.Г. Мордкович Алгебра 9 класс | + | Для введения тригонометрических функций нам понадобится новая математическая модель — [[2. Числовая окружность|числовая окружность]], с которой вы до сих пор не встречались, зато хорошо знакомы с числовой прямой. Напомним, что числовая прямая — это прямая, на которой заданы начальная точка О, масштаб (единичный отрезок) и положительное направление. Любое действительное число мы можем сопоставить с точкой на прямой и обратно.<br>Как по числу х найти на прямой соответствующую точку М? Числу 0 соответствует начальная точка О. Если х > 0, то, двигаясь по прямой из точки 0 в положительном направлении, нужно пройти п^ть длиной х; конец этого пути и будет искомой точкой М(х). Если х < 0, то, двигаясь по прямой из точки О в отрицательном направлении, нужно пройти путь 1*1; конец этого пути и будет искомой точкой М(х). Число х — координата точки М. |
| | + | |
| | + | А как мы решали обратную задачу, т.е. как искали координату х заданной точки М на [[Числові проміжки. Об'еднання та переріз числових проміжків|числовой прямой]]? Находили длину отрезка ОМ и брали ее со знаком «+» или * — » в зависимости от того, с какой стороны от точки О расположена на прямой точка М. |
| | + | |
| | + | Но в реальной жизни двигаться приходится не только по прямой. Довольно часто рассматривается движение по окружности. Вот конкретный пример. Будем считать беговую дорожку стадиона окружностью (на самом деле это, конечно, не окружность, но вспомните, как обычно говорят спортивные комментаторы: «бегун пробежал круг», «до финиша осталось пробежать полкруга» и т.д.), ее длина равна 400 м. Отмечен старт — точка А (рис. 97). Бегун из точки А движется по окружности против часовой стрелки. Где он будет через 200 м? через 400 м? через 800 м? через 1500 м? А где провести финишную черту, если он бежит марафонскую дистанцию 42 км 195 м? |
| | + | |
| | + | [[Image:Alg11.jpg|240px|Числовая окружность]] |
| | + | |
| | + | Через 200 м он будет находиться в точке С, диаметрально противоположной точке А (200 м — это длина половины беговой дорожки, т.е. длина половины окружности). Пробежав 400 м (т.е. «один круг», как говорят спортсмены), он вернется в точку А. Пробежав 800 м (т.е. «два круга»), он вновь окажется в точке А. А что такое 1500 м? Это «три круга» (1200 м) плюс еще 300 м, т.е. 3 — беговой дорожки — финиш этой дистанции будет в точке 2) (рис. 97). |
| | + | |
| | + | Нам осталось разобраться с марафоном. Пробежав 105 кругов, спортсмен преодолеет путь 105-400 = 42 000 м, т.е. 42 км. До финиша остается 195 м, это на 5 м меньше половины длины окружности. Значит, финиш марафонской дистанции будет в точке М, расположенной около точки С (рис. 97). |
| | + | |
| | + | '''Замечание'''. Вы, разумеется, понимаете условность последнего примера. Марафонскую дистанцию по стадиону никто не бегает, максимум составляет 10 000 м, т.е. 25 кругов. |
| | + | |
| | + | По беговой дорожке стадиона можно пробежать или пройти путь любой длины. Значит, любому [[Презентація уроку на тему «Додатні та від'ємні числа. Число 0»|положительному числу]] соответствует какая-то точка — «финиш дистанции». Более того, можно и любому отрицательному числу поставить в соответствие точку окружности: просто надо заставить спортсмена бежать в противоположном направлении, т.е. стартовать из точки А не в направлении против,ав направлении по часовой стрелке. Тогда беговую дорожку стадиона можно рассматривать как числовую окружность. |
| | + | |
| | + | В принципе, любую окружность можно рассматривать как числовую, но в математике условились использовать для этой цели единичную окружность — окружность с радиусом 1. Это будет наша «беговая дорожка». Длина b окружности с радиусом К вычисляется по формуле[[Image:Alg12.jpg|360px|Формула]] Длина половины окружности равна n, а длина четверти окружности — АВ, ВС, СБ, DА на рис. 98 — равна[[Image:Alg13.jpg]] Условимся называть дугу АВ первой четвертью единичной окружности, дугу ВС — второй четвертью, дугу СB — третьей четвертью, дугу DА — четвертой четвертью (рис. 98). При этом обычно речь идет об Открытой дуге, т.е. о дуге без ее концов (что-то вроде интервала на числовой прямой). |
| | + | |
| | + | [[Image:Alg14.jpg|240px|Числовая окружность]] |
| | + | |
| | + | '''Определение.''' |
| | + | |
| | + | Дана единичная окружность, на ней отмечена начальная точка А — правый конец горизонтального диаметра (рис. 98). Поставим в соответствие каждому действительному числу I точку окружности по следующему правилу: |
| | + | |
| | + | 1) если x > 0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь длиной и конечная точка М этого пути и будет искомой точкой: М = М(x); |
| | + | |
| | + | 2) если x < 0, то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь длиной и |; конечная точка М этого пути и будет искомой точкой: М = М(1); = 0 поставим в соответствие [[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точку]] А: А = А(0). |
| | + | |
| | + | Единичную окружность с установленным соответствием (между действительными числами и точками окружности) будем называть числовой окружностью. |
| | + | |
| | + | '''Пример 1.''' |
| | + | |
| | + | Найти на числовой окружности [[Image:Alg15.jpg|240px|Заданиеп]] |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | Так как первые шесть из заданных семи чисел положительны, то для отыскания соответствующих им точек на окружности нужно пройти по окружности путь заданной длины, двигаясь из точки А в положительном направлении. Учтем при этом, что |
| | + | |
| | + | [[Image:Alg16.jpg|480px|Решение]] |
| | + | |
| | + | Числу 2[[Image:Alg17.jpg]] соответствует точка А, так как, пройдя по окружности путь длиной 2[[Image:Alg17.jpg]], т.е. ровно одну окружность, мы снова попадем в начальную точку А Итак, А = А(2[[Image:Alg17.jpg]]). |
| | + | |
| | + | Что такое [[Image:Alg18.jpg|120px|Формула]] Значит, двигаясь из точки А в положительном направлении, нужно пройти целую окружность. |
| | + | |
| | + | '''Замечание.''' |
| | + | |
| | + | Когда мы в 7—8-м классах работали с числовой прямой, то условились, ради краткости, не говорить «точка прямой, соответствующая числу х», а говорить «точка х». Точно такой же договоренности будем придерживаться и при работе с числовой окружностью: «точка f» — это значит, что речь идет о точке окружности, которая соответствует числу. |
| | + | |
| | + | <br>'''Пример 2.''' |
| | + | |
| | + | Найти на числовой окружности точки, соответствующие числам [[Image:Alg19.jpg|80px|Числа]]<br>'''Решение. ''' |
| | + | |
| | + | Разделив первую четверть АВ на три равные части точками К и Р, получим: |
| | + | |
| | + | <br>[[Image:Alg110.jpg|320px|Решение]]<br>'''Пример 3.''' |
| | + | |
| | + | Найти на числовой окружности точки, соответствующие числам [[Image:Alg111.jpg|120px|Числа]]<br>'''Решение.''' |
| | + | |
| | + | Построения будем делать, пользуясь рис. 99. Отложив дугу АМ (ее длина равна —) от точки А пять раз в отрицательном направлении, получим точку!, — середину дуги ВС. Итак,[[Image:Alg112.jpg|120px|Решение]]<br>'''Замечание. ''' |
| | + | |
| | + | Обратите внимание на некоторую вольность, которую мы позволяем себе в использовании [[Что такое математический язык|математического языка]]. Ясно, что дуга АК и д л ина дуги АК — разные вещи (первое понятие — геометрическая фигура, а второе понятие — число). Но обозначается и то и другое одинаково: АК. Более того, если точки А и К соединить отрезком, то и полученный отрезок, и его длина обозначаются так же: АК. Обычно из контекста бывает ясно, какой смысл вкладывается в обозначение (дуга, длина дуги, отрезок или длина отрезка). |
| | + | |
| | + | Поэтому нам очень пригодятся два макета числовой окружности. |
| | + | |
| | + | |
| | + | |
| | + | '''Первый макет''' |
| | + | |
| | + | Каждая из четырех четвертей числовой окружности разделена на две равные части, и около каждой из имеющихся восьми точек записаны их «имена» (рис. 100). |
| | + | |
| | + | '''Второй макет''' |
| | + | |
| | + | Каждая из четырех четвертей числовой окружности разделена на три равные части, и около каждой из имеющихся двенадцати точек записаны их «имена» (рис. 101). |
| | + | |
| | + | [[Image:Alg113.jpg|480px|Числовая окружность]]<br>Учтите, что на обоих макетах мы могли бы заданным точкам присвоить и другие «имена».<br>Заметили ли вы, что во всех разобранных примерах длины дуг выражались некоторыми долями числа n? Это неудивительно: ведь длина единичной окружности равна 2n, и если мы окружность или ее четверть делим на равные части, то получаются дуги, длины которых выражаются долями числа и. А как вы думаете, можно ли найти на единичной окружности такую точку Е, что длина дуги АЕ будет равна 1? Давайте прикинем: |
| | + | |
| | + | [[Image:Alg114.jpg|320px|Решение]]<br>Рассуждая аналогичным образом, делаем вывод, что на единичной окружности можно найти и точку Еu, для которой АЕ, = 1, и точку Е2, для которой АЕг = 2, и точку Е3, для которой АЕ3 = 3, и точку Е4, для которой АЕ4 = 4, и точку Еь, для которой АЕЪ = 5, и точку Е6, для которой АЕ6 = 6. На рис. 102 отмечены (приблизительно) соответствующие точки (причем для ориентировки каждая из четвертей единичной окружности разделена черточками на три равные части). |
| | + | |
| | + | [[Image:Alg115.jpg|240px|Числовая окружность]] |
| | + | |
| | + | <br>'''Пример 4.''' |
| | + | |
| | + | Найти на числовой окружности точку, соответствующую числу -7. |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | Нам нужно, отправляясь из точки А(0) и двигаясь в отрицательном направлении (в направлении по часовой стрелке), пройти по окружности путь длиной 7. Если пройти одну окружность, то получим (приближенно) 6,28, значит, нужно еще пройти (в том же направлении) путь длиной 0,72. Что же это за дуга? Немного меньше половины четверти окружности, т.е. ее длина меньше числа —. |
| | + | |
| | + | [[Image:Alg116.jpg|240px|Числовая окружность]] |
| | + | |
| | + | Итак, на числовой окружности, как и на числовой прямой, каждому действительному [[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|числу]] соответствует одна точка (только, разумеется, на прямой ее найти легче, чем на окружности). Но для прямой верно и обратное: каждая точка соответствует единственному числу. Для числовой окружности такое утверждение неверно, выше мы неоднократно убеждались в этом. Для числовой окружности справедливо следующее утверждение. |
| | + | |
| | + | Если точка М числовой окружности соответствует числу I, то она соответствует и числу вида I + 2як, где к — любое целое число (к е 2). |
| | + | |
| | + | В самом деле, 2п — длина числовой (единичной) окружности, а целое число |й| можно рассматривать как количество полных обходов окружности в ту или другую сторону. Если, например, к = 3, то это значит, что мы делаем три обхода окружности в положительном направлении; если к = -7, то это значит, что мы делаем семь (| к | = | -71 = 7) обходов окружности в отрицательном направлении. Но если мы находимся в точке М(1), то, выполнив еще | к | полных обходов окружности, мы снова окажемся в точке М. <br> |
| | + | |
| | + | |
| | + | ''А.Г. Мордкович Алгебра 9 класс'' |
| | | | |
| | <br> | | <br> |
| Строка 12: |
Строка 111: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 18:48, 10 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Числовая окружность
Числовая окружность
Изучая курс алгебры 7—9-го классов, мы до сих пор имели дело с алгебраическими функциями, т.е. функциями, заданными аналитически выражениями, в записи которых использовались алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение квадратного корня). Но математические модели реальных ситуаций часто бывают связаны с функциями другого типа, не алгебраическими. С первыми представителями класса неалгебраических функций — тригонометрическими функциями — мы познакомимся в этой главе. Более детально изучать тригонометрические функции и другие виды неалгебраических функций (показательные и логарифмические) вам предстоит в старших классах.
Для введения тригонометрических функций нам понадобится новая математическая модель — числовая окружность, с которой вы до сих пор не встречались, зато хорошо знакомы с числовой прямой. Напомним, что числовая прямая — это прямая, на которой заданы начальная точка О, масштаб (единичный отрезок) и положительное направление. Любое действительное число мы можем сопоставить с точкой на прямой и обратно.
Как по числу х найти на прямой соответствующую точку М? Числу 0 соответствует начальная точка О. Если х > 0, то, двигаясь по прямой из точки 0 в положительном направлении, нужно пройти п^ть длиной х; конец этого пути и будет искомой точкой М(х). Если х < 0, то, двигаясь по прямой из точки О в отрицательном направлении, нужно пройти путь 1*1; конец этого пути и будет искомой точкой М(х). Число х — координата точки М.
А как мы решали обратную задачу, т.е. как искали координату х заданной точки М на числовой прямой? Находили длину отрезка ОМ и брали ее со знаком «+» или * — » в зависимости от того, с какой стороны от точки О расположена на прямой точка М.
Но в реальной жизни двигаться приходится не только по прямой. Довольно часто рассматривается движение по окружности. Вот конкретный пример. Будем считать беговую дорожку стадиона окружностью (на самом деле это, конечно, не окружность, но вспомните, как обычно говорят спортивные комментаторы: «бегун пробежал круг», «до финиша осталось пробежать полкруга» и т.д.), ее длина равна 400 м. Отмечен старт — точка А (рис. 97). Бегун из точки А движется по окружности против часовой стрелки. Где он будет через 200 м? через 400 м? через 800 м? через 1500 м? А где провести финишную черту, если он бежит марафонскую дистанцию 42 км 195 м?
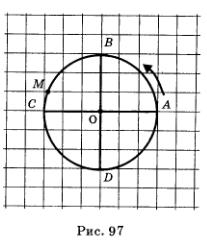
Через 200 м он будет находиться в точке С, диаметрально противоположной точке А (200 м — это длина половины беговой дорожки, т.е. длина половины окружности). Пробежав 400 м (т.е. «один круг», как говорят спортсмены), он вернется в точку А. Пробежав 800 м (т.е. «два круга»), он вновь окажется в точке А. А что такое 1500 м? Это «три круга» (1200 м) плюс еще 300 м, т.е. 3 — беговой дорожки — финиш этой дистанции будет в точке 2) (рис. 97).
Нам осталось разобраться с марафоном. Пробежав 105 кругов, спортсмен преодолеет путь 105-400 = 42 000 м, т.е. 42 км. До финиша остается 195 м, это на 5 м меньше половины длины окружности. Значит, финиш марафонской дистанции будет в точке М, расположенной около точки С (рис. 97).
Замечание. Вы, разумеется, понимаете условность последнего примера. Марафонскую дистанцию по стадиону никто не бегает, максимум составляет 10 000 м, т.е. 25 кругов.
По беговой дорожке стадиона можно пробежать или пройти путь любой длины. Значит, любому положительному числу соответствует какая-то точка — «финиш дистанции». Более того, можно и любому отрицательному числу поставить в соответствие точку окружности: просто надо заставить спортсмена бежать в противоположном направлении, т.е. стартовать из точки А не в направлении против,ав направлении по часовой стрелке. Тогда беговую дорожку стадиона можно рассматривать как числовую окружность.
В принципе, любую окружность можно рассматривать как числовую, но в математике условились использовать для этой цели единичную окружность — окружность с радиусом 1. Это будет наша «беговая дорожка». Длина b окружности с радиусом К вычисляется по формуле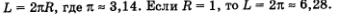 Длина половины окружности равна n, а длина четверти окружности — АВ, ВС, СБ, DА на рис. 98 — равна Длина половины окружности равна n, а длина четверти окружности — АВ, ВС, СБ, DА на рис. 98 — равна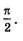 Условимся называть дугу АВ первой четвертью единичной окружности, дугу ВС — второй четвертью, дугу СB — третьей четвертью, дугу DА — четвертой четвертью (рис. 98). При этом обычно речь идет об Открытой дуге, т.е. о дуге без ее концов (что-то вроде интервала на числовой прямой). Условимся называть дугу АВ первой четвертью единичной окружности, дугу ВС — второй четвертью, дугу СB — третьей четвертью, дугу DА — четвертой четвертью (рис. 98). При этом обычно речь идет об Открытой дуге, т.е. о дуге без ее концов (что-то вроде интервала на числовой прямой).
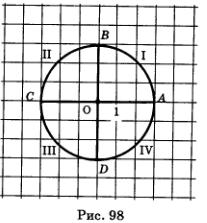
Определение.
Дана единичная окружность, на ней отмечена начальная точка А — правый конец горизонтального диаметра (рис. 98). Поставим в соответствие каждому действительному числу I точку окружности по следующему правилу:
1) если x > 0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь длиной и конечная точка М этого пути и будет искомой точкой: М = М(x);
2) если x < 0, то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь длиной и |; конечная точка М этого пути и будет искомой точкой: М = М(1); = 0 поставим в соответствие точку А: А = А(0).
Единичную окружность с установленным соответствием (между действительными числами и точками окружности) будем называть числовой окружностью.
Пример 1.
Найти на числовой окружности 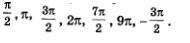
Решение.
Так как первые шесть из заданных семи чисел положительны, то для отыскания соответствующих им точек на окружности нужно пройти по окружности путь заданной длины, двигаясь из точки А в положительном направлении. Учтем при этом, что
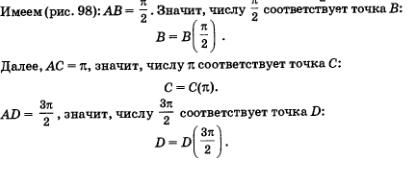
Числу 2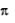 соответствует точка А, так как, пройдя по окружности путь длиной 2 соответствует точка А, так как, пройдя по окружности путь длиной 2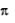 , т.е. ровно одну окружность, мы снова попадем в начальную точку А Итак, А = А(2 , т.е. ровно одну окружность, мы снова попадем в начальную точку А Итак, А = А(2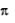 ). ).
Что такое 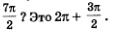 Значит, двигаясь из точки А в положительном направлении, нужно пройти целую окружность. Значит, двигаясь из точки А в положительном направлении, нужно пройти целую окружность.
Замечание.
Когда мы в 7—8-м классах работали с числовой прямой, то условились, ради краткости, не говорить «точка прямой, соответствующая числу х», а говорить «точка х». Точно такой же договоренности будем придерживаться и при работе с числовой окружностью: «точка f» — это значит, что речь идет о точке окружности, которая соответствует числу.
Пример 2.
Найти на числовой окружности точки, соответствующие числам 
Решение.
Разделив первую четверть АВ на три равные части точками К и Р, получим:

Пример 3.
Найти на числовой окружности точки, соответствующие числам 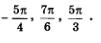
Решение.
Построения будем делать, пользуясь рис. 99. Отложив дугу АМ (ее длина равна —) от точки А пять раз в отрицательном направлении, получим точку!, — середину дуги ВС. Итак,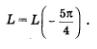
Замечание.
Обратите внимание на некоторую вольность, которую мы позволяем себе в использовании математического языка. Ясно, что дуга АК и д л ина дуги АК — разные вещи (первое понятие — геометрическая фигура, а второе понятие — число). Но обозначается и то и другое одинаково: АК. Более того, если точки А и К соединить отрезком, то и полученный отрезок, и его длина обозначаются так же: АК. Обычно из контекста бывает ясно, какой смысл вкладывается в обозначение (дуга, длина дуги, отрезок или длина отрезка).
Поэтому нам очень пригодятся два макета числовой окружности.
Первый макет
Каждая из четырех четвертей числовой окружности разделена на две равные части, и около каждой из имеющихся восьми точек записаны их «имена» (рис. 100).
Второй макет
Каждая из четырех четвертей числовой окружности разделена на три равные части, и около каждой из имеющихся двенадцати точек записаны их «имена» (рис. 101).
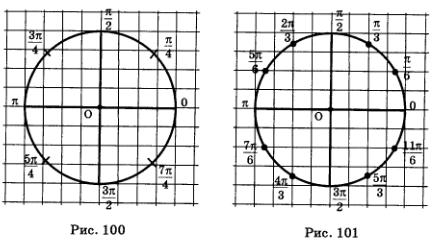
Учтите, что на обоих макетах мы могли бы заданным точкам присвоить и другие «имена».
Заметили ли вы, что во всех разобранных примерах длины дуг выражались некоторыми долями числа n? Это неудивительно: ведь длина единичной окружности равна 2n, и если мы окружность или ее четверть делим на равные части, то получаются дуги, длины которых выражаются долями числа и. А как вы думаете, можно ли найти на единичной окружности такую точку Е, что длина дуги АЕ будет равна 1? Давайте прикинем:
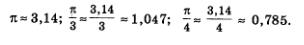
Рассуждая аналогичным образом, делаем вывод, что на единичной окружности можно найти и точку Еu, для которой АЕ, = 1, и точку Е2, для которой АЕг = 2, и точку Е3, для которой АЕ3 = 3, и точку Е4, для которой АЕ4 = 4, и точку Еь, для которой АЕЪ = 5, и точку Е6, для которой АЕ6 = 6. На рис. 102 отмечены (приблизительно) соответствующие точки (причем для ориентировки каждая из четвертей единичной окружности разделена черточками на три равные части).
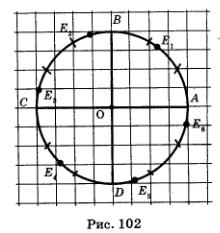
Пример 4.
Найти на числовой окружности точку, соответствующую числу -7.
Решение.
Нам нужно, отправляясь из точки А(0) и двигаясь в отрицательном направлении (в направлении по часовой стрелке), пройти по окружности путь длиной 7. Если пройти одну окружность, то получим (приближенно) 6,28, значит, нужно еще пройти (в том же направлении) путь длиной 0,72. Что же это за дуга? Немного меньше половины четверти окружности, т.е. ее длина меньше числа —.
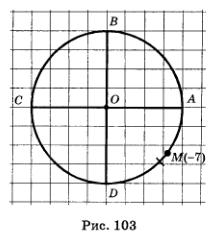
Итак, на числовой окружности, как и на числовой прямой, каждому действительному числу соответствует одна точка (только, разумеется, на прямой ее найти легче, чем на окружности). Но для прямой верно и обратное: каждая точка соответствует единственному числу. Для числовой окружности такое утверждение неверно, выше мы неоднократно убеждались в этом. Для числовой окружности справедливо следующее утверждение.
Если точка М числовой окружности соответствует числу I, то она соответствует и числу вида I + 2як, где к — любое целое число (к е 2).
В самом деле, 2п — длина числовой (единичной) окружности, а целое число |й| можно рассматривать как количество полных обходов окружности в ту или другую сторону. Если, например, к = 3, то это значит, что мы делаем три обхода окружности в положительном направлении; если к = -7, то это значит, что мы делаем семь (| к | = | -71 = 7) обходов окружности в отрицательном направлении. Но если мы находимся в точке М(1), то, выполнив еще | к | полных обходов окружности, мы снова окажемся в точке М.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|