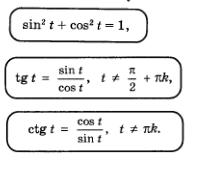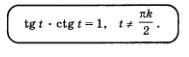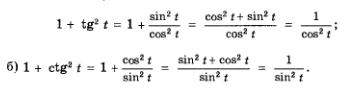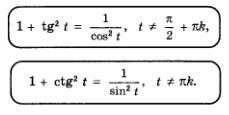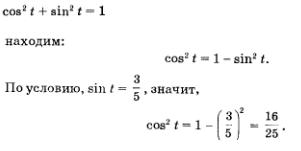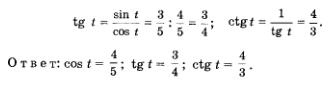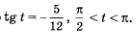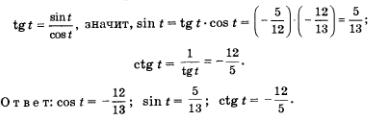|
|
|
| (2 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Тригонометрические функции числового аргумента''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Тригонометрические функции числового аргумента<metakeywords>Тригонометрические функции числового аргумента, число, координатной плоскости, функции, выражение, числовой окружности</metakeywords>'''<br> <br> |
| | | | |
| | + | '''Тригонометрические функции числового аргумента''' |
| | | | |
| | + | <br>Какое бы действительное число t ни взять, ему можно поставить в соответствие однозначно определенное [[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|число]] t. Правда, правило соответствия довольно сложное, оно, как мы видели выше, заключается в следующем. Чтобы, по числу t найти значение sin t, нужно: |
| | | | |
| - | ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА<br>Какое бы действительное число t ни взять, ему можно поставить в соответствие однозначно определенное число t. Правда, правило соответствия довольно сложное, оно, как мы видели выше, заключается в следующем.<br>Чтобы, по числу t найти значение sin t, нужно:<br>1) расположить числовую окружность в координатной плоскости так, чтобы центр окружности совпал с началом координат, а начальная точка А окружности попала в точку (1; 0);<br>2) на окружности найти точку, соответствующую числу 2;<br>3) найти ординату этой точки. Эта ордината и есть sin t.<br>Фактически речь идет о функции u = sin t, где 2 — любое действительное число. Вы умеете вычислять некоторые значения этой функции (например, [[Image:alg41.jpg]], знаете некоторые ее свойства.<br>Точно так же можно считать, что в предыдущем параграфе вы получили некоторые представления еще о трех функциях: [[Image:alg42.jpg]] Все эти функции называют тригонометрическими функциями числового аргумента t.<br>Есть целый ряд соотношений, связывающих значения различных тригонометрических функций, неметрические которые из этих соотношений вы уже знаете:
| + | 1) расположить числовую окружность в [[Ілюстрації до теми Координатна площина|координатной плоскости]] так, чтобы центр окружности совпал с началом координат, а начальная точка А окружности попала в точку (1; 0); |
| | | | |
| - | [[Image:alg43.jpg]] <br>Из двух последних формул легко получить соотношение, связывающее tg t и ctg t
| + | 2) на окружности найти точку, соответствующую числу 2; |
| | | | |
| - | [[Image:alg44.jpg]]<br>'''Пример 1.''' Упростить выражение:
| + | 3) найти ординату этой точки. Эта ордината и есть sin t. |
| | | | |
| - | [[Image:alg45.jpg]] | + | Фактически речь идет о функции u = sin t, где 2 — любое действительное число. Вы умеете вычислять некоторые значения этой функции (например, [[Image:Alg41.jpg|180px|Функции]], знаете некоторые ее свойства.<br>Точно так же можно считать, что в предыдущем параграфе вы получили некоторые представления еще о трех функциях: [[Image:Alg42.jpg|240px|Функции]] Все эти [[Основные понятия|функции]] называют тригонометрическими функциями числового аргумента t. |
| | | | |
| - | '''Р е ш е н и е.''' а) Имеем:
| + | Есть целый ряд соотношений, связывающих значения различных тригонометрических функций, неметрические которые из этих соотношений вы уже знаете: |
| | | | |
| - | [[Image:alg46.jpg]]<br>Мы получили еще две важные формулы: | + | [[Image:Alg43.jpg|240px|Формулы]] |
| | | | |
| - | [[Image:alg47.jpg]]<br>Все указанные формулы используются в тех случаях, когда, зная значение какой-либо тригонометрической функции, требуется вычислить значения остальных тригонометрических функций.<br>'''Пример 2.''' Известно, что [[Image:alg48.jpg]] Вычислить соответствующие значения [[Image:alg49.jpg]]
| + | Из двух последних формул легко получить соотношение, связывающее tg t и ctg t |
| | | | |
| - | Р е ш е н и е. Из соотношения
| + | [[Image:Alg44.jpg|240px|Формулы]]<br>'''Пример 1.''' |
| | | | |
| - | [[Image:alg410.jpg]]<br>Из уравнения соз2 2 = — находим, что соз 2 = - или сое 2 = - ~. По<br>условию, аргумент 2 принадлежит первой четверти числовой окружности, а в ней соз 2 > 0. Значит, из двух указанных выше возможно-<br>4<br>стеи выбираем первую: сое I = ^ .<br>Зная значения зш 2 и сое 2, нетрудно вычислить соответствующие значения 2 и с*,^ 2:<br>зш I 3 4 3 . 1 4<br>^ I =-----= с!^ 2 =-= -.<br>К соз 2 5 5 4' 1В * 3<br>4 3 4 Ответ: соз 1= - ; - ~ ; 2 = - .<br>5 4 о<br>5 71<br>Пример 3. Известно, что ^ = ~ ^ > 2 Найти значе-<br>ния 3111 2, соз 2, сЬ& 2.<br>Решение. Воспользуемся соотношением<br>1 + 1*4= 1<br>соз'11<br>По условию, 2 = - — , значит,<br>_ Г 5 V 169 ' , 144<br>соз2 2 = 1 + 12 ] = Ш>асов*= ШГ<br>Из последнего уравнения находим, что<br>12 12<br>соз 2 = — или соз 2 = - —.<br>По условию, аргумент 2 принадлежит второй четверти числовой окружности, а в ней соз 2 < 0. Значит, из двух указанных выше возможностей выбираем вторую:<br>12<br>соз2 = --.<br>176<br>5.21.Ц<br>ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ<br>Зная значения * и соа I, нетрудно вычислить соответствующие значения зт I и с1;§ V.<br>Тз;<br>81114<br>=-, значит, зт 1 = соа I =<br>соз I<br>' 5 ' ' 12'<br>Г 12, Г<br><br>1<br>Ьё* 5<br>12<br>У<br>12 5 12<br>О т в е т: соз I = -— ; зт<=7^; •<br>1о 1о 5 | + | Упростить [[Повторення таблиць додавання і віднімання. Складання виразів за текстовим формулюванням|выражение]]: |
| | | | |
| - | А.Г. Мордкович Алгебра 9 класс | + | [[Image:Alg45.jpg|180px|Пример]] |
| | + | |
| | + | '''Решение.''' |
| | + | |
| | + | а) Имеем: |
| | + | |
| | + | [[Image:Alg46.jpg|420px|Р е ш е н и е]] |
| | + | |
| | + | Мы получили еще две важные формулы: |
| | + | |
| | + | [[Image:Alg47.jpg|240px|Формулы]] |
| | + | |
| | + | Все указанные формулы используются в тех случаях, когда, зная значение какой-либо тригонометрической функции, требуется вычислить значения остальных тригонометрических функций. |
| | + | |
| | + | <br>'''Пример 2.''' |
| | + | |
| | + | Известно, что [[Image:Alg48.jpg|140px|Пример]] Вычислить соответствующие значения [[Image:Alg49.jpg|120px|Пример]] |
| | + | |
| | + | '''Решение'''. |
| | + | |
| | + | Из соотношения |
| | + | |
| | + | [[Image:Alg410.jpg|320px|Решение]]<br>Из уравнения [[Image:Alg411.jpg|Решение]] находим, что [[Image:Alg412.jpg|180px|Решение]] По условию, аргумент t принадлежит первой четверти [[2. Числовая окружность|числовой окружности]], а в ней соs t > 0. Значит, из двух указанных выше возможностеи выбираем первую: [[Image:Alg413.jpg|Решение]]<br>Зная значения sin t и соs t, нетрудно вычислить соответствующие значения tg t и ctg t: |
| | + | |
| | + | [[Image:Alg414.jpg|320px|Решение]]<br>'''Пример 3. ''' |
| | + | |
| | + | Известно, что [[Image:Alg415.jpg|180px|Пример]] Найти значения sin t, соs t, ctg t.<br>'''Решение.''' |
| | + | |
| | + | Воспользуемся соотношением |
| | + | |
| | + | [[Image:Alg416.jpg|420px|Решение]] |
| | + | |
| | + | По условию, аргумент t принадлежит второй четверти числовой окружности, а в ней соs t < 0. Значит, из двух указанных выше возможностей выбираем вторую: |
| | + | |
| | + | [[Image:Alg417.jpg|Решение]]<br>Зная значения tg t и соs t, нетрудно вычислить соответствующие значения sin t и сtg t. |
| | + | |
| | + | [[Image:Alg418.jpg|420px|Решение]]<br><br><br> |
| | + | |
| | + | ''А.Г. Мордкович [http://xvatit.com/vuzi/ Алгебра] 9 класс'' |
| | | | |
| | <br> | | <br> |
| Строка 28: |
Строка 68: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 19:01, 10 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента
Какое бы действительное число t ни взять, ему можно поставить в соответствие однозначно определенное число t. Правда, правило соответствия довольно сложное, оно, как мы видели выше, заключается в следующем. Чтобы, по числу t найти значение sin t, нужно:
1) расположить числовую окружность в координатной плоскости так, чтобы центр окружности совпал с началом координат, а начальная точка А окружности попала в точку (1; 0);
2) на окружности найти точку, соответствующую числу 2;
3) найти ординату этой точки. Эта ордината и есть sin t.
Фактически речь идет о функции u = sin t, где 2 — любое действительное число. Вы умеете вычислять некоторые значения этой функции (например,  , знаете некоторые ее свойства. , знаете некоторые ее свойства.
Точно так же можно считать, что в предыдущем параграфе вы получили некоторые представления еще о трех функциях: 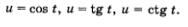 Все эти функции называют тригонометрическими функциями числового аргумента t. Все эти функции называют тригонометрическими функциями числового аргумента t.
Есть целый ряд соотношений, связывающих значения различных тригонометрических функций, неметрические которые из этих соотношений вы уже знаете:
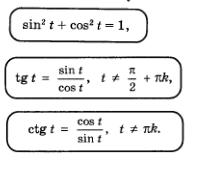
Из двух последних формул легко получить соотношение, связывающее tg t и ctg t
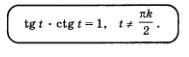
Пример 1.
Упростить выражение:
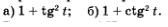
Решение.
а) Имеем:
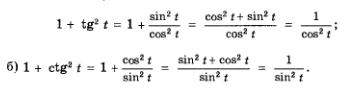
Мы получили еще две важные формулы:
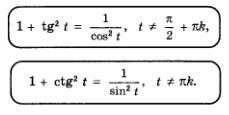
Все указанные формулы используются в тех случаях, когда, зная значение какой-либо тригонометрической функции, требуется вычислить значения остальных тригонометрических функций.
Пример 2.
Известно, что 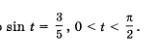 Вычислить соответствующие значения Вычислить соответствующие значения 
Решение.
Из соотношения
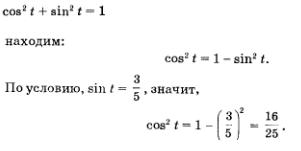
Из уравнения 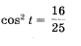 находим, что находим, что 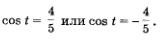 По условию, аргумент t принадлежит первой четверти числовой окружности, а в ней соs t > 0. Значит, из двух указанных выше возможностеи выбираем первую: По условию, аргумент t принадлежит первой четверти числовой окружности, а в ней соs t > 0. Значит, из двух указанных выше возможностеи выбираем первую: 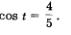
Зная значения sin t и соs t, нетрудно вычислить соответствующие значения tg t и ctg t:
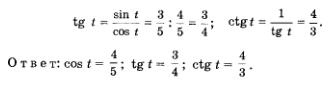
Пример 3.
Известно, что 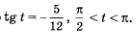 Найти значения sin t, соs t, ctg t. Найти значения sin t, соs t, ctg t.
Решение.
Воспользуемся соотношением

По условию, аргумент t принадлежит второй четверти числовой окружности, а в ней соs t < 0. Значит, из двух указанных выше возможностей выбираем вторую:
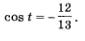
Зная значения tg t и соs t, нетрудно вычислить соответствующие значения sin t и сtg t.
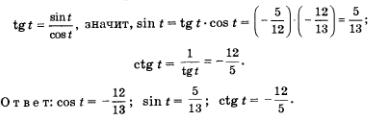
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|