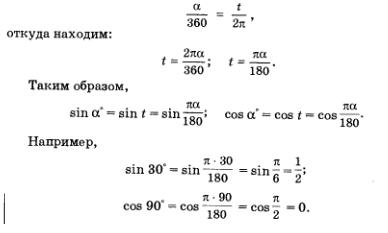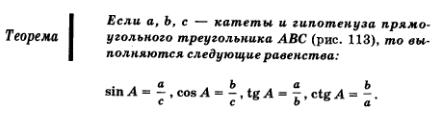|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Тригонометрические функции углового аргумента<metakeywords>Тригонометрические функции углового аргумента</metakeywords>''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Тригонометрические функции углового аргумента<metakeywords>Тригонометрические функции углового аргумента? косинус, синуса, окружностью, сантиметры, аргументом, прямоугольный треугольник</metakeywords>''' |
| | + | <br> |
| | | | |
| - | ТРИГОНОМЕТРИЧЕСКАЯ ФУНКЦИЯ УГЛОВОГО АРГУМЕНТА<br>Термины «синус», «косинус», «тангенс» и «котангенс» на самом деле были вам знакомы, правда, использовали вы их до сих пор в несколько иной интерпретации: в геометрии и в физике рассматривали синус, косинус, тангенс и котангенс у г л а (а не числа, как это было в предыдущих параграфах).<br>Из геометрии известно, что синус (косинус) острого угла — это отношение катета прямоугольного треугольника к его гипотенузе, а тангенс (котангенс) угла — это отношение катетов прямоугольного треугольника. Иной подход к понятиям синуса, косинуса, тангенса и котангенса развивали мы в предыдущих параграфах. На самом деле эти подходы взаимосвязаны, в чем мы сейчас убедимся.<br>Возьмем угол с градусной мерой <х° и расположим его в модели «числовая окружность в прямоугольной системе координат» так, как показано на рис. 112: вершину угла совместим с центром окружности (с началом системы координат), а одну сторону угла совместим с положительным лучом оси абсцисс. Точку пересечения второй стороны угла с окружностью обозначим буквой М. Ординату точки М естественно считать синусом угла а°, а абсциссу этой точки — косинусом угла а°.
| + | '''Тригонометрические функции углового аргумента'''<br> |
| | | | |
| - | [[Image:alg51.jpg]]<br>Для отыскания синуса или косинуса угла а° совсем не обязательно каждый раз делать указанные весьма сложные построения. Достаточно заметить, что дуга АМ составляет такую же<br>часть длины числовой окружности, какую угол а составляет от угла 360°. Если длину дуги АМ обозначить буквой то получим: | + | <br>Термины «синус», «[[Косинус угла. Полные уроки|косинус]]», «тангенс» и «котангенс» на самом деле были вам знакомы, правда, использовали вы их до сих пор в несколько иной интерпретации: в геометрии и в физике рассматривали синус, косинус, тангенс и котангенс угла (а не числа, как это было в предыдущих параграфах).<br> |
| | | | |
| - | [[Image:alg52.jpg]]<br>Считают, что 30° — это градусная мера угла, а | + | Из геометрии известно, что синус (косинус) острого угла — это отношение катета прямоугольного треугольника к его гипотенузе, а тангенс (котангенс) угла — это отношение катетов прямоугольного треугольника. Иной подход к понятиям [[4. Синус и косинус|синуса]], косинуса, тангенса и котангенса развивали мы в предыдущих параграфах. На самом деле эти подходы взаимосвязаны, в чем мы сейчас убедимся.<br> |
| | | | |
| - | [[Image:alg53.jpg]]<br>Ради краткости условились обозначение «рад» опускать, т.е. вполне допустимой является следующая запись:
| + | Возьмем угол с градусной мерой <х° и расположим его в модели «числовая окружность в прямоугольной системе координат» так, как показано на рис. 112: вершину угла совместим с центром окружности (с началом системы координат), а одну сторону угла совместим с положительным лучом оси абсцисс. Точку пересечения второй стороны угла с [[Окружность и круг|окружностью]] обозначим буквой М. Ординату точки М естественно считать синусом угла а°, а абсциссу этой точки — косинусом угла а°. |
| | | | |
| - | [[Image:alg54.jpg]]<br>Так что же такое 1 радиан? Вы знаете, что есть различные меры длин отрезков: сантиметры, метры, ярды и т.д. Есть и различные меры для обозначения величин углов. Мы рассматриваем центральные углы единичной окружности. Угол в 1° — это центральный угол, опирающийся на дугу, составляющую [[Image:alg55.jpg]] часть окружности. Угол в 1 радиан — 360 это центральный угол, опирающийся на дугу длиной 1, т.е. на дугу, длина которой равна радиусу 180° окружности. Из формулы [[Image:alg56.jpg]] получаем, 1 рад : что 1 рад = 57,3°.<br>Рассматривая функцию u = sin t (или любую другую тригонометрическую функцию), мы можем считать независимую переменную t числовым аргументом, как это было в предыдущих параграфах, но можем считать эту переменную и мерой угла, т.е. угловым аргументом. Поэтому, говоря о тригонометрической функции, в определенном смысле безразлично считать ее функцией числового или углового аргумента.<br>Завершая этот параграф, убедимся в том, что определения синуса, косинуса, тангенса и котангенса, которые вы изучали в геометрии, представляют собой частные случаи тех определений, что были предложены в этой главе. | + | [[Image:Alg51.jpg|240px|Числовая окружность]]<br> |
| | | | |
| - | [[Image:alg57.jpg]]<br>Доказательство. Совместим прямоугольный треугольник АВС с числовой окружностью так, как показано на рис. 114: вершину А поместим в центр окружности, катет АС «пустим» по положительному направлению оси абсцисс. Точку пересечения гипотенузы АВ с окружностью обозначим буквой М. Опустим из точки М перпендикуляр МР на прямую АС. Заметим, что АР и МР — абсцисса и ордината точки М, т.е. АР = соз А, МР = зш А. Учтем также, что АМ = 1 (радиус числовой окружности равен 1) и что АВ = с, АС = Ь, ВС = а.<br>Так как треугольники АМР и АВС подобны, то
| + | Для отыскания синуса или косинуса угла а° совсем не обязательно каждый раз делать указанные весьма сложные построения. Достаточно заметить, что дуга АМ составляет такую же часть длины числовой окружности, какую угол а составляет от угла 360°. Если длину дуги АМ обозначить буквой то получим: |
| | | | |
| - | [[Image:alg58.jpg]]<br>Теорема полностью доказана. | + | [[Image:Alg52.jpg|420px|Решение]]<br>Считают, что 30° — это градусная мера угла, а |
| | | | |
| | + | [[Image:Alg53.jpg|420px|Решение]]<br>Ради краткости условились обозначение «рад» опускать, т.е. вполне допустимой является следующая запись: |
| | | | |
| | + | [[Image:Alg54.jpg|240px|Решение]]<br>Так что же такое 1 радиан? Вы знаете, что есть различные меры длин отрезков: [[Вимірювання довжини відрізків у сантиметрах та дециметрах і сантиметрах|сантиметры]], метры, ярды и т.д. Есть и различные меры для обозначения величин углов. Мы рассматриваем центральные углы единичной окружности. Угол в 1° — это центральный угол, опирающийся на дугу, составляющую часть окружности. Угол в 1 радиан — 360 это центральный угол, опирающийся на дугу длиной 1, т.е. на дугу, длина которой равна радиусу 180° окружности. Из формулы получаем, 1 рад : что 1 рад = 57,3°. |
| | | | |
| - | А.Г. Мордкович Алгебра 9 класс | + | Рассматривая функцию u = sin t (или любую другую тригонометрическую функцию), мы можем считать независимую переменную t числовым аргументом, как это было в предыдущих параграфах, но можем считать эту переменную и мерой угла, т.е. угловым [[Тригонометрические функции числового аргумента|аргументом]]. Поэтому, говоря о тригонометрической функции, в определенном смысле безразлично считать ее функцией числового или углового аргумента. |
| | + | |
| | + | Завершая этот параграф, убедимся в том, что определения синуса, косинуса, тангенса и котангенса, которые вы изучали в геометрии, представляют собой частные случаи тех определений, что были предложены в этой главе. |
| | + | |
| | + | [[Image:Alg57.jpg|480px|Теорема]]<br>Доказательство. Совместим [[Співвідношення між сторонами і кутами прямокутного трикутника|прямоугольный треугольник]] АВС с числовой окружностью так, как показано на рис. 114: вершину А поместим в центр окружности, катет АС «пустим» по положительному направлению оси абсцисс. Точку пересечения гипотенузы АВ с окружностью обозначим буквой М. Опустим из точки М перпендикуляр МР на прямую АС. Заметим, что АР и МР — абсцисса и ордината точки М, т.е. АР = соs А, МР = sin А. Учтем также, что АМ = 1 (радиус числовой окружности равен 1) и что АВ = с, АС = b, ВС = а. |
| | + | |
| | + | Так как треугольники АМР и АВС подобны, то |
| | + | |
| | + | [[Image:Alg58.jpg|480px|Теорема]]<br>Теорема полностью доказана.<br> |
| | + | |
| | + | |
| | + | |
| | + | ''А.Г. Мордкович [http://xvatit.com/vuzi/ Алгебра] 9 класс'' |
| | | | |
| | <br> | | <br> |
| Строка 24: |
Строка 39: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 19:16, 10 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Тригонометрические функции углового аргумента
Тригонометрические функции углового аргумента
Термины «синус», «косинус», «тангенс» и «котангенс» на самом деле были вам знакомы, правда, использовали вы их до сих пор в несколько иной интерпретации: в геометрии и в физике рассматривали синус, косинус, тангенс и котангенс угла (а не числа, как это было в предыдущих параграфах).
Из геометрии известно, что синус (косинус) острого угла — это отношение катета прямоугольного треугольника к его гипотенузе, а тангенс (котангенс) угла — это отношение катетов прямоугольного треугольника. Иной подход к понятиям синуса, косинуса, тангенса и котангенса развивали мы в предыдущих параграфах. На самом деле эти подходы взаимосвязаны, в чем мы сейчас убедимся.
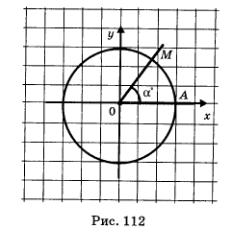
Возьмем угол с градусной мерой <х° и расположим его в модели «числовая окружность в прямоугольной системе координат» так, как показано на рис. 112: вершину угла совместим с центром окружности (с началом системы координат), а одну сторону угла совместим с положительным лучом оси абсцисс. Точку пересечения второй стороны угла с окружностью обозначим буквой М. Ординату точки М естественно считать синусом угла а°, а абсциссу этой точки — косинусом угла а°.
Для отыскания синуса или косинуса угла а° совсем не обязательно каждый раз делать указанные весьма сложные построения. Достаточно заметить, что дуга АМ составляет такую же часть длины числовой окружности, какую угол а составляет от угла 360°. Если длину дуги АМ обозначить буквой то получим:
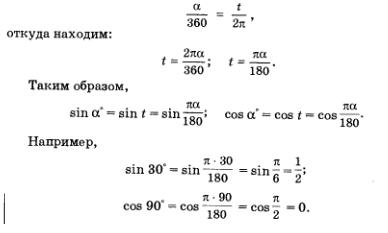
Считают, что 30° — это градусная мера угла, а

Ради краткости условились обозначение «рад» опускать, т.е. вполне допустимой является следующая запись:
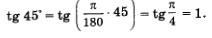
Так что же такое 1 радиан? Вы знаете, что есть различные меры длин отрезков: сантиметры, метры, ярды и т.д. Есть и различные меры для обозначения величин углов. Мы рассматриваем центральные углы единичной окружности. Угол в 1° — это центральный угол, опирающийся на дугу, составляющую часть окружности. Угол в 1 радиан — 360 это центральный угол, опирающийся на дугу длиной 1, т.е. на дугу, длина которой равна радиусу 180° окружности. Из формулы получаем, 1 рад : что 1 рад = 57,3°.
Рассматривая функцию u = sin t (или любую другую тригонометрическую функцию), мы можем считать независимую переменную t числовым аргументом, как это было в предыдущих параграфах, но можем считать эту переменную и мерой угла, т.е. угловым аргументом. Поэтому, говоря о тригонометрической функции, в определенном смысле безразлично считать ее функцией числового или углового аргумента.
Завершая этот параграф, убедимся в том, что определения синуса, косинуса, тангенса и котангенса, которые вы изучали в геометрии, представляют собой частные случаи тех определений, что были предложены в этой главе.
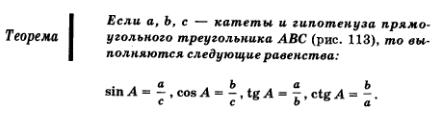
Доказательство. Совместим прямоугольный треугольник АВС с числовой окружностью так, как показано на рис. 114: вершину А поместим в центр окружности, катет АС «пустим» по положительному направлению оси абсцисс. Точку пересечения гипотенузы АВ с окружностью обозначим буквой М. Опустим из точки М перпендикуляр МР на прямую АС. Заметим, что АР и МР — абсцисса и ордината точки М, т.е. АР = соs А, МР = sin А. Учтем также, что АМ = 1 (радиус числовой окружности равен 1) и что АВ = с, АС = b, ВС = а.
Так как треугольники АМР и АВС подобны, то
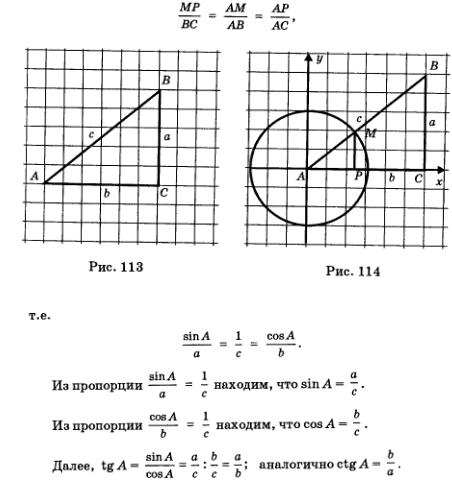
Теорема полностью доказана.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|