|
|
| (1 промежуточная версия не показана) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Признак подобия тельников по двум углам</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Признак подобия тельников по двум углам, треугольника, преобразованию подобия, подобны, секущей</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Признак подобия тельников по двум углам''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Признак подобия тельников по двум углам''' |
| | | | |
| - | <br> | + | <br> '''Признак подобия тельников по двум углам'''<br> |
| | | | |
| - | '''ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПО ДВУМ УГЛАМ'''<br>
| + | <br>'''Теорема 11.2.''' Если два угла одного [[Презентація уроку на тему «Трикутник і його елементи»|треугольника]] равны двум углам другого треугольника, то такие треугольники подобны. |
| | | | |
| - | <br>Теорема 11.2.'''''Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны'''''.
| + | '''Доказательство'''. Пусть у треугольников ABC и A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> [[Image:20-06-61.jpg]]A=[[Image:20-06-61.jpg]]A<sub>1</sub>, [[Image:20-06-61.jpg]]B=[[Image:20-06-61.jpg]]B<sub>1</sub>. Докажем, что [[Image:21-06-11.jpg]]АВС [[Image:24-06-6.jpg]][[Image:21-06-11.jpg]]A<sub>1</sub>B<sub>1</sub>C<sub>1</sub>.<br> |
| | | | |
| - | Доказательство. Пусть у треугольников ABC и A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> [[Image:20-06-61.jpg]]A=[[Image:20-06-61.jpg]]A<sub>1</sub>, [[Image:20-06-61.jpg]]B=[[Image:20-06-61.jpg]]B<sub>1</sub>. Докажем, что [[Image:21-06-11.jpg]]АВС [[Image:24-06-6.jpg]][[Image:21-06-11.jpg]]A<sub>1</sub>B<sub>1</sub>C<sub>1</sub>.<br>
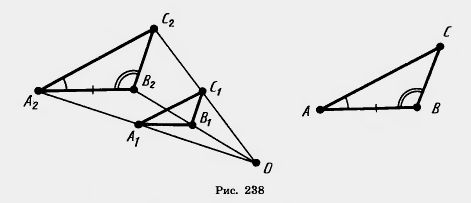
| + | Пусть [[Image:24-06-9.jpg|Формула]] . Подвергнем треугольник A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> [[Преобразование подобия|преобразованию подобия]] с коэффициентом подобия k, например гомотетии (рис. 238). При этом получим некоторый треугольник A<sub>2</sub>B<sub>2</sub>C<sub>2</sub>, равный треугольнику ABC. Действительно, так как преобразование подобия сохраняет углы, то [[Image:20-06-61.jpg]]A<sub>2</sub>=[[Image:20-06-61.jpg]]A<sub>1</sub>, [[Image:20-06-61.jpg]]B<sub>2</sub>=[[Image:20-06-61.jpg]]B<sub>1</sub>.. значит, у треугольников ABC и A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> [[Image:20-06-61.jpg]]A=[[Image:20-06-61.jpg]]A<sub>2</sub>, [[Image:20-06-61.jpg]]B=[[Image:20-06-61.jpg]]B<sub>2</sub>. Далее, A<sub>2</sub>B<sub>2</sub> — kA<sub>1</sub>B<sub>1</sub>=AB. Следовательно, треугольники ABC и A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> равны по второму признаку (по стороне и прилежащим к ней углам).<br> <br>[[Image:24-06-10.jpg|480px|Признак подобия тельников по двум углам]] |
| | | | |
| - | Пусть [[Image:24-06-9.jpg]] . Подвергнем треугольник A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> преобразованию подобия с коэффициентом подобия k, например гомотетии (рис. 238). При этом получим некоторый треугольник A<sub>2</sub>B<sub>2</sub>C<sub>2</sub>, равный треугольнику ABC. Действительно, так как преобразование подобия сохраняет углы, то [[Image:20-06-61.jpg]]A<sub>2</sub>=[[Image:20-06-61.jpg]]A<sub>1</sub>, [[Image:20-06-61.jpg]]B<sub>2</sub>=[[Image:20-06-61.jpg]]B<sub>1</sub>.. значит, у треугольников ABC и A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> [[Image:20-06-61.jpg]]A=[[Image:20-06-61.jpg]]A<sub>2</sub>, [[Image:20-06-61.jpg]]B=[[Image:20-06-61.jpg]]B<sub>2</sub>. Далее, A<sub>2</sub>B<sub>2</sub> — kA<sub>1</sub>B<sub>1</sub>=AB. Следовательно, треугольники ABC и A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> равны по второму признаку (по стороне и прилежащим к ней углам).<br> <br>[[Image:24-06-10.jpg]]
| + | <br>Так как треугольники A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> и A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> гомотетичны и, значит, подобны, а треугольники A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> и АBС равны и поэтому тоже [[Презентація уроку: Перетворення подібності. Гомотетія, властивості подібних фігур.|подобны]], то треугольники A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> и АBС подобны. Теорема доказана.<br> <br>[[Image:24-06-11.jpg|480px|Признак подобия тельников по двум углам]] |
| | | | |
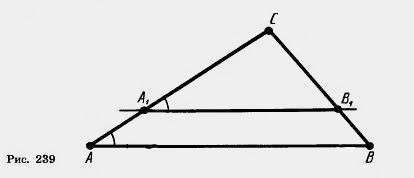
| - | <br>Так как треугольники A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> и A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> гомотетичны и, значит, подобны, а треугольники A<sub>2</sub>B<sub>2</sub>C<sub>2</sub> и АBС равны и поэтому тоже подобны, то треугольники A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> и АBС подобны. Теорема доказана.<br> <br>[[Image:24-06-11.jpg]] | + | <br>'''Задача (15).''' Прямая, параллельная стороне АB треугольника АBС, пересекает его сторону АС в точке А<sub>1</sub>, а сторону БС в точке B<sub>1</sub>. Докажите, что[[Image:21-06-11.jpg]]ABC [[Image:24-06-6.jpg]] [[Image:21-06-11.jpg]]A<sub>1</sub>B<sub>1</sub>C. |
| | | | |
| - | <br>Задача (15). Прямая, параллельная стороне АB треугольника АBС, пересекает его сторону АС в точке А<sub>1</sub>, а сторону БС в точке B<sub>1</sub>. Докажите, что
| + | '''Решение (рис. 239).''' У треугольников АBС и A<sub>1</sub>B<sub>1</sub>C угол при вершине С общий, а углы CA<sub>1</sub>B<sub>1</sub> и CAB равны как соответствующие углы параллельных АВ и A<sub>1</sub>B<sub>1</sub> с [[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|секущей]] АС. Следовательно, [[Image:21-06-11.jpg]]ABC [[Image:24-06-6.jpg]] [[Image:21-06-11.jpg]]A<sub>1</sub>B<sub>1</sub>C.по двум углам. <br> |
| | | | |
| - | [[Image:21-06-11.jpg]]ABC [[Image:24-06-6.jpg]] [[Image:21-06-11.jpg]]A<sub>1</sub>B<sub>1</sub>C.
| + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Решение (рис. 239). У треугольников АBС и A<sub>1</sub>B<sub>1</sub>C угол при вершине С общий, а углы CA<sub>1</sub>B<sub>1</sub> и CAB равны как соответствующие углы параллельных АВ и A<sub>1</sub>B<sub>1</sub> с секущей АС. Следовательно, <br>
| + | <br> |
| - | | + | |
| - | [[Image:21-06-11.jpg]]ABC [[Image:24-06-6.jpg]] [[Image:21-06-11.jpg]]A<sub>1</sub>B<sub>1</sub>C.по двум углам. <br>
| + | |
| - | | + | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| + | |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> |
| Строка 30: |
Строка 26: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.