|
|
| (1 промежуточная версия не показана) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Алгебра, урок, на Тему, Соотношение между углами треугольника, противолежащими сторонами</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Соотношение между углами треугольника, противолежащими сторонами, угол, треугольника, треугольник равнобедренный</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Соотношение между углами треугольника и противолежащими сторонами''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Соотношение между углами треугольника и противолежащими сторонами''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' СООТНОШЕНИЕ МЕЖДУ УГЛАМИ ТРЕУГОЛЬНИКА И ПРОТИВОЛЕЖАЩИМИ СТОРОНАМИ''' | + | '''Соотношение между углами треугольника и противолежащими сторонами''' |
| | | | |
| - | <br>В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол. | + | <br>В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший [[Угол. Прямой и развернутый угол. Чертежный треугольник|угол]]. |
| | | | |
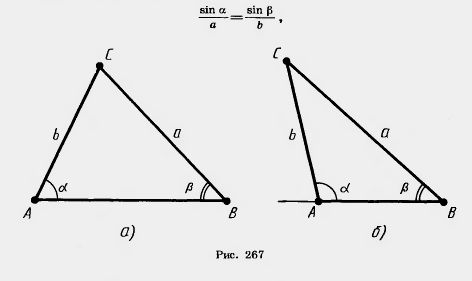
| - | Пусть а и b — две стороны треугольника и [[Image:24-06-52.jpg]], [[Image:24-06-53.jpg]] — противолежащие им углы. Докажем, что если [[Image:24-06-52.jpg]] > [[Image:24-06-53.jpg]], то а > b. И обратно: если а>b, то [[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]].<br>Если углы [[Image:24-06-52.jpg]] и [[Image:24-06-53.jpg]] острые (рис. 267, с), то при [[Image:24-06-52.jpg]] > [[Image:24-06-53.jpg]] будет sin [[Image:24-06-52.jpg]]>sin [[Image:24-06-53.jpg]]. А так как<br>sin [[Image:24-06-52.jpg]] sin [[Image:24-06-53.jpg]]<br> | + | Пусть а и b — две стороны треугольника и [[Image:24-06-52.jpg]], [[Image:24-06-53.jpg]] — противолежащие им углы. Докажем, что если [[Image:24-06-52.jpg]] > [[Image:24-06-53.jpg]], то а > b. И обратно: если а>b, то [[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]]. |
| | | | |
| - | [[Image:24-06-51.jpg]]<br>Рис. 267<br><br>то а > b. Если угол [[Image:24-06-52.jpg]] тупой (оба угла не могут быть тупыми), то угол 180° — [[Image:24-06-52.jpg]] острый (рис. 267, б). Причем угол 180° — [[Image:24-06-52.jpg]] больше угла [[Image:24-06-53.jpg]] как внешний угол треугольника, не смежный с углом [[Image:24-06-53.jpg]]. Поэтому sin [[Image:24-06-52.jpg]] = sin (180° —а) > sin [[Image:24-06-53.jpg]]. И мы снова заключаем, что а>b. | + | Если углы [[Image:24-06-52.jpg]] и [[Image:24-06-53.jpg]] острые (рис. 267, с), то при [[Image:24-06-52.jpg]] > [[Image:24-06-53.jpg]] будет sin [[Image:24-06-52.jpg]]>sin [[Image:24-06-53.jpg]]. А так как sin [[Image:24-06-52.jpg]] sin [[Image:24-06-53.jpg]] то а > b. <br> |
| | | | |
| - | Докажем обратное утверждение. Пусть а>b. Надо доказать, что [[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]]. Допустим, что [[Image:24-06-52.jpg]][[Image:24-06-54.jpg]][[Image:24-06-53.jpg]]. Если [[Image:24-06-52.jpg]] = [[Image:24-06-53.jpg]], то треугольник равнобедренный и а = b. Если [[Image:24-06-52.jpg]]<[[Image:24-06-53.jpg]], то по доказанному a<b. В обоих случаях получается противоречие, так как по предположению а>Ь, значит,[[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]], что и требовалось доказать.
| + | [[Image:24-06-51.jpg|480px|Соотношение между углами треугольника и противолежащими сторонами]]<br>''Рис. 267''<br><br>Если угол [[Image:24-06-52.jpg]] тупой (оба угла не могут быть тупыми), то угол 180° — [[Image:24-06-52.jpg]] острый (рис. 267, б). Причем угол 180° — [[Image:24-06-52.jpg]] больше угла [[Image:24-06-53.jpg]] как внешний угол [[Задачі до теми Лічба в межах 20. Розв’язування задач на віднімання. Розпізнавання трикутників|треугольника]], не смежный с углом [[Image:24-06-53.jpg]]. Поэтому sin [[Image:24-06-52.jpg]] = sin (180° —а) > sin [[Image:24-06-53.jpg]]. И мы снова заключаем, что а>b. |
| | | | |
| - | Задача (17). Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая. | + | Докажем обратное утверждение. Пусть а>b. Надо доказать, что [[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]]. Допустим, что [[Image:24-06-52.jpg]][[Image:24-06-54.jpg]][[Image:24-06-53.jpg]]. Если [[Image:24-06-52.jpg]] = [[Image:24-06-53.jpg]], то [[Равнобедренный треугольник. Полные уроки|треугольник равнобедренный]] и а = b. Если [[Image:24-06-52.jpg]]<[[Image:24-06-53.jpg]], то по доказанному a<b. В обоих случаях получается противоречие, так как по предположению а>Ь, значит,[[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]], что и требовалось доказать. |
| | + | |
| | + | Задача (17). Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая. |
| | | | |
| | Решение. В треугольнике может быть только один тупой угол. Поэтому он больше любого из остальных углов. А значит, противолежащая ему сторона больше любой из двух других сторон треугольника. <br> | | Решение. В треугольнике может быть только один тупой угол. Поэтому он больше любого из остальных углов. А значит, противолежащая ему сторона больше любой из двух других сторон треугольника. <br> |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | + | |
| | + | |
| | | | |
| | <sub>Планы конспектов уроков по математике 9 класса [[Математика|скачать]], учебники и книги бесплатно, разработки уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Планы конспектов уроков по математике 9 класса [[Математика|скачать]], учебники и книги бесплатно, разработки уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 26: |
Строка 30: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Задача (17). Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая.
Решение. В треугольнике может быть только один тупой угол. Поэтому он больше любого из остальных углов. А значит, противолежащая ему сторона больше любой из двух других сторон треугольника.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.