|
|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Выпуклые многоугольники''' <br> | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Выпуклые многоугольники''' <br> |
| | | | |
| - | | + | <br> |
| | | | |
| | '''Выпуклые многоугольники'''<br> | | '''Выпуклые многоугольники'''<br> |
| | | | |
| - | <br>[[Урок 6. Длина ломаной. Периметр|Ломаная]] | + | <br>[[Урок 6. Длина ломаной. Периметр|Ломанаяназывается]] замкнутой, если у нее концы совпадают. Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой (рис. 276). Вершины ломаной называются вершинами многоугольника, а звенья ломаной — сторонами многоугольника. |
| - | называется замкнутой, если у нее концы совпадают. Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой (рис. 276). Вершины ломаной называются вершинами многоугольника, а звенья ломаной — сторонами многоугольника.
| + | |
| | | | |
| | Отрезки, соединяющие не соседние вершины [[Площадь ортогональной проекции многоугольника|многоугольник]], называются диагоналями. Многоугольник с n вершинами, а значит, и с n сторонами называется n-угольником.<br> | | Отрезки, соединяющие не соседние вершины [[Площадь ортогональной проекции многоугольника|многоугольник]], называются диагоналями. Многоугольник с n вершинами, а значит, и с n сторонами называется n-угольником.<br> |
| Строка 28: |
Строка 27: |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | | + | <br> |
| | | | |
| | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> | | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> |
Текущая версия на 11:47, 11 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Выпуклые многоугольники
Выпуклые многоугольники
Ломанаяназывается замкнутой, если у нее концы совпадают. Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой (рис. 276). Вершины ломаной называются вершинами многоугольника, а звенья ломаной — сторонами многоугольника.
Отрезки, соединяющие не соседние вершины многоугольник, называются диагоналями. Многоугольник с n вершинами, а значит, и с n сторонами называется n-угольником.
Плоским многоугольником или многоугольной областью называется конечная часть плоскости, ограниченная многоугольником (рис. 277).
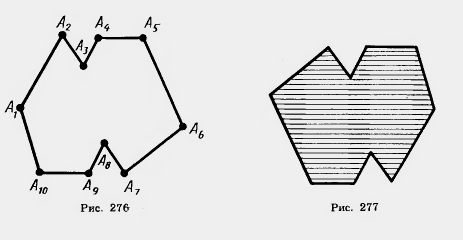
Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. При этом сама прямая считается принадлежащей полуплоскости. На рисунке 278, о изображен выпуклый многоугольник, а на рисунке 278, б — невыпуклый. Углом выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине.
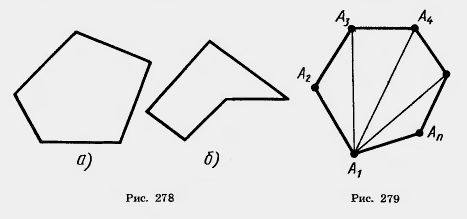
Теорема 13.2. Сумма углов выпуклого n-угольника равна 180°-(n-2).
Доказательство. В случае n = b теорема справедлива. Пусть A1A2 ... An —данный выпуклый многоугольник и n>b (рис. 279). Проведем n — b диагонали: А1А3, А1А4, ...A1An-1. Так как многоугольник выпуклый, то эти диагонали разбивают его на n —2 треугольника:  А1А2А3, А1А2А3,  А1А3А4, ... .... А1А3А4, ... ....  A1A1-nAn. A1A1-nAn.
Сумма углов многоугольника А1А2...Аn совпадает с суммой углов всех этих треугольников. Сумма углов каждого треугольника равна 180°, а число этих треугольников есть n — 2. Поэтому сумма углов выпуклого n-угольника А1А2...Аn равна 180°-(n —2). Теорема доказана.
Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине.
Задача (9). Чему равна сумма внешних углов выпуклого п-угольника, взятых по одному при каждой вершине?
Решение. Сумма внутреннего угла многоугольника и смежного с ним внешнего равна 180°. Поэтому сумма всех внутренних и внешних углов равна 180° • n. Но сумма всех внутренних углов равна 180°•(n — 2). Значит, сумма внешних углов, взятых по одному при каждой вершине, равна 180°• n-180°-(n-2)==360°.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












