KNOWLEDGE HYPERMARKET

Задачи-3(9-класс)
(Создана новая страница размером <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, ...)
 
(2 промежуточные версии не показаны)
Строка 1: Строка 1:
-
<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Алгебра, урок, на Тему, Задачи-3, (9-класс)</metakeywords>  
+
<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Задачи-3, окружности, ломаная, правильный многоугольник, перпендикулярная, квадрат, треугольник, периметра, угол</metakeywords>  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 9 класс|Математика 9 класс]]&gt;&gt;Математика:Задачи-3(9-класс)'''  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 9 класс|Математика 9 класс]]&gt;&gt;Математика:Задачи-3(9-класс)'''  
Строка 5: Строка 5:
<br>  
<br>  
-
'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ЗАДАЧИ'''<br><br><br>1. Даны две окружности с радиусами R<sub>1</sub> и R<sub>2</sub> и расстоянием между центрами d &gt; R<sub>1</sub> + R<sub>2.</sub> Чему равны наибольшее и наименьшее расстояния между точками X и У этих окружностей?
+
'''Задачи'''<br><br>1. Даны две [[Окружность, описанная около треугольника. Полные уроки|окружности]] с радиусами R<sub>1</sub> и R<sub>2</sub> и расстоянием между центрами d &gt; R<sub>1</sub> + R<sub>2.</sub> Чему равны наибольшее и наименьшее расстояния между точками X и У этих окружностей?  
-
2.&nbsp;&nbsp; &nbsp;Решите задачу 1 при условии, что d&lt;.R<sub>1</sub> - R2 (рис. 291).<br>
+
2. Решите задачу 1 при условии, что d&lt;.R<sub>1</sub> - R2 (рис. 291).<br>  
-
3.&nbsp;&nbsp; &nbsp;Докажите, что если вершины ломаной не лежат на одной прямой, то длина ломаной больше длины отрезка, соединяющего ее концы.<br>
+
3. Докажите, что если вершины ломаной не лежат на одной прямой, то длина ломаной больше длины отрезка, соединяющего ее концы.<br>  
-
4.&nbsp;&nbsp; &nbsp;Докажите, что у замкнутой ломаной расстояние между любыми двумя вершинами не больше половины длины ломаной.<br>
+
4. Докажите, что у замкнутой ломаной расстояние между любыми двумя вершинами не больше половины длины ломаной.<br>  
-
5.&nbsp;&nbsp; &nbsp;Докажите, что у замкнутой ломаной длина каждого звена не больше суммы длин остальных звеньев.<br>
+
5. Докажите, что у замкнутой ломаной длина каждого звена не больше суммы длин остальных звеньев.<br>  
-
6.&nbsp;&nbsp; &nbsp;Может ли замкнутая ломаная иметь звенья длиной 1 м, 2 м, 3 м, 4 м, 11 м? Объясните ответ.<br>
+
6. Может ли замкнутая [[Урок 6. Длина ломаной. Периметр|ломаная]] иметь звенья длиной 1 м, 2 м, 3 м, 4 м, 11 м? Объясните ответ.<br>  
-
7.&nbsp;&nbsp; &nbsp;Докажите, что если концы ломаной лежат по разные стороны от данной прямой, то она пересекает эту прямую (рис. 292).<br>
+
7. Докажите, что если концы ломаной лежат по разные стороны от данной прямой, то она пересекает эту прямую (рис. 292).<br>  
-
8. Сколько диагоналей у n-угольника?<br>
+
8. Сколько диагоналей у n-угольника?<br>  
-
9. Чему равна сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине?<br>
+
9. Чему равна сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине?<br>  
-
[[Image:29-06-9.jpg]]<br>&nbsp; &nbsp;<br>10.&nbsp;&nbsp;&nbsp; Углы выпуклого четырехугольника пропорциональны числам 1, 2, 3, 4. Найдите их.
+
[[Image:29-06-9.jpg|480px|Окружность. Ломаная]]<br>&nbsp; &nbsp;<br>10. Углы выпуклого четырехугольника пропорциональны числам 1, 2, 3, 4. Найдите их.  
-
11.&nbsp;&nbsp;&nbsp; Докажите, что у четырехугольника, описанного около окружности, суммы длин противолежащих сторон равны.<br>
+
11. Докажите, что у четырехугольника, описанного около окружности, суммы длин противолежащих сторон равны.<br>  
-
12. Сколько сторон имеет правильный многоугольник, каждый&nbsp; из&nbsp;&nbsp; внутренних&nbsp;&nbsp; углов&nbsp;&nbsp; которого&nbsp;&nbsp; равен:<br>
+
12. Сколько сторон имеет [[Правильные многоугольники|правильный многоугольник]], каждый&nbsp; из&nbsp;&nbsp; внутренних&nbsp;&nbsp; углов&nbsp;&nbsp; которого&nbsp;&nbsp; равен:<br>  
-
1) 135°; 2) 150°?<br>
+
1) 135°; 2) 150°?<br>  
-
13.&nbsp;&nbsp;&nbsp; Сколько сторон имеет правильный многоугольник, если каждый из внешних его углов равен:<br>
+
13. Сколько сторон имеет правильный многоугольник, если каждый из внешних его углов равен:<br>  
-
1) 36°; 2) 24°?<br>
+
1) 36°; 2) 24°?<br>  
-
14.&nbsp;&nbsp;&nbsp; Докажите, что взятые через одну вершины правильного 2n-угольника являются вершинами правильного n-угольника.<br>
+
14. Докажите, что взятые через одну вершины правильного 2n-угольника являются вершинами правильного n-угольника.<br>  
-
15.&nbsp;&nbsp;&nbsp; Докажите, что середины сторон правильного n-угольника являются вершинами другого правильного n-угольника.<br>
+
15. Докажите, что середины сторон правильного n-угольника являются вершинами другого правильного n-угольника.<br>  
-
16. Найдите выражения для стороны а<sub>n</sub> правильного n-угольника через радиус R описанной около него окружности и радиус r вписанной окружности. Вычислите а<sub>n</sub> при n = 3, 4, 6.<br>
+
16. Найдите выражения для стороны а<sub>n</sub> правильного n-угольника через радиус R описанной около него окружности и радиус r вписанной окружности. Вычислите а<sub>n</sub> при n = 3, 4, 6.<br>  
-
17.&nbsp;&nbsp;&nbsp; Хорда, перпендикулярная радиусу и проходящая через его середину, равна стороне правильного вписанного треугольника. Докажите.<br>
+
17. Хорда, [[Поділ відрізка навпіл. Побудова перпендикулярної прямої|перпендикулярная]] радиусу и проходящая через его середину, равна стороне правильного вписанного треугольника. Докажите.<br>  
-
18.&nbsp;&nbsp;&nbsp; У правильного треугольника радиус вписанной окружности в два раза меньше радиуса описанной окружности. Докажите.<br>
+
18. У правильного треугольника радиус вписанной окружности в два раза меньше радиуса описанной окружности. Докажите.<br>  
-
19.&nbsp;&nbsp;&nbsp; Сторона правильного вписанного в окружность треугольника равна а. Найдите сторону квадрата, вписанного в эту окружность.<br>
+
19. Сторона правильного вписанного в окружность треугольника равна а. Найдите сторону квадрата, вписанного в эту окружность.<br>  
-
20.&nbsp;&nbsp;&nbsp; В окружность, радиус которой 4 дм, вписан правильный треугольник, на стороне которого построен квадрат. Найдите радиус окружности, описанной около квадрата.<br>
+
20. В окружность, радиус которой 4 дм, вписан правильный треугольник, на стороне которого построен квадрат. Найдите радиус окружности, описанной около квадрата.<br>  
-
21.&nbsp;&nbsp;&nbsp; Конец валика диаметром 4 см опилен под квадрат. Каким может быть наибольший размер стороны квадрата?<br>
+
21. Конец валика диаметром 4 см опилен под [[Ромб i його властивості, квадрат i його властивості|квадрат]]. Каким может быть наибольший размер стороны квадрата?<br>  
-
22.&nbsp;&nbsp;&nbsp; Конец винта газовой задвижки имеет правильную трехгранную форму. Каким Может быть наибольший размер грани, если диаметр цилиндрической части винта 2 см?<br>
+
22. Конец винта газовой задвижки имеет правильную трехгранную форму. Каким Может быть наибольший размер грани, если диаметр цилиндрической части винта 2 см?<br>  
-
23.&nbsp;&nbsp;&nbsp; Докажите, что сторона правильного 8-угольника вычисляется по формуле [[Image:29-06-10.jpg]] где R — радиус описанной окружности.<br>24.&nbsp;&nbsp;&nbsp; Докажите, что сторона правильного 12-угольника вычисляется по формуле [[Image:29-06-11.jpg]] где R — радиус<br>описанной окружности.
+
23. Докажите, что сторона правильного 8-угольника вычисляется по формуле [[Image:29-06-10.jpg|120px|Формула]] где R — радиус описанной окружности.<br>24. Докажите, что сторона правильного 12-угольника вычисляется по формуле [[Image:29-06-11.jpg|120px|Формула]] где R — радиус описанной окружности.  
-
25*. Найдите стороны правильного пятиугольника и правильного 10-угольника, вписанных в окружность радиуса R.<br>
+
25*. Найдите стороны правильного пятиугольника и правильного 10-угольника, вписанных в окружность радиуса R.<br>  
-
26. Сторона правильного многоугольника равна а, а радиус описанной окружности R. Найдите радиус вписанной окружности.
+
26. Сторона правильного многоугольника равна а, а радиус описанной окружности R. Найдите радиус вписанной окружности.  
-
27.&nbsp;&nbsp;&nbsp; Сторона правильного многоугольника равна а, а радиус вписанной окружности r. Найдите радиус описанной окружности.
+
27. Сторона правильного многоугольника равна а, а радиус вписанной окружности r. Найдите радиус описанной окружности.  
-
28.&nbsp;&nbsp;&nbsp; Выразите сторону b правильного описанного многоугольника через радиус R окружности и сторону а правильного вписанного многоугольника с тем же числом сторон.
+
28. Выразите сторону b правильного описанного многоугольника через радиус R окружности и сторону а правильного вписанного многоугольника с тем же числом сторон.  
-
29.&nbsp;&nbsp;&nbsp; Выразите сторону а правильного вписанного многоугольника через радиус R окружности и сторону b правильного описанного многоугольника с тем же числом сторон.
+
29. Выразите сторону а правильного вписанного многоугольника через радиус R окружности и сторону b правильного описанного многоугольника с тем же числом сторон.  
-
30. Впишите в окружность правильный 12-угольник.
+
30. Впишите в окружность правильный 12-угольник.  
-
31. Опишите около окружности правильный треугольник, квадрат, правильный восьмиугольник.
+
31. Опишите около окружности правильный [[Треугольник. Полные уроки|треугольник]], квадрат, правильный восьмиугольник.  
-
32. Радиусы вписанной и описанной окружностей одного правильного n-угольника равны r<sub>1</sub> и R<sub>1</sub>, а радиус вписанной окружности другого правильного n-угольника равен r<sub>2</sub>. Чему равен радиус описанной окружности другого n-угольника?
+
32. Радиусы вписанной и описанной окружностей одного правильного n-угольника равны r<sub>1</sub> и R<sub>1</sub>, а радиус вписанной окружности другого правильного n-угольника равен r<sub>2</sub>. Чему равен радиус описанной окружности другого n-угольника?  
-
33. Периметры двух правильных n-угольников относятся как а: b. Как относятся радиусы их вписанных и описанных окружностей?
+
33. Периметры двух правильных n-угольников относятся как а: b. Как относятся радиусы их вписанных и описанных окружностей?  
-
34. Вычислите длину окружности, если радиус равен:
+
34. Вычислите длину окружности, если радиус равен:1) 10 м; 2) 15 м.
-
1) 10 м; 2) 15 м.
+
35. На сколько изменится длина окружности, если радиус изменится на 1 мм?
-
35.&nbsp;&nbsp;&nbsp; На сколько изменится длина окружности, если радиус изменится на 1 мм?
+
36. Найдите отношение [[Прямокутник, квадрат, їх периметри. Презентація уроку|периметра]]&nbsp;правильного вписанного 8-угольника к диаметру и сравните его с приближенным значением [[Image:24-06-93.jpg]].
-
36.&nbsp;&nbsp;&nbsp; Найдите отношение периметра правильного вписанного 8-угольника к диаметру и сравните его с приближенным значением [[Image:24-06-93.jpg]].
+
37. Решите задачу 36 для правильного 12-угольника.  
-
37.&nbsp;&nbsp;&nbsp; Решите задачу 36 для правильного 12-угольника.
+
38. Найдите радиус земного шара, исходя из того, что 1 м составляет одну 40-миллионную долю длины экватора.  
-
38.&nbsp;&nbsp;&nbsp; Найдите радиус земного шара, исходя из того, что 1 м составляет одну 40-миллионную долю длины экватора.
+
39. На сколько удлинился бы земной экватор, если бы радиус земного шара увеличился на 1 см?
-
39.&nbsp;&nbsp;&nbsp; На сколько удлинился бы земной экватор, если бы радиус земного шара увеличился на 1 см?
+
40. Внутри окружности радиуса R расположены п равных окружностей, которые касаются друг друга и данной окружности. Найдите радиус этих окружностей, если число их равно:1) 3; 2) 4; 3) 6 (рис. 293).
-
40.&nbsp;&nbsp;&nbsp; Внутри окружности радиуса R расположены п равных окружностей, которые касаются друг друга и данной окружности. Найдите радиус этих окружностей, если число их равно:
+
41. Решите предыдущую задачу, если окружности расположены вне данной окружности.  
-
1) 3; 2) 4; 3) 6 (рис. 293).
+
42. Шкив имеет в диаметре 1,4 м и делает 80 оборотов в минуту. Найдите скорость точки на окружности шкива.  
-
 
+
-
41.&nbsp;&nbsp;&nbsp; Решите предыдущую задачу, если окружности расположены вне данной окружности.
+
-
 
+
-
42.&nbsp;&nbsp;&nbsp; Шкив имеет в диаметре 1,4 м и делает 80 оборотов в минуту. Найдите скорость точки на окружности шкива.
+
43. Найдите длину дуги окружности радиуса 1 см, отвечающей центральному углу:  
43. Найдите длину дуги окружности радиуса 1 см, отвечающей центральному углу:  
-
1) 30°; 2) 45°; 3) 120°; 4) 270°.
+
1) 30°; 2) 45°; 3) 120°; 4) 270°.  
-
[[Image:29-06-12.jpg]]
+
[[Image:29-06-12.jpg|480px|Окружности]]  
-
44.&nbsp;&nbsp;&nbsp; Сколько градусов содержит центральный угол, если соответствующая ему дуга составляет: [[Image:29-06-13.jpg]]<br>[[Image:29-06-14.jpg]]
+
44. Сколько градусов содержит центральный угол, если соответствующая ему дуга составляет: [[Image:29-06-13.jpg|120px|Задание]]<br>[[Image:29-06-14.jpg|120px|Задание]]  
-
&nbsp;окружности?
+
&nbsp;окружности?  
-
45.&nbsp;&nbsp;&nbsp; Какой угол образуют радиусы Земли, проведенные в две точки на ее поверхности, расстояние между которыми равно 1 км? Радиус Земли равен 6370 км.
+
45. Какой [[Угол. Прямой и развернутый угол. Чертежный треугольник|угол]] образуют радиусы Земли, проведенные в две точки на ее поверхности, расстояние между которыми равно 1 км? Радиус Земли равен 6370 км.  
-
46.&nbsp;&nbsp;&nbsp; По радиусу R=1 м найдите длину дуги, отвечающей центральному углу:
+
46. По радиусу R=1 м найдите длину дуги, отвечающей центральному углу:  
-
1) 45°; 2) 30°; 3) 120°; 4) 45°45';5)&nbsp;&nbsp;&nbsp; 60°30'; 6) 150°36'.
+
1) 45°; 2) 30°; 3) 120°; 4) 45°45';5)&nbsp;&nbsp;&nbsp; 60°30'; 6) 150°36'.  
-
47.&nbsp;&nbsp;&nbsp; По данной хорде а найдите длину ее дуги, если градусная мера дуги равна:
+
47. По данной хорде а найдите длину ее дуги, если градусная мера дуги равна:1) 60°; 2) 90°; 3) 120°.
-
1) 60°; 2) 90°; 3) 120°.
+
48. По данной длине дуги l найдите ее хорду, если дуга содержит:1) 60°; 2) 90°; 3) 120°.  
-
48.&nbsp;&nbsp;&nbsp; По данной длине дуги l найдите ее хорду, если дуга содержит:
+
49. Найдите радианную меру углов:1) 30°; 2) 45°; 3) 60°.
-
1) 60°; 2) 90°; 3) 120°.
+
50. Найдите радианную меру углов треугольника ABC, если [[Image:20-06-61.jpg]]A = 60°, [[Image:20-06-61.jpg]]B=45°.  
-
49.&nbsp;&nbsp;&nbsp; Найдите радианную меру углов:
+
51. Найдите градусную меру угла, если его радианная мера равна:  
-
1) 30°; 2) 45°; 3) 60°.
+
[[Image:29-06-15.jpg|320px|Задание]]&nbsp;  
-
50.&nbsp;&nbsp;&nbsp; Найдите радианную меру углов треугольника ABC, если [[Image:20-06-61.jpg]]A = 60°, [[Image:20-06-61.jpg]]B=45°.
+
<br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
-
51.&nbsp;&nbsp;&nbsp; Найдите градусную меру угла, если его радианная мера равна:
+
<br>  
-
 
+
-
[[Image:29-06-15.jpg]]<br><br><br>&nbsp;
+
-
 
+
-
<br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>  
+
<sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 9 класса [[Математика|скачать]]</sub>  
<sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 9 класса [[Математика|скачать]]</sub>  
Строка 136: Строка 128:
  '''<u>Содержание урока</u>'''
  '''<u>Содержание урока</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока                      '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока                      '''
-
  [[Image:1236084776 kr.jpg|10x10px]] опорный каркас   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас   
-
  [[Image:1236084776 kr.jpg|10x10px]] презентация урока
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
-
  [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы  
-
  [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии  
   
   
  '''<u>Практика</u>'''
  '''<u>Практика</u>'''
-
  [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения  
-
  [[Image:1236084776 kr.jpg|10x10px]] самопроверка
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
-
  [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
-
  [[Image:1236084776 kr.jpg|10x10px]] домашние задания
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
-
  [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
-
  [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
-
 
+
  '''<u>Иллюстрации</u>'''
  '''<u>Иллюстрации</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
-
  [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки  
-
  [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
-
  [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
-
  [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
   
   
  '''<u>Дополнения</u>'''
  '''<u>Дополнения</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
-
  [[Image:1236084776 kr.jpg|10x10px]] статьи  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи  
-
  [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных  
-
  [[Image:1236084776 kr.jpg|10x10px]] шпаргалки  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки  
-
  [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
-
  [[Image:1236084776 kr.jpg|10x10px]] словарь терминов                           
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов                           
-
  [[Image:1236084776 kr.jpg|10x10px]] прочие  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие  
  '''<u></u>'''
  '''<u></u>'''
  <u>Совершенствование учебников и уроков
  <u>Совершенствование учебников и уроков
-
  </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
+
  </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
-
  [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике  
-
  [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке  
-
  [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми  
-
 
+
  '''<u>Только для учителей</u>'''
  '''<u>Только для учителей</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
-
  [[Image:1236084776 kr.jpg|10x10px]] календарный план на год   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год   
-
  [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации   
-
  [[Image:1236084776 kr.jpg|10x10px]] программы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
-
  [[Image:1236084776 kr.jpg|10x10px]] обсуждения
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
   
   
   
   

Текущая версия на 12:30, 11 октября 2012

Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Задачи-3(9-класс)


Задачи

1. Даны две окружности с радиусами R1 и R2 и расстоянием между центрами d > R1 + R2. Чему равны наибольшее и наименьшее расстояния между точками X и У этих окружностей?

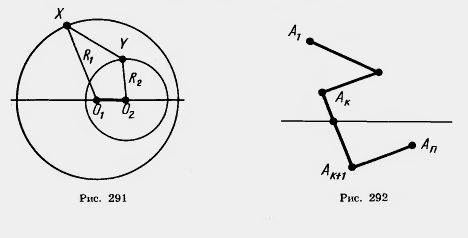
2. Решите задачу 1 при условии, что d<.R1 - R2 (рис. 291).

3. Докажите, что если вершины ломаной не лежат на одной прямой, то длина ломаной больше длины отрезка, соединяющего ее концы.

4. Докажите, что у замкнутой ломаной расстояние между любыми двумя вершинами не больше половины длины ломаной.

5. Докажите, что у замкнутой ломаной длина каждого звена не больше суммы длин остальных звеньев.

6. Может ли замкнутая ломаная иметь звенья длиной 1 м, 2 м, 3 м, 4 м, 11 м? Объясните ответ.

7. Докажите, что если концы ломаной лежат по разные стороны от данной прямой, то она пересекает эту прямую (рис. 292).

8. Сколько диагоналей у n-угольника?

9. Чему равна сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине?

Окружность. Ломаная
   
10. Углы выпуклого четырехугольника пропорциональны числам 1, 2, 3, 4. Найдите их.

11. Докажите, что у четырехугольника, описанного около окружности, суммы длин противолежащих сторон равны.

12. Сколько сторон имеет правильный многоугольник, каждый  из   внутренних   углов   которого   равен:

1) 135°; 2) 150°?

13. Сколько сторон имеет правильный многоугольник, если каждый из внешних его углов равен:

1) 36°; 2) 24°?

14. Докажите, что взятые через одну вершины правильного 2n-угольника являются вершинами правильного n-угольника.

15. Докажите, что середины сторон правильного n-угольника являются вершинами другого правильного n-угольника.

16. Найдите выражения для стороны аn правильного n-угольника через радиус R описанной около него окружности и радиус r вписанной окружности. Вычислите аn при n = 3, 4, 6.

17. Хорда, перпендикулярная радиусу и проходящая через его середину, равна стороне правильного вписанного треугольника. Докажите.

18. У правильного треугольника радиус вписанной окружности в два раза меньше радиуса описанной окружности. Докажите.

19. Сторона правильного вписанного в окружность треугольника равна а. Найдите сторону квадрата, вписанного в эту окружность.

20. В окружность, радиус которой 4 дм, вписан правильный треугольник, на стороне которого построен квадрат. Найдите радиус окружности, описанной около квадрата.

21. Конец валика диаметром 4 см опилен под квадрат. Каким может быть наибольший размер стороны квадрата?

22. Конец винта газовой задвижки имеет правильную трехгранную форму. Каким Может быть наибольший размер грани, если диаметр цилиндрической части винта 2 см?

23. Докажите, что сторона правильного 8-угольника вычисляется по формуле 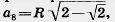Формула где R — радиус описанной окружности.
24. Докажите, что сторона правильного 12-угольника вычисляется по формуле 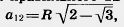Формула где R — радиус описанной окружности.

25*. Найдите стороны правильного пятиугольника и правильного 10-угольника, вписанных в окружность радиуса R.

26. Сторона правильного многоугольника равна а, а радиус описанной окружности R. Найдите радиус вписанной окружности.

27. Сторона правильного многоугольника равна а, а радиус вписанной окружности r. Найдите радиус описанной окружности.

28. Выразите сторону b правильного описанного многоугольника через радиус R окружности и сторону а правильного вписанного многоугольника с тем же числом сторон.

29. Выразите сторону а правильного вписанного многоугольника через радиус R окружности и сторону b правильного описанного многоугольника с тем же числом сторон.

30. Впишите в окружность правильный 12-угольник.

31. Опишите около окружности правильный треугольник, квадрат, правильный восьмиугольник.

32. Радиусы вписанной и описанной окружностей одного правильного n-угольника равны r1 и R1, а радиус вписанной окружности другого правильного n-угольника равен r2. Чему равен радиус описанной окружности другого n-угольника?

33. Периметры двух правильных n-угольников относятся как а: b. Как относятся радиусы их вписанных и описанных окружностей?

34. Вычислите длину окружности, если радиус равен:1) 10 м; 2) 15 м.

35. На сколько изменится длина окружности, если радиус изменится на 1 мм?

36. Найдите отношение периметра правильного вписанного 8-угольника к диаметру и сравните его с приближенным значением 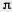24-06-93.jpg.

37. Решите задачу 36 для правильного 12-угольника.

38. Найдите радиус земного шара, исходя из того, что 1 м составляет одну 40-миллионную долю длины экватора.

39. На сколько удлинился бы земной экватор, если бы радиус земного шара увеличился на 1 см?

40. Внутри окружности радиуса R расположены п равных окружностей, которые касаются друг друга и данной окружности. Найдите радиус этих окружностей, если число их равно:1) 3; 2) 4; 3) 6 (рис. 293).

41. Решите предыдущую задачу, если окружности расположены вне данной окружности.

42. Шкив имеет в диаметре 1,4 м и делает 80 оборотов в минуту. Найдите скорость точки на окружности шкива.

43. Найдите длину дуги окружности радиуса 1 см, отвечающей центральному углу:

1) 30°; 2) 45°; 3) 120°; 4) 270°.

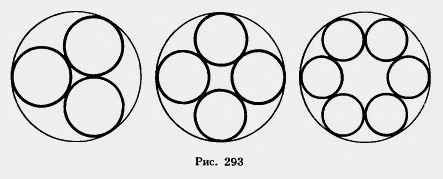
Окружности

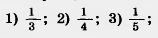
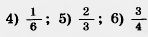
44. Сколько градусов содержит центральный угол, если соответствующая ему дуга составляет: Задание
Задание

 окружности?

45. Какой угол образуют радиусы Земли, проведенные в две точки на ее поверхности, расстояние между которыми равно 1 км? Радиус Земли равен 6370 км.

46. По радиусу R=1 м найдите длину дуги, отвечающей центральному углу:

1) 45°; 2) 30°; 3) 120°; 4) 45°45';5)    60°30'; 6) 150°36'.

47. По данной хорде а найдите длину ее дуги, если градусная мера дуги равна:1) 60°; 2) 90°; 3) 120°.

48. По данной длине дуги l найдите ее хорду, если дуга содержит:1) 60°; 2) 90°; 3) 120°.

49. Найдите радианную меру углов:1) 30°; 2) 45°; 3) 60°.

50. Найдите радианную меру углов треугольника ABC, если 20-06-61.jpgA = 60°, 20-06-61.jpgB=45°.

51. Найдите градусную меру угла, если его радианная мера равна:

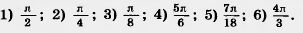
Задание 


А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений


Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 9 класса скачать 


Содержание урока
1236084776 kr.jpg конспект урока                       
1236084776 kr.jpg опорный каркас  
1236084776 kr.jpg презентация урока
1236084776 kr.jpg акселеративные методы 
1236084776 kr.jpg интерактивные технологии 

Практика
1236084776 kr.jpg задачи и упражнения 
1236084776 kr.jpg самопроверка
1236084776 kr.jpg практикумы, тренинги, кейсы, квесты
1236084776 kr.jpg домашние задания
1236084776 kr.jpg дискуссионные вопросы
1236084776 kr.jpg риторические вопросы от учеников

Иллюстрации
1236084776 kr.jpg аудио-, видеоклипы и мультимедиа 
1236084776 kr.jpg фотографии, картинки 
1236084776 kr.jpg графики, таблицы, схемы
1236084776 kr.jpg юмор, анекдоты, приколы, комиксы
1236084776 kr.jpg притчи, поговорки, кроссворды, цитаты

Дополнения
1236084776 kr.jpg рефераты
1236084776 kr.jpg статьи 
1236084776 kr.jpg фишки для любознательных 
1236084776 kr.jpg шпаргалки 
1236084776 kr.jpg учебники основные и дополнительные
1236084776 kr.jpg словарь терминов                          
1236084776 kr.jpg прочие 

Совершенствование учебников и уроков
1236084776 kr.jpg исправление ошибок в учебнике
1236084776 kr.jpg обновление фрагмента в учебнике 
1236084776 kr.jpg элементы новаторства на уроке 
1236084776 kr.jpg замена устаревших знаний новыми 

Только для учителей
1236084776 kr.jpg идеальные уроки 
1236084776 kr.jpg календарный план на год  
1236084776 kr.jpg методические рекомендации  
1236084776 kr.jpg программы
1236084776 kr.jpg обсуждения


Интегрированные уроки


Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B8-3(9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81)»

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: