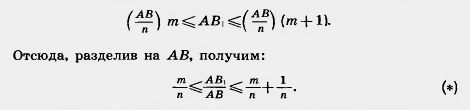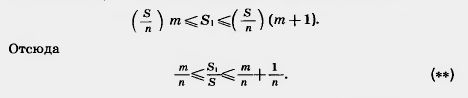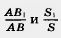|
|
| (1 промежуточная версия не показана) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Алгебра, урок, на Тему, Площадь прямоугольника</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Площадь прямоугольника, площадь, прямоугольника, квадрат</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Площадь прямоугольника''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Площадь прямоугольника''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА''' | + | '''Площадь прямоугольника''' |
| | | | |
| - | <br>Найдем площадь прямоугольника со сторонами а, b. Для этого сначала докажем, что площади двух прямоугольников с равными основаниями относятся как их высоты. | + | <br>Найдем [[Понятие площади|площадь]] прямоугольника со сторонами а, b. Для этого сначала докажем, что площади двух прямоугольников с равными основаниями относятся как их высоты. |
| | | | |
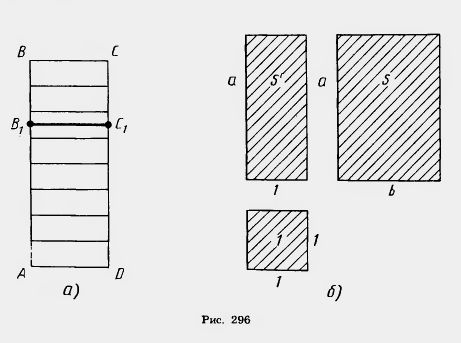
| - | Пусть ABCD и AB<sub>1</sub>C<sub>1</sub>D — два прямоугольника с общим основанием AD (рис. 296, а). Пусть S и S<sub>1</sub> — их площади. Докажем, что | + | Пусть ABCD и AB<sub>1</sub>C<sub>1</sub>D — два прямоугольника с общим основанием AD (рис. 296, а). Пусть S и S<sub>1</sub> — их площади. Докажем, что |
| | | | |
| - | [[Image:29-06-17.jpg]] | + | [[Image:29-06-17.jpg|80px|Формула]] |
| | | | |
| - | Разобьем сторону АВ прямоугольника на большое число n равных частей, каждая из них равна [[Image:29-06-18.jpg]] Пусть m — число точек деления, которые лежат на стороне АВ<sub>1</sub>. Тогда | + | Разобьем сторону АВ [[Акселеративна вправа до уроку на тему «Прямокутник. Задачі на знаходження третього додатка. Знаходження значень буквених виразів»|прямоугольника]] на большое число n равных частей, каждая из них равна [[Image:29-06-18.jpg]] Пусть m — число точек деления, которые лежат на стороне АВ<sub>1</sub>. Тогда |
| | | | |
| - | [[Image:29-06-19.jpg]] | + | [[Image:29-06-19.jpg|480px|Формула]] |
| | | | |
| - | Проведем через точки деления прямые, параллельные основанию AD. Они разобьют прямоугольник ABCD на n равных прямоугольников. Каждый из них имеет площадь [[Image:29-06-20.jpg]] Прямоугольник AB<sub>1</sub>C<sub>1</sub>D содержит первые т прямоугольников, считая снизу, и содержится в m +1 прямоугольниках. Поэтому | + | Проведем через точки деления прямые, параллельные основанию AD. Они разобьют прямоугольник ABCD на n равных прямоугольников. Каждый из них имеет площадь [[Image:29-06-20.jpg]] Прямоугольник AB<sub>1</sub>C<sub>1</sub>D содержит первые т прямоугольников, считая снизу, и содержится в m +1 прямоугольниках. Поэтому |
| | | | |
| - | [[Image:29-06-21.jpg]]<br><br>Из неравенств (*) и (**) мы видим, что оба числа [[Image:29-06-22.jpg]] заключичены между [[Image:29-06-23.jpg]] . Поэтому они отличаются не более чем | + | [[Image:29-06-21.jpg|480px|Формула]]<br><br>Из неравенств (*) и (**) мы видим, что оба числа [[Image:29-06-22.jpg|80px|Формула]] заключичены между [[Image:29-06-23.jpg|80px|Формула]] . Поэтому они отличаются не более чем<br> |
| | | | |
| | + | [[Image:29-06-24.jpg|480px|Площадь прямоугольника]] <br> <br>на [[Image:29-06-25.jpg]]. А так как n можно взять сколь угодно большим, то это может быть только при [[Image:29-06-26.jpg|80px|Формула]], что и требовалось доказать. |
| | | | |
| | + | Возьмем теперь [[Ромб i його властивості, квадрат i його властивості|квадрат]], являющийся единицей площади, прямоугольник со сторонами 1, а и прямоугольник со сторонами а, b (рис. 296, б). Сравнивая их площади, по доказанному будем иметь: |
| | | | |
| - | [[Image:29-06-24.jpg]]<br> <br> <br>на [[Image:29-06-25.jpg]]. А так как n можно взять сколь угодно большим, то это может быть только при [[Image:29-06-26.jpg]], что и требовалось доказать.<br><br>Возьмем теперь квадрат, являющийся единицей площади, прямоугольник со сторонами 1, а и прямоугольник со сторонами а, b (рис. 296, б). Сравнивая их площади, по доказанному будем иметь: | + | [[Image:29-06-27.jpg|120px|Формула]]<br><br>Перемножая эти равенства почленно, получим:S = ab. |
| | | | |
| - | [[Image:29-06-27.jpg]]<br><br>Перемножая эти равенства почленно, получим:
| + | Итак, площадъ прямоугольника со сторонами а, b вычисляется по формуле S=ab. |
| | | | |
| - | S = ab.
| + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Итак, плогцадъ прямоугольника со сторонами а, b вычисляется по формуле S=ab.<br><br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Математика за 9 класс бесплатно [[Математика|скачать]], планы конспектов уроков, готовимся к школе [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Математика за 9 класс бесплатно [[Математика|скачать]], планы конспектов уроков, готовимся к школе [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 38: |
Строка 38: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Проведем через точки деления прямые, параллельные основанию AD. Они разобьют прямоугольник ABCD на n равных прямоугольников. Каждый из них имеет площадь 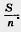 Прямоугольник AB1C1D содержит первые т прямоугольников, считая снизу, и содержится в m +1 прямоугольниках. Поэтому
Прямоугольник AB1C1D содержит первые т прямоугольников, считая снизу, и содержится в m +1 прямоугольниках. Поэтому
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.