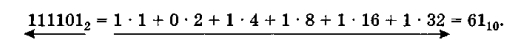|
|
|
| (6 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Информатика, 6 класс, Двоичное кодирование числовой информации</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Информатика, 6 класс, Двоичное кодирование числовой информации, клавиши, калькулятор, двоичный код</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика ]]>>[[Информатика 6 класс|Информатика 6 класс]]>> Двоичное кодирование числовой информации''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика ]]>>[[Информатика 6 класс|Информатика 6 класс]]>> Двоичное кодирование числовой информации''' |
| | | | |
| | + | <br> <br> |
| | | | |
| - | <br>
| + | ''' Двоичное '''[[Как кодируется изображение|'''кодирование''']]''' числовой информации''' |
| | | | |
| - | Двоичное '''[[Как кодируется изображение|кодирование]]'''
| + | <br> Известно множество способов записи чисел. Мы пользуемся десятичной позиционной системой счисления. |
| - | числовой информации<br><br>Известно множество способов записи чисел. Мы пользуемся десятичной позиционной системой счисления.
| + | |
| | | | |
| - | Десятичной она называется потому, что в этой системе счисления десять единиц одного разряда составляют одну единицу следующего старшего разряда. Число 10 называется основанием десятичной системы счисления. Для записи чисел в десятичной системе счисления используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. | + | Десятичной она называется потому, что в этой системе счисления десять единиц одного разряда составляют одну единицу следующего старшего разряда. Число 10 называется основанием десятичной системы счисления. Для записи чисел в десятичной системе счисления используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. |
| | | | |
| - | Позиционной эта система счисления называется потому, что одна и та же цифра получает различные количественные значения в зависимости от места, или позиции, которую она занимает в записи числа. Например, в записи числа 555 цифра 5, стоящая на первом месте справа, обозначает 5 единиц, на втором — 5 десятков, на третьем — 5 сотен. | + | Позиционной эта система счисления называется потому, что одна и та же цифра получает различные количественные значения в зависимости от места, или позиции, которую она занимает в записи числа. Например, в записи числа 555 цифра 5, стоящая на первом месте справа, обозначает 5 единиц, на втором — 5 десятков, на третьем — 5 сотен. |
| | | | |
| - | Рассмотрим два числовых ряда: | + | Рассмотрим два числовых ряда: |
| | | | |
| - | 1, 10, 100, 1000, 10 000, 100 000 ...<br>1, 2, 4, 8, 16, 32, 64, 12В, 256, 512, 1024, 2048 ...<br><br>Оба этих ряда начинаются с единицы. Каждое следующее число первого ряда получается путем умножения предыдущего числа на 10. Каждое следующее число второго ряда получается путем умножения предыдущего числа на 2. | + | 1, 10, 100, 1000, 10 000, 100 000 ...<br>1, 2, 4, 8, 16, 32, 64, 12В, 256, 512, 1024, 2048 ...<br><br>Оба этих ряда начинаются с единицы. Каждое следующее число первого ряда получается путем умножения предыдущего числа на 10. Каждое следующее число второго ряда получается путем умножения предыдущего числа на 2. |
| | | | |
| - | Любое целое число можно представить в виде суммы разрядных слагаемых — единиц, десятков, сотен, тысяч и так далее, записанных в первом ряду. При этом каждый член этого ряда может либо не входить в сумму, либо входить в нее от 1 до 9 раз. Пример: | + | Любое целое число можно представить в виде суммы разрядных слагаемых — единиц, десятков, сотен, тысяч и так далее, записанных в первом ряду. При этом каждый член этого ряда может либо не входить в [http://xvatit.com/busines/ '''сумму'''], либо входить в нее от 1 до 9 раз. Пример: |
| | | | |
| - | 1409 = 1 • 1000 + 4 • 100 + О • 10 + 9 • 1. | + | 1409 = 1 • 1000 + 4 • 100 + О • 10 + 9 • 1. |
| | | | |
| - | Числа 1, 4, 0, 9, на которые умножаются члены первого ряда, составляют исходное число 1409. | + | Числа 1, 4, 0, 9, на которые умножаются члены первого ряда, составляют исходное число 1409. |
| | | | |
| - | Перевод целых десятичных чисел в двоичный код <br><br><u>Способ 1</u><br><br>Попробуем представить число 1409 в виде суммы членов второго ряда. | + | Перевод целых десятичных чисел в '''[[В мире кодов|двоичный код]]''' <br><br><u>Способ 1</u><br><br>Попробуем представить число 1409 в виде суммы членов второго ряда. |
| | | | |
| - | Воспользуемся методом разностей. Возьмем ближайший к исходному числу, но не превосходящий его член второго ряда и составим разность:<br><br>1409 - 1024 = 385.<br><br>Возьмем ближайший к полученной разности, но не превосходящий ее член второго ряда и составим разность:<br><br>385 - 256 = 129.<br><br>Аналогично составим разность:<br><br>129 - 128 = 1.<br><br>В итоге получим:<br><br>1409 = 1024 + 256 + 128 + 1 = 1 • 1024 + 0 • 512 + 1 • 256 + 1 • 128 + 0 • 64 + 0 • 32 + 0 • 16 + 0 • 8 + 0 • 4 + 0 • 2 + 1 • 1.<br><br>Мы видим, что каждый член второго ряда может либо не входить в сумму, либо входить в нее только один раз. <br><br>карт<br><br>Числа 1 и 0, на которые умножаются члены второго ряда, также составляют исходное число 1409, но в его другой, двоичной записи: 10110000001.<br><br>Результат записывают так:<br><br>140910 = 101100000012.<br><br>Исходное число мы записали с помощью 0 и 1, другими словами, получили двоичный код этого числа, или представили число в двоичной системе счисления.<br><br><u>Способ 2</u><br><br>Этот способ получения двоичного кода десятичного числа основан на записи остатков от деления исходного числа и получаемых частных на 2, продолжаемого до тех пор, пока очередное частное не окажется равным 0. | + | Воспользуемся методом разностей. Возьмем ближайший к исходному числу, но не превосходящий его член второго ряда и составим разность:<br><br>1409 - 1024 = 385.<br><br>Возьмем ближайший к полученной разности, но не превосходящий ее член второго ряда и составим разность:<br><br>385 - 256 = 129.<br><br>Аналогично составим разность:<br><br>129 - 128 = 1.<br><br>В итоге получим:<br><br>1409 = 1024 + 256 + 128 + 1 = 1 • 1024 + 0 • 512 + 1 • 256 + 1 • 128 + 0 • 64 + 0 • 32 + 0 • 16 + 0 • 8 + 0 • 4 + 0 • 2 + 1 • 1.<br><br>Мы видим, что каждый член второго ряда может либо не входить в сумму, либо входить в нее только один раз. <br><br>[[Image:15-03-06.jpg|550px|Весы]]<br><br>Числа 1 и 0, на которые умножаются члены второго ряда, также составляют исходное число 1409, но в его другой, двоичной записи: 10110000001.<br><br>Результат записывают так:<br><br>1409<sub>10</sub> = 10110000001<sub>2</sub>.<br><br>Исходное число мы записали с помощью 0 и 1, другими словами, получили двоичный код этого числа, или представили число в двоичной системе счисления.<br><br><u>Способ 2</u><br><br>Этот способ получения двоичного кода десятичного числа основан на записи остатков от деления исходного числа и получаемых частных на 2, продолжаемого до тех пор, пока очередное частное не окажется равным 0. |
| | | | |
| - | Пример:<br><br>карт <br><br>В первую ячейку верхней строки записано исходное число, а в каждую следующую — результат целочисленного деления предыдущего числа на 2. | + | Пример:<br><br>[[Image:15-03-07.jpg|550px|Способ получения двоичного кода]]<br><br>В первую ячейку верхней строки записано исходное число, а в каждую следующую — результат целочисленного деления предыдущего числа на 2. |
| | | | |
| - | В ячейках нижней строки записаны остатки от деления стоящих в верхней строке чисел на 2. | + | В ячейках нижней строки записаны остатки от деления стоящих в верхней строке чисел на 2. |
| | | | |
| - | Последняя ячейка нижней строки остается пустой. Двоичный код исходного десятичного числа получается при последовательной записи всех остатков, начиная с последнего: 140910 = 101100000012. | + | Последняя ячейка нижней строки остается пустой. Двоичный код исходного десятичного числа получается при последовательной записи всех остатков, начиная с последнего: 1409<sub>10 </sub>= 10110000001<sub>2</sub>. |
| | | | |
| | Первые 20 членов натурального ряда в двоичной системе счисления записываются так: 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110,1111, 10000, 10001, 10010, 10011, 10100. | | Первые 20 членов натурального ряда в двоичной системе счисления записываются так: 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110,1111, 10000, 10001, 10010, 10011, 10100. |
| | | | |
| - | Перевод целых чисел из двоичной системы счисления в десятичную<br><br><u>Способ 1</u><br><br>Пусть имеется число 1111012. Его можно представить так:<br><br>карт<br><br><u>Способ 2</u><br><br>Возьмем то же число 1111012. Переведем единицу 0-го разряда (первая слева в записи числа) в единицы 5-го разряда, для чего 1 умножим на 2, ибо единица 6-го разряда в двоичной системе содержит 2 единицы 5-го разряда. | + | '' Перевод целых чисел из двоичной системы счисления в десятичную''<br><br><u>Способ 1</u><br><br>Пусть имеется число 1111012. Его можно представить так:<br><br>[[Image:15-03-08.jpg|550px|Пример]]<br><br><u>Способ 2</u><br><br>Возьмем то же число 1111012. Переведем единицу 0-го разряда (первая слева в записи числа) в единицы 5-го разряда, для чего 1 умножим на 2, ибо единица 6-го разряда в двоичной системе содержит 2 единицы 5-го разряда. |
| | | | |
| - | К полученным 2 единицам 5-го разряда прибавим имеющуюся единицу 5-го разряда. Переведем эти 3 единицы 5-го разряда в 4-й разряд и прибавим имеющуюся единицу 4-го разряда: 3 • 2 + 1 = 7. | + | К полученным 2 единицам 5-го разряда прибавим имеющуюся единицу 5-го разряда. Переведем эти 3 единицы 5-го разряда в 4-й разряд и прибавим имеющуюся единицу 4-го разряда: 3 • 2 + 1 = 7. |
| | | | |
| - | Переведем 7 единиц 4-го разряда в 3-й разряд и прибавим имеющуюся единицу 3-го разряда: 7 • 2 + 1 = 15. | + | Переведем 7 единиц 4-го разряда в 3-й разряд и прибавим имеющуюся единицу 3-го разряда: 7 • 2 + 1 = 15. |
| | | | |
| - | Переведем 15 единиц 3-го разряда во 2-й разряд: 15 • 2 = 30. В исходном числе во 2-м разряде единиц нет. | + | Переведем 15 единиц 3-го разряда во 2-й разряд: 15 • 2 = 30. В исходном числе во 2-м разряде единиц нет. |
| | | | |
| - | Переведем 30 единиц 2-го разряда в 1-й разряд и прибавим имеющуюся там единицу: 30 • 2 + 1 = 61. Мы получили, что исходное число содержит 61 единицу 1-го разряда. Письменные вычисления удобно располагать так:<br><br>((((1 • 2 + 1) • 2 + 1) • 2 + 1) • 2 + 0) • 2 + 1 = 61.<br><br>Переводить целые числа из десятичной системы счисления в двоичную систему счисления и обратно можно с помощью приложения '''[[Конспект уроку на тему «Робота з Калькулятором і вікнами»|Калькулятор]]'''. | + | Переведем 30 единиц 2-го разряда в 1-й разряд и прибавим имеющуюся там единицу: 30 • 2 + 1 = 61. Мы получили, что исходное число содержит 61 единицу 1-го разряда. Письменные вычисления удобно располагать так:<br><br>((((1 • 2 + 1) • 2 + 1) • 2 + 1) • 2 + 0) • 2 + 1 = 61.<br><br>Переводить целые числа из десятичной системы счисления в двоичную систему счисления и обратно можно с помощью приложения '''[[Конспект уроку на тему «Робота з Калькулятором і вікнами»|Калькулятор]]'''. |
| | | | |
| - | Проведем небольшой эксперимент. | + | Проведем небольшой эксперимент. |
| | | | |
| - | 1. Запустите приложение Калькулятор и выполните команду [Вид-Инженерный]. Обратите внимание на группу переключателей, определяющих систему счисления:<br><br>карт<br><br>2. Убедитесь, что Калькулятор настроен на работу в десятичной системе счисления. С помощью клавиатуры или мыши введите в поле ввода произвольное двузначное число. Активизируйте переключатель Bin и проследите за изменениями в окне ввода. Вернитесь в десятичную систему счисления. Очистите поле ввода. | + | 1. Запустите приложение Калькулятор и выполните команду [Вид-Инженерный]. Обратите внимание на группу переключателей, определяющих систему счисления:<br><br>[[Image:15-03-09.jpg|550px|Приложение Калькулятор]]<br><br>2. Убедитесь, что Калькулятор настроен на работу в десятичной системе счисления. С помощью клавиатуры или мыши введите в поле ввода произвольное двузначное число. Активизируйте переключатель Bin и проследите за изменениями в окне ввода. Вернитесь в десятичную систему счисления. Очистите поле ввода. |
| | | | |
| - | 3. Повторите пункт 2 несколько раз для других десятичных чисел. | + | 3. Повторите пункт 2 несколько раз для других десятичных чисел. |
| | | | |
| - | 4. Настройте Калькулятор на работу в двоичной системе счисления. Обратите внимание на то, какие кнопки Калькулятора и цифровые '''[[Справочный материал|клавиши]]''' клавиатуры вам доступны. Поочередно введите двоичные коды 5-го, 10-го и 15-го членов натурального ряда и с помощью переключателя Dec переведите их в десятичную систему счисления. | + | 4. Настройте Калькулятор на работу в двоичной системе счисления. Обратите внимание на то, какие кнопки Калькулятора и цифровые '''[[Справочный материал|клавиши]]''' клавиатуры вам доступны. Поочередно введите двоичные коды 5-го, 10-го и 15-го членов натурального ряда и с помощью переключателя Dec переведите их в десятичную систему счисления. |
| | | | |
| | В главе 4 «Материал для любознательных» вы можете узнать много интересных сведений из истории счета и систем счисления.<br><br><br><br> | | В главе 4 «Материал для любознательных» вы можете узнать много интересных сведений из истории счета и систем счисления.<br><br><br><br> |
| - |
| |
| - | <br>
| |
| | | | |
| | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.'' | | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.'' |
| Строка 62: |
Строка 60: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82_%D1%83%D1%80%D0%BE%D0%BA%D0%B0_%D0%BD%D0%B0_%D1%82%D0%B5%D0%BC%D1%83:_%D0%9F%D1%83%D1%82%D0%B5%D1%88%D0%B5%D1%81%D1%82%D0%B2%D0%B8%D0%B5_%D0%B2_%D0%BC%D0%B8%D1%80_%D0%BA%D0%BE%D0%B4%D0%BE%D0%B2 опорный каркас] |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%94%D0%B2%D0%BE%D0%B8%D1%87%D0%BD%D0%BE%D0%B5_%D0%BA%D0%BE%D0%B4%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%BE%D0%B2%D0%BE%D0%B9_%D0%B8%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%86%D0%B8%D0%B8._%D0%9F%D1%80%D0%B5%D0%B7%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F_%D1%83%D1%80%D0%BE%D0%BA%D0%B0 презентация урока] |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9A%D0%BE%D0%B4%D1%83%D0%B2%D0%B0%D0%BD%D0%BD%D1%8F._%D0%9F%D1%80%D0%B0%D0%BA%D1%82%D0%B8%D0%BA%D1%83%D0%BC%D0%B8,_%D0%BB%D0%B0%D0%B1%D0%BE%D1%80%D0%B0%D1%82%D0%BE%D1%80%D0%BD%D1%96,_%D0%BA%D0%B5%D0%B9%D1%81%D0%B8 задачи и упражнения] |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| Строка 77: |
Строка 75: |
| | | | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| Строка 84: |
Строка 82: |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| Строка 91: |
Строка 89: |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| - | '''<u></u>''' | + | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' | | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| Строка 99: |
Строка 97: |
| | | | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
Текущая версия на 08:51, 16 октября 2012
Гипермаркет знаний>>Информатика >>Информатика 6 класс>> Двоичное кодирование числовой информации
Двоичное кодирование числовой информации
Известно множество способов записи чисел. Мы пользуемся десятичной позиционной системой счисления.
Десятичной она называется потому, что в этой системе счисления десять единиц одного разряда составляют одну единицу следующего старшего разряда. Число 10 называется основанием десятичной системы счисления. Для записи чисел в десятичной системе счисления используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Позиционной эта система счисления называется потому, что одна и та же цифра получает различные количественные значения в зависимости от места, или позиции, которую она занимает в записи числа. Например, в записи числа 555 цифра 5, стоящая на первом месте справа, обозначает 5 единиц, на втором — 5 десятков, на третьем — 5 сотен.
Рассмотрим два числовых ряда:
1, 10, 100, 1000, 10 000, 100 000 ...
1, 2, 4, 8, 16, 32, 64, 12В, 256, 512, 1024, 2048 ...
Оба этих ряда начинаются с единицы. Каждое следующее число первого ряда получается путем умножения предыдущего числа на 10. Каждое следующее число второго ряда получается путем умножения предыдущего числа на 2.
Любое целое число можно представить в виде суммы разрядных слагаемых — единиц, десятков, сотен, тысяч и так далее, записанных в первом ряду. При этом каждый член этого ряда может либо не входить в сумму, либо входить в нее от 1 до 9 раз. Пример:
1409 = 1 • 1000 + 4 • 100 + О • 10 + 9 • 1.
Числа 1, 4, 0, 9, на которые умножаются члены первого ряда, составляют исходное число 1409.
Перевод целых десятичных чисел в двоичный код
Способ 1
Попробуем представить число 1409 в виде суммы членов второго ряда.
Воспользуемся методом разностей. Возьмем ближайший к исходному числу, но не превосходящий его член второго ряда и составим разность:
1409 - 1024 = 385.
Возьмем ближайший к полученной разности, но не превосходящий ее член второго ряда и составим разность:
385 - 256 = 129.
Аналогично составим разность:
129 - 128 = 1.
В итоге получим:
1409 = 1024 + 256 + 128 + 1 = 1 • 1024 + 0 • 512 + 1 • 256 + 1 • 128 + 0 • 64 + 0 • 32 + 0 • 16 + 0 • 8 + 0 • 4 + 0 • 2 + 1 • 1.
Мы видим, что каждый член второго ряда может либо не входить в сумму, либо входить в нее только один раз.
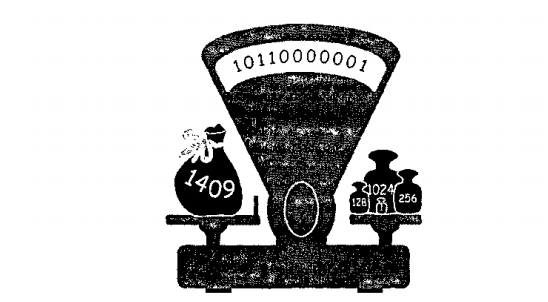
Числа 1 и 0, на которые умножаются члены второго ряда, также составляют исходное число 1409, но в его другой, двоичной записи: 10110000001.
Результат записывают так:
140910 = 101100000012.
Исходное число мы записали с помощью 0 и 1, другими словами, получили двоичный код этого числа, или представили число в двоичной системе счисления.
Способ 2
Этот способ получения двоичного кода десятичного числа основан на записи остатков от деления исходного числа и получаемых частных на 2, продолжаемого до тех пор, пока очередное частное не окажется равным 0.
Пример:
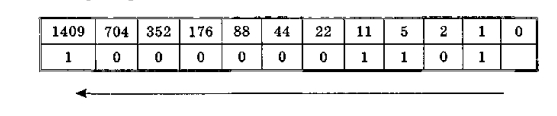
В первую ячейку верхней строки записано исходное число, а в каждую следующую — результат целочисленного деления предыдущего числа на 2.
В ячейках нижней строки записаны остатки от деления стоящих в верхней строке чисел на 2.
Последняя ячейка нижней строки остается пустой. Двоичный код исходного десятичного числа получается при последовательной записи всех остатков, начиная с последнего: 140910 = 101100000012.
Первые 20 членов натурального ряда в двоичной системе счисления записываются так: 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110,1111, 10000, 10001, 10010, 10011, 10100.
Перевод целых чисел из двоичной системы счисления в десятичную
Способ 1
Пусть имеется число 1111012. Его можно представить так:
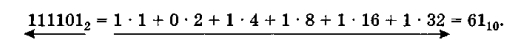
Способ 2
Возьмем то же число 1111012. Переведем единицу 0-го разряда (первая слева в записи числа) в единицы 5-го разряда, для чего 1 умножим на 2, ибо единица 6-го разряда в двоичной системе содержит 2 единицы 5-го разряда.
К полученным 2 единицам 5-го разряда прибавим имеющуюся единицу 5-го разряда. Переведем эти 3 единицы 5-го разряда в 4-й разряд и прибавим имеющуюся единицу 4-го разряда: 3 • 2 + 1 = 7.
Переведем 7 единиц 4-го разряда в 3-й разряд и прибавим имеющуюся единицу 3-го разряда: 7 • 2 + 1 = 15.
Переведем 15 единиц 3-го разряда во 2-й разряд: 15 • 2 = 30. В исходном числе во 2-м разряде единиц нет.
Переведем 30 единиц 2-го разряда в 1-й разряд и прибавим имеющуюся там единицу: 30 • 2 + 1 = 61. Мы получили, что исходное число содержит 61 единицу 1-го разряда. Письменные вычисления удобно располагать так:
((((1 • 2 + 1) • 2 + 1) • 2 + 1) • 2 + 0) • 2 + 1 = 61.
Переводить целые числа из десятичной системы счисления в двоичную систему счисления и обратно можно с помощью приложения Калькулятор.
Проведем небольшой эксперимент.
1. Запустите приложение Калькулятор и выполните команду [Вид-Инженерный]. Обратите внимание на группу переключателей, определяющих систему счисления:

2. Убедитесь, что Калькулятор настроен на работу в десятичной системе счисления. С помощью клавиатуры или мыши введите в поле ввода произвольное двузначное число. Активизируйте переключатель Bin и проследите за изменениями в окне ввода. Вернитесь в десятичную систему счисления. Очистите поле ввода.
3. Повторите пункт 2 несколько раз для других десятичных чисел.
4. Настройте Калькулятор на работу в двоичной системе счисления. Обратите внимание на то, какие кнопки Калькулятора и цифровые клавиши клавиатуры вам доступны. Поочередно введите двоичные коды 5-го, 10-го и 15-го членов натурального ряда и с помощью переключателя Dec переведите их в десятичную систему счисления.
В главе 4 «Материал для любознательных» вы можете узнать много интересных сведений из истории счета и систем счисления.
Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|