|
|
|
| (5 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Информатика, 6 класс, Ханойская башня, или один замечательный алгоритм</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Информатика, 6 класс, Ханойская башня, или один замечательный алгоритм, калькулятор, алгорим, таблица</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика ]]>>[[Информатика 6 класс|Информатика 6 класс]]>> Ханойская башня, или один замечательный алгоритм''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика ]]>>[[Информатика 6 класс|Информатика 6 класс]]>> Ханойская башня, или один замечательный алгоритм'''<br><br>Одна из древних легенд гласит: «В непроходимых джунглях недалеко от города Ханоя есть храм бога Брамы. В нем находится бронзовая плита с тремя алмазными стержнями. На один из стержней бог при сотворении мира нанизал 64 диска разных диаметров из чистого золота. Наибольший диск лежит на бронзовой плите, а остальные образуют пирамиду, сужающуюся кверху. Это башня Брамы. Работая день и ночь, жрецы храма переносят диски с одного стержня на другой, следуя законам Брамы: |
| | | | |
| - | <br> | + | 1) диски можно перемещать с одного стержня на другой только по одному;<br>2) нельзя класть больший диск на меньший;<br>3) нельзя откладывать диски в сторону, при переносе дисков с одного стержня на другой можно использовать промежуточный третий стержень, на котором диски должны находиться тоже только в виде пирамиды, сужающейся кверху. |
| | + | |
| | + | Когда все 64 диска будут перенесены с одного стержня на другой, наступит конец света». |
| | + | |
| | + | Эта древняя легенда положена в основу задачи о Ханойской башне: переместить n дисков со стержня 1 на стержень 3, используя промежуточный стержень 2 и соблюдая законы Брамы.<br> <br>[[Image:16-03-017.jpg|550px|задачи о Ханойской башне]]<br><br>Если башня состоит из одного диска, то она переносится за один ход: 1->3. |
| | + | |
| | + | Башня из двух дисков переносится за три хода: 1—>2, 1—>3, 2—>3. |
| | + | |
| | + | Для переноса башни из трех дисков потребуется уже семь ходов: 1->3, 1->2, 3->2, 1->3, 2->1, 2->3, 1->3. Обратите внимание, за первые три хода мы переносим башню из двух верхних дисков на второй промежуточный стержень. Затем переносим самый большой диск с первого стержня на третий и еще раз проделываем хорошо знакомую нам операцию: переносим башню из двух дисков на третий диск. |
| | + | |
| | + | Следовательно, чтобы перенести башню из четырех дисков с первого стержня на третий, необходимо действовать по плану: |
| | + | |
| | + | 1) перенести башню из трех верхних дисков с первого стержня на второй (7 ходов);<br>2) самый большой диск перенести с первого стержня на третий (1 ход);<br>3) перенести башню из трех дисков со второго стержня на третий (7 ходов). |
| | + | |
| | + | Всего на перенос потребуется 15 ходов. |
| | + | |
| | + | Рассуждая аналогичным образом, сосчитаем число ходов, необходимых для переноса башни из пяти дисков: <br><br>15 + 1 + 15 = 2 • 15 + 1 = 31.<br><br>Для башни из 6 дисков получаем: 2 • 31 + 1 = 63 и т. д. <br><br>Рассмотренный нами '''[[Что такое алгоритм|Алгоритм]]''' решения задачи «Ханойская башня» обладает одним удивительным свойством: в ходе его выполнения для башни, состоящей из n колец, мы используем алгоритм для чуть более простой ситуации — переноса башни, состоящей из n - 1 кольца. В свою очередь, в алгоритме для башни из n - 1 кольца используется этот же алгоритм для n - 2 колец и т. д. |
| | + | |
| | + | Прием, когда некоторый процесс описывается через самого себя, называется рекурсией. '''[[Что такое алгоритм|Алгоритм]]''' решения задачи «Ханойская башня» — пример рекурсивного алгоритма.<br><br>'''Вопросы и задания'''<br><br>''1. Проведите необходимые вычисления и заполните следующую '''[[Табличные модели|таблицу]]''':''<br> |
| | + | |
| | + | {| cellspacing="1" cellpadding="1" border="1" style="width: 330px; height: 234px;" |
| | + | |- |
| | + | | Число дисков |
| | + | | Число ходов |
| | + | |- |
| | + | | 7 |
| | + | | |
| | + | |- |
| | + | | 8 |
| | + | | |
| | + | |- |
| | + | | 9 |
| | + | | |
| | + | |- |
| | + | | 10 |
| | + | | |
| | + | |- |
| | + | | 20 |
| | + | | 1 048 575 |
| | + | |- |
| | + | | 21 |
| | + | | |
| | + | |- |
| | + | | 30 |
| | + | | |
| | + | |- |
| | + | | 31 |
| | + | | |
| | + | |- |
| | + | | 39 |
| | + | | |
| | + | |- |
| | + | | 40 |
| | + | | 1 099 511 627 775 |
| | + | |} |
| | + | |
| | + | ''<br>2. Назовите числа: 1048 575,1073 741823,1 099 511627 775. Что это за числа?'' |
| | | | |
| - | § 4.12. Ханойская башня, или один замечательный алгоритм<br><br>Одна из древних легенд гласит: «В непроходимых джунглях недалеко от города Ханоя есть храм бога Брамы. В нем находится бронзовая плита с тремя алмазными стержнями. На один из стержней бог при сотворении мира нанизал 64 диска разных диаметров из чистого золота. Наибольший диск лежит на бронзовой плите, а остальные образуют пирамиду, сужающуюся кверху. Это башня Брамы. Работая день и ночь, жрецы храма переносят диски с одного стержня на другой, следуя законам Брамы:<br><br>1) диски можно перемещать с одного стержня на другой только по одному;<br>2) нельзя класть больший диск на меньший;<br>3) нельзя откладывать диски в сторону, при переносе дисков с одного стержня на другой можно использовать промежуточный третий стержень, на котором диски должны находиться тоже только в виде пирамиды, сужающейся кверху.<br><br>Когда все 64 диска будут перенесены с одного стержня на другой, наступит конец света».<br><br>Эта древняя легенда положена в основу задачи о Ханойской башне: переместить п дисков со стержня 1 на стержень 3, используя промежуточный стержень 2 и соблюдая законы Брамы.<br> <br>карт <br><br>Если башня состоит из одного диска, то она переносится за один ход: 1->3.<br><br>Башня из двух дисков переносится за три хода: 1—>2, 1—>3, 2—>3.<br><br>Для переноса башни из трех дисков потребуется уже семь ходов: 1->3, 1->2, 3->2, 1->3, 2->1, 2->3, 1->3. Обратите внимание, за первые три хода мы переносим башню из двух верхних дисков на второй промежуточный стержень. Затем переносим самый большой диск с первого стержня на третий и еще раз проделываем хорошо знакомую нам операцию: переносим башню из двух дисков на третий диск.<br><br>Следовательно, чтобы перенести башню из четырех дисков с первого стержня на третий, необходимо действовать по плану:<br><br>1) перенести башню из трех верхних дисков с первого стержня на второй (7 ходов);<br>2) самый большой диск перенести с первого стержня на третий (1 ход);<br>3) перенести башню из трех дисков со второго стержня на третий (7 ходов).<br><br>Всего на перенос потребуется 15 ходов. <br><br>Рассуждая аналогичным образом, сосчитаем число ходов, необходимых для переноса башни из пяти дисков: <br><br>15 + 1 + 15 = 2 • 15 + 1 = 31.<br><br>Для башни из 6 дисков получаем: 2 • 31 + 1 = 63 и т. д. <br><br>Рассмотренный нами алгоритм решения задачи «Ханойская башня» обладает одним удивительным свойством: в ходе его выполнения для башни, состоящей из n колец, мы используем алгоритм для чуть более простой ситуации — переноса башни, состоящей из n - 1 кольца. В свою очередь, в алгоритме для башни из n - 1 кольца используется этот же алгоритм для n - 2 колец и т. д.<br><br>Прием, когда некоторый процесс описывается через самого себя, называется рекурсией. Алгоритм решения задачи «Ханойская башня» — пример рекурсивного алгоритма.<br><br>Вопросы и задания<br><br>1. Проведите необходимые вычисления и заполните следующую таблицу:<br><br>табл<br><br>Число дисков Число ходов<br><br>7 <br>8 <br>9 <br>10 <br>20 1 048 575<br>21 <br>30 1 073 741 823<br>31 <br>39 <br>40 1 099 511 627 775<br><br>2. Назовите числа: 1048 575,1073 741823,1 099 511627 775. Что это за числа?<br><br>3. Для того чтобы переместить башню из 64 дисков, при безошибочной работе потребуется 18 446 744 073 709 551 615 перекладываний. Сколько уйдет на это времени, если считать, что на одно перекладывание уходит одна секунда? Для выполнения вычислений используйте приложение Калькулятор. <br><br><br><br><br>
| + | ''3. Для того чтобы переместить башню из 64 дисков, при безошибочной [http://xvatit.com/busines/ '''работе'''] потребуется 18 446 744 073 709 551 615 перекладываний. Сколько уйдет на это времени, если считать, что на одно перекладывание уходит одна секунда? Для выполнения вычислений используйте приложение '''''[[Конспект уроку на тему «Робота з Калькулятором і вікнами»|Калькулятор]]'''. <br><br><br> |
| | | | |
| | <br> | | <br> |
| Строка 11: |
Строка 67: |
| | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.'' | | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.'' |
| | | | |
| - | <br> <br>
| + | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%A5%D0%B0%D0%BD%D0%BE%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D0%B1%D0%B0%D1%88%D0%BD%D1%8F,_%D0%B8%D0%BB%D0%B8_%D0%BE%D0%B4%D0%B8%D0%BD_%D0%B7%D0%B0%D0%BC%D0%B5%D1%87%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC._%D0%9F%D1%80%D0%B5%D0%B7%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F_%D1%83%D1%80%D0%BE%D0%BA%D0%B0 презентация урока] |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| Строка 29: |
Строка 85: |
| | | | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] [http://school.xvatit.com/index.php?title=%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%A5%D0%B0%D0%BD%D0%BE%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D0%B1%D0%B0%D1%88%D0%BD%D1%8F,_%D0%B8%D0%BB%D0%B8_%D0%BE%D0%B4%D0%B8%D0%BD_%D0%B7%D0%B0%D0%BC%D0%B5%D1%87%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC._%D0%93%D1%80%D0%B0%D1%84%D0%B8%D0%BA%D0%B8,_%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D1%8B,_%D1%81%D1%85%D0%B5%D0%BC%D1%8B графики, таблицы, схемы] |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| Строка 43: |
Строка 99: |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| - | '''<u></u>''' | + | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' | | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| Строка 51: |
Строка 107: |
| | | | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации | | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
Текущая версия на 13:58, 31 октября 2012
Гипермаркет знаний>>Информатика >>Информатика 6 класс>> Ханойская башня, или один замечательный алгоритм
Одна из древних легенд гласит: «В непроходимых джунглях недалеко от города Ханоя есть храм бога Брамы. В нем находится бронзовая плита с тремя алмазными стержнями. На один из стержней бог при сотворении мира нанизал 64 диска разных диаметров из чистого золота. Наибольший диск лежит на бронзовой плите, а остальные образуют пирамиду, сужающуюся кверху. Это башня Брамы. Работая день и ночь, жрецы храма переносят диски с одного стержня на другой, следуя законам Брамы:
1) диски можно перемещать с одного стержня на другой только по одному;
2) нельзя класть больший диск на меньший;
3) нельзя откладывать диски в сторону, при переносе дисков с одного стержня на другой можно использовать промежуточный третий стержень, на котором диски должны находиться тоже только в виде пирамиды, сужающейся кверху.
Когда все 64 диска будут перенесены с одного стержня на другой, наступит конец света».
Эта древняя легенда положена в основу задачи о Ханойской башне: переместить n дисков со стержня 1 на стержень 3, используя промежуточный стержень 2 и соблюдая законы Брамы.
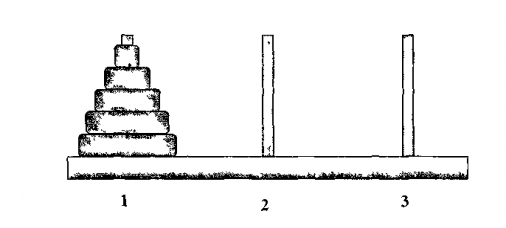
Если башня состоит из одного диска, то она переносится за один ход: 1->3.
Башня из двух дисков переносится за три хода: 1—>2, 1—>3, 2—>3.
Для переноса башни из трех дисков потребуется уже семь ходов: 1->3, 1->2, 3->2, 1->3, 2->1, 2->3, 1->3. Обратите внимание, за первые три хода мы переносим башню из двух верхних дисков на второй промежуточный стержень. Затем переносим самый большой диск с первого стержня на третий и еще раз проделываем хорошо знакомую нам операцию: переносим башню из двух дисков на третий диск.
Следовательно, чтобы перенести башню из четырех дисков с первого стержня на третий, необходимо действовать по плану:
1) перенести башню из трех верхних дисков с первого стержня на второй (7 ходов);
2) самый большой диск перенести с первого стержня на третий (1 ход);
3) перенести башню из трех дисков со второго стержня на третий (7 ходов).
Всего на перенос потребуется 15 ходов.
Рассуждая аналогичным образом, сосчитаем число ходов, необходимых для переноса башни из пяти дисков:
15 + 1 + 15 = 2 • 15 + 1 = 31.
Для башни из 6 дисков получаем: 2 • 31 + 1 = 63 и т. д.
Рассмотренный нами Алгоритм решения задачи «Ханойская башня» обладает одним удивительным свойством: в ходе его выполнения для башни, состоящей из n колец, мы используем алгоритм для чуть более простой ситуации — переноса башни, состоящей из n - 1 кольца. В свою очередь, в алгоритме для башни из n - 1 кольца используется этот же алгоритм для n - 2 колец и т. д.
Прием, когда некоторый процесс описывается через самого себя, называется рекурсией. Алгоритм решения задачи «Ханойская башня» — пример рекурсивного алгоритма.
Вопросы и задания
1. Проведите необходимые вычисления и заполните следующую таблицу:
| Число дисков
| Число ходов
|
| 7
|
|
| 8
|
|
| 9
|
|
| 10
|
|
| 20
| 1 048 575
|
| 21
|
|
| 30
|
|
| 31
|
|
| 39
|
|
| 40
| 1 099 511 627 775
|
2. Назовите числа: 1048 575,1073 741823,1 099 511627 775. Что это за числа?
3. Для того чтобы переместить башню из 64 дисков, при безошибочной работе потребуется 18 446 744 073 709 551 615 перекладываний. Сколько уйдет на это времени, если считать, что на одно перекладывание уходит одна секунда? Для выполнения вычислений используйте приложение Калькулятор.
Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











