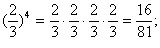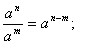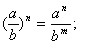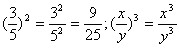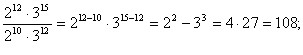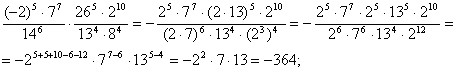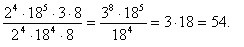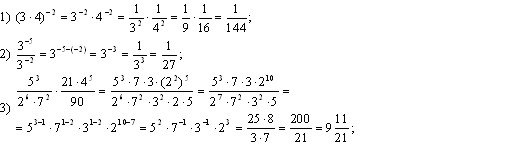|
|
| (18 промежуточных версий не показаны.) |
| Строка 1: |
Строка 1: |
| | <metakeywords>Гіпермаркет Знань - перший в світі!, Гіпермаркет Знань, Математика, 7 клас, Тема 7, Степінь з натуральним показником, Властивості степеня</metakeywords> | | <metakeywords>Гіпермаркет Знань - перший в світі!, Гіпермаркет Знань, Математика, 7 клас, Тема 7, Степінь з натуральним показником, Властивості степеня</metakeywords> |
| | | | |
| - | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 7 клас. Повні уроки|Математика 7 клас. Повні уроки]]>> АЛГЕБРА: Степінь з натуральним показником. Властивості степеня. Повні уроки''' | + | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 7 клас. Повні уроки|Математика 7 клас. Повні уроки]]>> Алгебра: Степінь з натуральним показником. Властивості степеня. Повні уроки'''<br> |
| | | | |
| - | <br> '''АЛГЕБРА'''<br>
| + | ==Тема== |
| | + | *'''Степінь з натуральним показником. Властивості степеня. Повні уроки''' |
| | | | |
| - | <br>
| + | ==Мета== |
| - | | + | |
| - | <u>'''Тема 7. Степінь з натуральним показником. Властивості степеня'''</u><br>
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | <br> <!--[if !mso]>
| + | |
| - | <style>
| + | |
| - | v\:* {behavior:url(#default#VML);}
| + | |
| - | o\:* {behavior:url(#default#VML);}
| + | |
| - | w\:* {behavior:url(#default#VML);}
| + | |
| - | .shape {behavior:url(#default#VML);}
| + | |
| - | </style>
| + | |
| - | <![endif]--><!--[if gte mso 9]><xml>
| + | |
| - | <w:WordDocument>
| + | |
| - | <w:View>Normal</w:View>
| + | |
| - | <w:Zoom>0</w:Zoom>
| + | |
| - | <w:PunctuationKerning/>
| + | |
| - | <w:ValidateAgainstSchemas/>
| + | |
| - | <w:SaveIfXMLInvalid>false</w:SaveIfXMLInvalid>
| + | |
| - | <w:IgnoreMixedContent>false</w:IgnoreMixedContent>
| + | |
| - | <w:AlwaysShowPlaceholderText>false</w:AlwaysShowPlaceholderText>
| + | |
| - | <w:Compatibility>
| + | |
| - | <w:BreakWrappedTables/>
| + | |
| - | <w:SnapToGridInCell/>
| + | |
| - | <w:WrapTextWithPunct/>
| + | |
| - | <w:UseAsianBreakRules/>
| + | |
| - | <w:DontGrowAutofit/>
| + | |
| - | </w:Compatibility>
| + | |
| - | <w:BrowserLevel>MicrosoftInternetExplorer4</w:BrowserLevel>
| + | |
| - | </w:WordDocument>
| + | |
| - | </xml><![endif]--><!--[if gte mso 9]><xml>
| + | |
| - | <w:LatentStyles DefLockedState="false" LatentStyleCount="156">
| + | |
| - | </w:LatentStyles>
| + | |
| - | </xml><![endif]--><!--[if gte mso 10]>
| + | |
| - | <style>
| + | |
| - | /* Style Definitions */
| + | |
| - | table.MsoNormalTable
| + | |
| - | {mso-style-name:"Обычная таблица";
| + | |
| - | mso-tstyle-rowband-size:0;
| + | |
| - | mso-tstyle-colband-size:0;
| + | |
| - | mso-style-noshow:yes;
| + | |
| - | mso-style-parent:"";
| + | |
| - | mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
| + | |
| - | mso-para-margin:0cm;
| + | |
| - | mso-para-margin-bottom:.0001pt;
| + | |
| - | mso-pagination:widow-orphan;
| + | |
| - | font-size:10.0pt;
| + | |
| - | font-family:"Times New Roman";
| + | |
| - | mso-ansi-language:#0400;
| + | |
| - | mso-fareast-language:#0400;
| + | |
| - | mso-bidi-language:#0400;}
| + | |
| - | </style>
| + | |
| - | <![endif]--><!--[if gte mso 9]><xml>
| + | |
| - | <o:shapedefaults v:ext="edit" spidmax="1027"/>
| + | |
| - | </xml><![endif]--><!--[if gte mso 9]><xml>
| + | |
| - | <o:shapelayout v:ext="edit">
| + | |
| - | <o:idmap v:ext="edit" data="1"/>
| + | |
| - | </o:shapelayout></xml><![endif]-->
| + | |
| - | | + | |
| - | ''<span lang="UK" style="color: black;">7. Степінь з
| + | |
| - | натуральним показником. Властивості степеня</span>''
| + | |
| - | | + | |
| - | ''<span lang="UK" style="color: black;"> </span>''
| + | |
| - | | + | |
| - | <span lang="UK" style="color: black;">Мета: дізнатися, що таке степінь. Виокремити основні його властивості.
| + | |
| - | Навчитися розв’язувати задачі із степенем.</span>
| + | |
| - | | + | |
| - | <span lang="UK" style="color: black;">План:</span>
| + | |
| - | | + | |
| - | '''<span lang="UK" style="font-size: 11.5pt; color: black;">1. Степінь натурального числа з натуральним
| + | |
| - | показником</span>'''<span lang="UK" style="color: black;" />
| + | |
| - | | + | |
| - | '''<span lang="UK" style="font-size: 11.5pt; color: black;">2. Степінь дійсного числа з натуральним показником</span>'''<span lang="UK" style="color: black;" />
| + | |
| - | | + | |
| - | '''<span lang="UK" style="font-size: 11.5pt; color: black;">3. Властивості степеня дійсного числа з натуральним
| + | |
| - | показником</span>'''<span lang="UK" style="font-size: 11.5pt; color: black;"> </span>
| + | |
| - | | + | |
| - | '''<span lang="UK" style="font-size: 11.5pt; color: black;">4. Степінь дійсного числа з нульовим і цілим
| + | |
| - | від'ємним показником.</span>'''<span lang="UK" style="font-size: 11.5pt; color: black;">
| + | |
| - | | + | |
| - | | + | |
| - | | + | |
| - | </span>''<span lang="UK" style="color: black;" />''
| + | |
| | | | |
| - | ''<span lang="UK" style="color: black;"> </span>''
| + | *дізнатися, що таке степінь. |
| | + | *Виокремити основні його властивості. |
| | + | *Навчитися розв’язувати задачі із степенем. |
| | | | |
| - | '''''<span lang="UK" style="font-size: 11.5pt; color: black;">1.
| + | ==План== |
| - | Степінь натурального числа з натуральним показником</span>'''''<span lang="UK" style="font-size: 11.5pt; color: black;">
| + | |
| | | | |
| | + | 1. Степінь натурального числа з натуральним показником<br>2. Степінь дійсного числа з натуральним показником<br>3. Властивості степеня дійсного числа з натуральним показником <br>4. Степінь дійсного числа з нульовим і цілим від'ємним показником.<br> |
| | | | |
| | + | ===Степінь натурального числа з натуральним показником=== |
| | | | |
| - | Степенем називається добуток кількох рівних множників. | + | [[Степінь з натуральним показником. Властивості степеня|Степенем]] називається добуток кількох рівних множників. |
| | | | |
| | Наприклад, | | Наприклад, |
| | | | |
| - | 3•3=3<sup>2</sup> – другий степінь числа 3, або квадрат числа 3; | + | 3•3=3<sup>2</sup> – другий степінь числа 3, або квадрат числа 3; <br>х•х•х=х<sup>3</sup> – третій степінь змінної х, або куб змінної х; <br>с•с•с•с•с=с<sup>5</sup> – п'ятий степінь змінної с; |
| | | | |
| - | х•х•х=х<sup>3</sup> – третій степінь змінної х, або куб змінної х;
| + | Піднести число 2 до третього степеня – означає перемножити три двійки, тобто 2<sup>3</sup>=2•2•2=8. |
| | | | |
| - | с•с•с•с•с=с<sup>5</sup> – п'ятий степінь змінної с;
| + | <br>Число яке підносять до степеня – [[Вирази зі степенями|основа степеня]], число яке показує до якого степеня підноситься основа – показник степеня. |
| | | | |
| - | Піднести число 2 до третього степеня – означає перемножити три двійки, тобто 2<sup>3</sup>=2•2•2=8.
| + | <br>Першим степенем числа домовились вважати саме це число: а<sup>1</sup> – те саме число, що й а. Показник 1 не прийнято писати. <br><br>{{#ev:youtube|AiBOGC1EDgM}} |
| | | | |
| | + | ===Степінь дійсного числа з натуральним показником=== |
| | | | |
| - | Число яке підносять до степеня – основа степеня, число яке показує до якого
| + | Поняття степеня натурального числа з натуральним показником узагальнюється на степінь дійсного числа з натуральним показником: |
| - | степеня підноситься основа – показник степеня.
| + | |
| | | | |
| - | Першим степенем числа домовились вважати саме це число: а<sup>1</sup> – те саме
| + | <br><u>а<sup>n</sup> = а•а•а…а. </u> |
| - | число, що й а. Показник 1 не прийнято писати.
| + | |
| | | | |
| - | | + | <br>Будь-який степінь додатного числа є число додатне. |
| - | | + | |
| - | </span> | + | |
| - | | + | |
| - | <span lang="UK" style="font-size: 11.5pt; color: black;">[http://interneturok.ru/video/algebra/7_klass/stepen_s_naturalnym_pokazatelem_i_eyo_svojstva/chto_takoe_stepen_s_naturalnym_pokazatelem/ http://interneturok.ru/video/algebra/7_klass/stepen_s_naturalnym_pokazatelem_i_eyo_svojstva/chto_takoe_stepen_s_naturalnym_pokazatelem/]</span>
| + | |
| - | | + | |
| - | <span lang="UK" style="font-size: 11.5pt; color: black;">
| + | |
| - | | + | |
| - | 2'''''. Степінь дійсного числа з натуральним показником'''''
| + | |
| - | | + | |
| - | | + | |
| - | | + | |
| - | Поняття степеня натурального числа з натуральним показником узагальнюється на
| + | |
| - | степінь дійсного числа з натуральним показником:
| + | |
| - | | + | |
| - | а<sup>n</sup> = <u>а•а•а…а</u>.
| + | |
| - | | + | |
| - | Будь-який степінь додатного числа є число додатне. | + | |
| | | | |
| | Парний степінь від'ємного числа – число додатне. | | Парний степінь від'ємного числа – число додатне. |
| Строка 139: |
Строка 42: |
| | Непарний степінь від'ємного числа – число від'ємне. | | Непарний степінь від'ємного числа – число від'ємне. |
| | | | |
| - | ''Приклади:''
| + | <br>Приклади: |
| | | | |
| - | [[Image:]] | + | [[Image:1801-26.jpg|200px|Вирази]]<br> <br>2) (-0,2)<sup>3</sup>=(-0,2)•(-0,2)•(-0,2)=-0,008; |
| | | | |
| - | 2) (-0,2)<sup>3</sup>=(-0,2)•(-0,2)•(-0,2)=-0,008;
| + | 3) Знайти [[Вирази зі змінними. Цілі раціональні вирази. Повні уроки|значення виразу]] |
| - | | + | |
| - | 3) Знайти значення виразу | + | |
| | | | |
| | 5а<sup>2</sup>+27:(а-1)<sup>3</sup>, якщо а= -2. | | 5а<sup>2</sup>+27:(а-1)<sup>3</sup>, якщо а= -2. |
| Строка 151: |
Строка 52: |
| | Розв'язання. Якщо а= -2, то значення даного виразу дорівнює | | Розв'язання. Якщо а= -2, то значення даного виразу дорівнює |
| | | | |
| - | 5•(-2)<sup>2</sup>+27:(-3)<sup>3</sup>=5•4+27:(-27)=20-1=19. | + | 5•(-2)<sup>2</sup>+27:(-3)<sup>3</sup>=5•4+27:(-27)=20-1=19. <br> |
| - | | + | |
| - | | + | |
| - | | + | |
| - | '''''3. Властивості степеня дійсного числа з натуральним показником'''''
| + | |
| - | | + | |
| - | | + | |
| - | | + | |
| - | 1) Основна властивість степеня:
| + | |
| - | | + | |
| - | Яке б не було а і натуральні показники степенів m і n, завжди
| + | |
| - | | + | |
| - | а<sup>m</sup> • а<sup>n</sup>=а<sup>m+n</sup>.
| + | |
| | | | |
| | + | ===Властивості степеня дійсного числа з натуральним показником=== |
| | | | |
| | + | <br>1) [[Вирази зі степенями. Вправи та задачі|Основна властивість степеня]]: |
| | | | |
| - | З основної властивості степеня випливає: | + | Яке б не було а і натуральні показники степенів m і n, завжди <br>а<sup>m</sup> • а<sup>n</sup>=а<sup>m+n</sup>. <br><br>'''З основної властивості степеня випливає''' |
| | | | |
| - | При множенні степенів з однаковою основою показники степенів додають, а основу | + | При множенні степенів з однаковою основою показники степенів додають, а основу залишають ту ж саму. |
| - | залишають ту ж саму. | + | |
| | | | |
| | Приклади. 3<sup>2</sup>•3<sup>8</sup>=3<sup>10</sup>; | | Приклади. 3<sup>2</sup>•3<sup>8</sup>=3<sup>10</sup>; |
| Строка 176: |
Строка 66: |
| | 1,2<sup>3</sup>•1,2<sup>4</sup>=1,2<sup>7</sup>; | | 1,2<sup>3</sup>•1,2<sup>4</sup>=1,2<sup>7</sup>; |
| | | | |
| - | х<sup>5</sup>•х<sup>8</sup>=х13; | + | х<sup>5</sup>•х<sup>8</sup>=х<sup>13</sup>; <br><br>2) При діленні степенів з однаковою основою показники степенів віднімають, а основу залишають ту ж саму. |
| | | | |
| | + | [[Image:1801-27.jpg|100px|Вирази]]<br> <br>Приклади. |
| | | | |
| - | | + | [[Image:1801-28.jpg|200px|Вирази]]<br> <br>3) Яке б не було а і натуральні показники степеня m і n, завжди |
| - | 2) При діленні степенів з однаковою основою показники степенів віднімають, а
| + | |
| - | основу залишають ту ж саму.
| + | |
| - | | + | |
| - | [[Image:]] | + | |
| - | | + | |
| - | Приклади.
| + | |
| - | | + | |
| - | [[Image:]]
| + | |
| - | | + | |
| - | 3) Яке б не було а і натуральні показники степеня m і n, завжди | + | |
| | | | |
| | (а<sup>n</sup>) <sup>m</sup>=а<sup>nm</sup>. | | (а<sup>n</sup>) <sup>m</sup>=а<sup>nm</sup>. |
| | | | |
| - | Щоб піднести степінь до степеня, потрібно показники степенів перемножити, а | + | Щоб піднести степінь до степеня, потрібно показники степенів перемножити, а основу залишити ту саму. |
| - | основу залишити ту саму. | + | |
| | | | |
| | (а<sup>n</sup>)<sup>m</sup>=а<sup>nm</sup>=(а <sup>m</sup>) <sup>n</sup>; | | (а<sup>n</sup>)<sup>m</sup>=а<sup>nm</sup>=(а <sup>m</sup>) <sup>n</sup>; |
| Строка 204: |
Строка 84: |
| | (х<sup>5</sup>)<sup>8</sup>=х<sup>40</sup>; | | (х<sup>5</sup>)<sup>8</sup>=х<sup>40</sup>; |
| | | | |
| - | 4) Щоб піднести добуток до степеня, потрібно кожен з множників піднести до | + | <br>4) Щоб піднести добуток до степеня, потрібно кожен з множників піднести до степеня. |
| - | степеня. | + | |
| | | | |
| | (ас) <sup>n</sup>=а <sup>n</sup>•с <sup>n</sup>; | | (ас) <sup>n</sup>=а <sup>n</sup>•с <sup>n</sup>; |
| | | | |
| - | Цю формулу часто застосовують в зворотньому порядку. | + | Цю формулу часто застосовують в зворотньому порядку. <br><br>Приклади. |
| - | | + | |
| - | | + | |
| - | | + | |
| - | ''Приклади. ''
| + | |
| | | | |
| | (2•3)<sup>2</sup>=2<sup>2</sup>•3<sup>2</sup>=4•9=36; | | (2•3)<sup>2</sup>=2<sup>2</sup>•3<sup>2</sup>=4•9=36; |
| | | | |
| - | (2х)<sup>3</sup>=2<sup>3</sup>•х<sup>3</sup>=8•х<sup>3</sup>; \ | + | (2х)<sup>3</sup>=2<sup>3</sup>•х<sup>3</sup>=8•х<sup>3</sup>; |
| | | | |
| - | 5<sup>3</sup>•3<sup>3</sup>=(5•<sup>3</sup>)<sup>3</sup>=15<sup>3</sup>=3375. | + | 5<sup>3</sup>•3<sup>3</sup>=(5•3)<sup>3</sup>=15<sup>3</sup>=3375. <br><br>Щоб піднести частку до степеня, потрібно кожен з множників піднести до степеня. |
| | | | |
| | + | [[Image:1801-29.jpg|100px|Вирази]]<br> Приклади: |
| | | | |
| - | | + | [[Image:1801-30.jpg|200px|Вирази]]<br> <br>5) Один в будь-якому степені дорівнює один. |
| - | Щоб піднести частку до степеня, потрібно кожен з множників піднести до степеня.
| + | |
| - | | + | |
| - | | + | |
| - | [[Image:]]
| + | |
| - | | + | |
| - | ''Приклади:''
| + | |
| - | | + | |
| - | [[Image:]] | + | |
| - | | + | |
| - | 5) Один в будь-якому степені дорівнює один. | + | |
| | | | |
| | 1<sup>n</sup>=1; | | 1<sup>n</sup>=1; |
| | | | |
| - | 6) Будь-яке число в першому степені дорівнює самому числу. | + | <br>6) Будь-яке число в першому степені дорівнює самому числу. |
| - | | + | |
| - | а<sup>1</sup>=а;
| + | |
| - | | + | |
| - | | + | |
| - | | + | |
| - | ''Зауваження.'' Розв´язуючи приклади, зручно скорочувати вирази, оскільки це
| + | |
| - | швидше приводить до результату.
| + | |
| - | | + | |
| - | | + | |
| - | | + | |
| - | ''Приклади.''
| + | |
| - | | + | |
| - | 1) [[Image:]]
| + | |
| - | | + | |
| - | 2) [[Image:]]
| + | |
| - | | + | |
| - | 3) [[Image:]]
| + | |
| - | | + | |
| - | | + | |
| | | | |
| - | '''''4. Степінь дійсного числа з нульовим і цілим від'ємним показником.''''' | + | а<sup>1</sup>=а; <br><br>'''Зауваження.''' |
| | | | |
| | + | Розв´язуючи приклади, зручно [[Тотожні вирази. Тотожні перетворення виразів. Презентація уроку|скорочувати вирази]], оскільки це швидше приводить до результату. <br><br>Приклади. |
| | | | |
| | + | <br>1) [[Image:1801-31.jpg|480px|Вирази]]<br>2) [[Image:1801-32.jpg|480px|Вирази]]<br>3) [[Image:1801-33.jpg|480px|Вирази]]<br> |
| | | | |
| | + | ===Степінь дійсного числа з нульовим і цілим від'ємним показником=== |
| | | | |
| - | Будь-яке число в нульовому степені дорівнює одиниці. | + | <br>Будь-яке число в нульовому степені дорівнює одиниці. |
| | | | |
| | а<sup>0</sup>=1. | | а<sup>0</sup>=1. |
| | | | |
| - | Щоб піднести число до від'ємного степеня потрібно одиницю поділити на це число | + | <br>Щоб піднести число до від'ємного степеня потрібно одиницю поділити на це число у додатному степені. |
| - | у додатному степені. | + | |
| | | | |
| - | а<sup>-n</sup>=1/а<sup>n</sup>. | + | а<sup>-n</sup>=1/<sup>аn</sup>. |
| | | | |
| - | Приклади. | + | <br>Приклади. <br> <br>[[Image:1801-34.jpg|480px|Вирази]] |
| | | | |
| - | [[Image:]]</span>'''<u><span lang="UK" style="color: black;" /></u>'''
| + | <br> |
| | | | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | [[Image:1801-35.jpg|480px|Вирази]] <br><br><br>7. До вашої уваги — кросворд. Ви повинні розгадати його і у виділеному стовпці прочитати назву найпершої весняної квітки, занесеної до Червоної книги.(Кросворд прикріпити на дошці і маркером вписувати слова, а букви, які утворять слово Підсніжник, написати червоним маркером) |
| | | | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | <br> |
| | | | |
| - | '''<u><span lang="UK" style="color: black;">[[Image:]]</span></u>'''
| + | [[Image:1801-36.jpg|240px|Кроссворд]] |
| | | | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>''' | + | <br>1. Як називається [[Тотожні вирази. Тотожні перетворення виразів. Повні уроки|вираз]] а<sup>n</sup>? (Степінь)<br>2. Показник степеня а <sup>-3</sup> число — ... (Від'ємне)<br>3. Основа степеня 2<sup>19</sup> число — ... (Два)<br>4. Який показник степеня a<sup>100</sup>? (Сто)<br>5. а° = .... (Один)<br>6. Напишіть замість «х» показник степеня а<sup>-10</sup> • а<sup>х</sup>=а<sup>-3</sup>(Сім)<br>7. Дано (m<sup>-3</sup>)<sup>-5</sup> = m <sup>15</sup>. Яку дію виконали над показниками, щоб піднести степінь до степеня? (Множення)<br>8. a<sup>-n</sup> *a<sup>n</sup>=... (Один)<br>9. Напишіть замість «х» показник степеня: с<sup>11</sup>:с<sup>8</sup>=с<sup>х</sup> (Три)<br>10. а<sup>3</sup> — число а у 3 степені. А як ще можна назвати цей вираз? (Куб)<br>Ключове слово: підсніжник.<br><br>{{#ev:youtube|Dvagp3IRNSo}}<br><br>{{#ev:youtube|nl6_2XjDm4c}}<br> |
| | | | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | ==Список використаної літератури== |
| | | | |
| - | '''<u><span lang="UK" style="color: black;">7. </span></u>'''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.15pt;">До вашої уваги — | + | ''1. Урок на тему «Тотожні вирази» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).<br>2. Урок на тему «Перетворення тотожних виразів» викладача Конченко Т. М. , [http://xvatit.com/vuzi/ Гімназії міжнародних відносин], м. Київ (СЗШ №323).<br>3. Істер О. А. «Алгебра.[[7_клас_уроки|7 клас]]».<br>4. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл. <br>5. Тарасов Валентин Алексеевич, учитель школы "Логос ЛВ", ст.преп. фак-та довузовской подготовки МИТХТ, г. Москва ''<br> |
| - | кросворд. Ви повинні розгадати </span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.25pt;">його і у виділеному стовпці прочитати назву
| + | |
| - | найпер</span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.15pt;">шої весняної квітки, занесеної до Червоної книги.(''Кросворд прикріпити на дошці і маркером вписувати слова, а букви, які
| + | |
| - | утворять слово Підсніжник, написати червоним маркером)''</span>
| + | |
| | | | |
| - | #[[Image:]]<span lang="UK" style="font-size: 11pt; letter-spacing: -0.25pt;">Як називається вираз ''а<sup>n</sup>?
| + | <br> |
| - | (Степінь)''</span><span lang="UK" style="font-size: 11pt; letter-spacing: -1.3pt;" />
| + | |
| | | | |
| - | ''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;"><span style="">2.<span style="font: 7pt "Times New Roman";">
| + | ---- |
| - | </span></span></span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.3pt;">Показник степеня ''а <sup>-3</sup> ''число
| + | |
| - | — ... ''(Від'ємне)''</span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;" />''
| + | |
| | | | |
| - | <span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;"><span style="">3.<span style="font: 7pt "Times New Roman";"> | + | <br>''Відредаговано і надіслано Мазуренко М.С.''<br> |
| - | </span></span></span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.25pt;">Основа степеня 2<sup>19</sup> число — ... ''(Два)''</span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;" />
| + | |
| | | | |
| - | <span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;"><span style="">4.<span style="font: 7pt "Times New Roman";">
| + | ---- |
| - | </span></span></span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.45pt;">Який показник степеня ''a''<sup>100</sup>? ''(Сто)''</span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;" />
| + | |
| | | | |
| - | <span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;"><span style="">5.<span style="font: 7pt "Times New Roman";"> | + | <br> '''Над уроком працювали''' |
| - | </span></span></span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.25pt;">а° = .... (Один)</span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;" />
| + | |
| | | | |
| - | #<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.4pt;">Напишіть замість «х» показник степеня а<sup>-10</sup>
| + | Конченко Т. М. |
| - | • а<sup>х</sup>=а<sup>-3</sup></span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.55pt;">(Сім)</span>''<span style="" />
| + | |
| - | #<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.2pt;">Дано (''m''<sup>-3</sup>)<sup>-5</sup> =</span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.2pt;"> </span>''''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.2pt;">m</span>''<sup><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.2pt;"> 15</span></sup><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.2pt;">. Яку
| + | |
| - | дію виконали над показ</span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.15pt;">никами, щоб піднести степінь до
| + | |
| - | степеня? ''(Мно''</span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.6pt;">ження)</span>''
| + | |
| | | | |
| - | <span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;"><span style="">8.<span style="font: 7pt "Times New Roman";">
| + | Мазуренко М.С. |
| - | </span></span></span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.25pt;">a<sup>-n</sup> *a<sup>n</sup>=... (Один)</span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;" />
| + | |
| - | | + | |
| - | <span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;"><span style="">9.<span style="font: 7pt "Times New Roman";">
| + | |
| - | </span></span></span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.4pt;">Напишіть замість «х» показник степеня</span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: 0.3pt;">:<span style=""> </span>с<sup>11</sup>:с<sup>8</sup>=с<sup>х</sup><span style=""> </span></span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.35pt;">(Три)</span>''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.8pt;" />
| + | |
| - | | + | |
| - | <span style=""><span style="">10.<span style="font: 7pt "Times New Roman";"> </span></span></span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.15pt;">а<sup>3</sup>
| + | |
| - | — число а у 3 степені. А як ще можна назвати </span><span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.25pt;">цей вираз? ''(Куб)''</span><span style="" />
| + | |
| - | | + | |
| - | ''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.4pt;">Ключове слово</span>'''''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.4pt;">: </span>''''''<span lang="UK" style="font-size: 11pt; color: black; letter-spacing: -0.4pt;">підсніжник.</span><u><span lang="UK" style="color: black;" /></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;">[http://www.youtube.com/watch?v=Dvagp3IRNSo <span style="color: black;">http://www.youtube.com/watch?v=Dvagp3IRNSo</span>]</span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;">[http://moyaskola.com.ua/index.php?option=com_content&view=article&id=53:2010-10-03-08-09-01&catid=6:7-&Itemid=3 <span style="color: black;">http://moyaskola.com.ua/index.php?option=com_content&view=article&id=53:2010-10-03-08-09-01&catid=6:7-&Itemid=3</span>]</span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;"><span style="text-decoration: none;"> </span></span></u>'''
| + | |
| - | | + | |
| - | '''<u><span lang="UK" style="color: black;">Список використаної літератури:</span></u>'''
| + | |
| - | | + | |
| - | <span lang="UK" style="color: black;">1. Урок на тему «Тотожні
| + | |
| - | вирази» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ
| + | |
| - | №323).</span>
| + | |
| - | | + | |
| - | <span lang="UK" style="color: black;">2. Урок на тему
| + | |
| - | «Перетворення тотожних виразів» викладача Конченко Т. М. , Гімназії міжнародних
| + | |
| - | відносин, м. Київ (СЗШ №323).</span>
| + | |
| - | | + | |
| - | <span lang="UK" style="color: black;">3. Істер О. А. «Алгебра. 7
| + | |
| - | клас».</span>
| + | |
| - | | + | |
| - | <span lang="UK" style="color: black;">4. Мерзляк А. Г., Полонський
| + | |
| - | В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного
| + | |
| - | оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.</span>
| + | |
| - | | + | |
| - | <span lang="UK" style="color: black;"> </span>
| + | |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <br>
| + | ---- |
| - | | + | |
| - | <br> <br> Відредаговано і надіслано Мазуренко М.С.<br>
| + | |
| - | | + | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | <br> Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ Образовательном форуме], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ блог''','''] Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ Гильдия Лидеров Образования] открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.<br> |
| | | | |
| | [[Category:Математика_7_клас]] | | [[Category:Математика_7_клас]] |
1. Степінь натурального числа з натуральним показником
2. Степінь дійсного числа з натуральним показником
3. Властивості степеня дійсного числа з натуральним показником
4. Степінь дійсного числа з нульовим і цілим від'ємним показником.
Поняття степеня натурального числа з натуральним показником узагальнюється на степінь дійсного числа з натуральним показником:
Парний степінь від'ємного числа – число додатне.
Непарний степінь від'ємного числа – число від'ємне.
Розв'язання. Якщо а= -2, то значення даного виразу дорівнює
При множенні степенів з однаковою основою показники степенів додають, а основу залишають ту ж саму.
Приклади. 32•38=310;
Щоб піднести степінь до степеня, потрібно показники степенів перемножити, а основу залишити ту саму.
Приклади. (32)8=316;
Цю формулу часто застосовують в зворотньому порядку.
Приклади.
Конченко Т. М.
Мазуренко М.С.