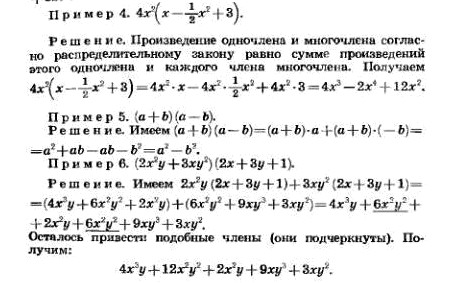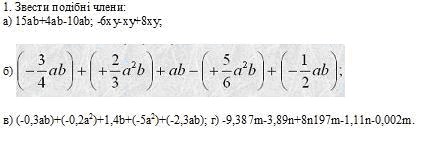|
|
|
| (4 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| | <metakeywords>Гіпермаркет Знань - перший в світі!, Гіпермаркет Знань, Математика, 7 клас, Тема 10, Многочлени</metakeywords> | | <metakeywords>Гіпермаркет Знань - перший в світі!, Гіпермаркет Знань, Математика, 7 клас, Тема 10, Многочлени</metakeywords> |
| | | | |
| - | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 7 клас. Повні уроки|Математика 7 клас. Повні уроки]]>> Алгебра: Многочлени''' | + | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 7 клас. Повні уроки|Математика 7 клас. Повні уроки]]>> Алгебра: Многочлени'''<br> |
| | | | |
| - | == Тема == | + | ==Тема== |
| | + | *'''Многочлени''' |
| | | | |
| - | *'''Многочлени'''<br>
| + | ==Мета== |
| - | | + | |
| - | == Мета == | + | |
| | | | |
| | *дізнатися, що таке многочлен. | | *дізнатися, що таке многочлен. |
| | | | |
| - | == План == | + | ==План== |
| | | | |
| | 1. Визначення многочлена | | 1. Визначення многочлена |
| Строка 17: |
Строка 16: |
| | 2. Приклади зведення многочленів | | 2. Приклади зведення многочленів |
| | | | |
| - | === Визначення многочлена === | + | ===Визначення многочлена=== |
| | | | |
| - | '''Суму кількох одночленів називають многочленом.''' Кожен доданок многочлена – його член.
| + | Суму кількох одночленів називають многочленом. Кожен доданок многочлена – його член. |
| | | | |
| - | Наприклад, '''[[Многочлени|многочлен]]''' 3ху+2х+у - містить три члени 3ху, 2х і у. | + | Наприклад, [[Многочлени|многочлен]] 3ху+2х+у - містить три члени 3ху, 2х і у. |
| | | | |
| - | '''[[Фішки до уроку «Розкладання многочленів на множники різними способами. Перетворення виразів»|Многочлен]]''', який містить два чи три доданки, називається відповідно '''двочленом, або тричленом. '''
| + | [[Фішки до уроку «Розкладання многочленів на множники різними способами. Перетворення виразів»|Многочлен]], який містить два чи три доданки, називається відповіднодвочленом, або тричленом. |
| | | | |
| - | '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів. Повні уроки|Одночлен]]''' є окремим видом многочленна. <br><br>Подібні члени многочлена – це такі доданки, які відрізняються лише коефіцієнтами, або зовсім не відрізняються. <br><br>Многочлен, який є сумою одночленів стандартного вигляду, серед яких немає подібних членів, називають '''многочленом стандартного вигляду.'''
| + | [[Одночлен. Піднесення одночленів до степеня. Множення одночленів. Повні уроки|Одночлен]] є окремим видом многочленна. <br><br>Подібні члени многочлена – це такі доданки, які відрізняються лише коефіцієнтами, або зовсім не відрізняються. <br><br>Многочлен, який є сумою одночленів стандартного вигляду, серед яких немає подібних членів, називають многочленом стандартного вигляду. |
| | | | |
| - | '''2a<sup>2</sup> + 3аb - 4 - многочлен стандартного вигляду.'''<br>'''<br>4аb - 5ас + 2а<sup>2</sup> - 3ас + а<sup>2</sup> - звичайний многочлен'''
| + | 2a<sup>2</sup> + 3аb - 4 - многочлен стандартного вигляду.<br>'''<br>'''4аb - 5ас + 2а<sup>2</sup> - 3ас + а<sup>2</sup> - звичайний многочлен <br> |
| - | <br> | + | |
| | | | |
| - | '''[[Степінь з натуральним показником. Властивості степеня. Повні уроки|Степенем]] многочлена''' стандартного вигляду називається найбільший '''[[Вирази зі степенями. Вправи та задачі|степінь]]''' одночлена, яких входить в цей многочлен. Наприклад, 4х<sup>3</sup>у<sup>3</sup> – многочлен шостого степеня. <br><br>'''Коренем многочлена '''називається таке значення змінної, при якому многочлен перетворюється в нуль.<br><br><br>http://rutube.ru/tracks/3064015.html?v=6c70e7bbbfef6755c834f0d44b9ce5cf<br><br>
| + | [[Степінь з натуральним показником. Властивості степеня. Повні уроки|Степенеммногочлена]] стандартного вигляду називається найбільший [[Вирази зі степенями. Вправи та задачі|степінь]] одночлена, яких входить в цей многочлен. Наприклад, 4х<sup>3</sup>у<sup>3</sup> – многочлен шостого степеня. <br><br>Коренем многочленаназивається таке значення змінної, при якому многочлен перетворюється в нуль.<br> |
| | | | |
| - | === Приклади зведення многочленів === | + | ===Приклади зведення многочленів=== |
| | | | |
| - | <br>Розглянемо приклади.<br>
| + | Приклад 1'''.''' 3a 5b+3ab+2a(-4b)+b b. |
| | | | |
| - | '''''Приклад 1.''''' 3a 5b+3ab+2a(-4b)+b b. | + | Розв'язок. Спочатку приведемо до стандартного вигляду члени многочлена. Отримаємо 15ab+3ab-8ab+b<sup>2</sup>. Після приведення подібних членів отримаємо многочлен стандартного вигляду 10ab+b<sup>2</sup>. |
| | | | |
| - | ''Розв'язок.'' Спочатку приведемо до стандартного вигляду члени многочлена. Отримаємо 15ab+3ab-8ab+b<sup>2</sup>. Після приведення подібних членів отримаємо многочлен стандартного вигляду 10ab+b<sup>2</sup>.
| + | Приклад 2. (3a+5b-2c)+(2a-b+4c).<br> |
| | | | |
| - | '''''Приклад 2.''''' (3a+5b-2c)+(2a-b+4c).<br>
| + | Розв'язок. Якщо перед дужками стоєть знак "плюс", то дужки можно опустити, зберігши знаки всіх додатків в дужках. Використавши це правило розкриття дужок, отримаємо: |
| - | | + | |
| - | ''Розв'язок.'' Якщо перед дужками стоєть знак "плюс", то дужки можно опустити, зберігши знаки всіх додатків в дужках. Використавши це правило розкриття дужок, отримаємо:
| + | |
| | | | |
| | 3a+5b-2c+2a-b+4c | | 3a+5b-2c+2a-b+4c |
| Строка 50: |
Строка 46: |
| | (3a+2a)+(5b-b)+(-2c+4c)=5a+4b+2c. | | (3a+2a)+(5b-b)+(-2c+4c)=5a+4b+2c. |
| | | | |
| - | '''''Приклад 3.''''' (5a<sup>2</sup>b+ab<sup>2</sup>)-(3a<sup>2</sup>b-4ab<sup>2</sup>) | + | Приклад 3'''.''' (5a<sup>2</sup>b+ab<sup>2</sup>)-(3a<sup>2</sup>b-4ab<sup>2</sup>) |
| | | | |
| - | ''Розв'язок.'' Якщо перед дужками стоєть знак "мінус", то дужки можно опустити, змінивши знаки всіх додатків в дужках. Використавши це правило розкриття дужок, отримаємо:
| + | Розв'язок. Якщо перед дужками стоєть знак "мінус", то дужки можно опустити, змінивши знаки всіх додатків в дужках. Використавши це правило розкриття дужок, отримаємо: |
| | | | |
| | 5a<sup>2</sup>b+ab<sup>2</sup>-3a<sup>2</sup>b+4ab<sup>2</sup>=<sup></sup>(5a<sup>2</sup>b-3a<sup>2</sup>b)+(ab<sup>2</sup>+4ab<sup>2</sup>)=2a<sup>2</sup>b+5ab<sup>2</sup> | | 5a<sup>2</sup>b+ab<sup>2</sup>-3a<sup>2</sup>b+4ab<sup>2</sup>=<sup></sup>(5a<sup>2</sup>b-3a<sup>2</sup>b)+(ab<sup>2</sup>+4ab<sup>2</sup>)=2a<sup>2</sup>b+5ab<sup>2</sup> |
| Строка 60: |
Строка 56: |
| | [[Image:1901-76.jpg|480px|Приклад 4]] | | [[Image:1901-76.jpg|480px|Приклад 4]] |
| | | | |
| - | === Перевір себе === | + | ===Перевір себе=== |
| | | | |
| | <br>[[Image:1901-4.jpg|480px|Завдання]] | | <br>[[Image:1901-4.jpg|480px|Завдання]] |
| Строка 68: |
Строка 64: |
| | [[Image:1901-5.jpg|480px|Завдання]] | | [[Image:1901-5.jpg|480px|Завдання]] |
| | | | |
| - | <br>3. <br> <br>[[Image:1901-6.jpg|480px|Завдання]] | + | <br>3. <br> <br>[[Image:1901-6.jpg|480px|Завдання]]<br> |
| - | | + | |
| - | <br> | + | |
| | | | |
| - | == Список використаної літератури == | + | ==Список використаної літератури== |
| | | | |
| - | <br>''1. Урок на тему «Многочлени» викладача Конченко Т. М. , '''[http://xvatit.com/vuzi/ Гімназії міжнародних відносин]''', м. Київ (СЗШ №323).<br>2. Істер О. А. «Алгебра. 7 клас».<br>3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.''<br> | + | <br>''1. Урок на тему «Многочлени» викладача Конченко Т. М. , '[http://xvatit.com/vuzi/ Гімназії міжнародних відносин]', м. Київ (СЗШ №323).<br>2. Істер О. А. Алгебра. [[7_клас_уроки|7 клас]].<br>3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.''<br> |
| | | | |
| | ---- | | ---- |
| Строка 92: |
Строка 86: |
| | ---- | | ---- |
| | | | |
| - | <br> Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ '''Образовательном форуме'''], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ '''блог,'''] Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ '''Гильдия Лидеров Образования'''] открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.<br> | + | <br> Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ Образовательном форуме], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ блог,] Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ Гильдия Лидеров Образования] открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.<br> |
| | | | |
| | [[Category:Математика_7_клас]] | | [[Category:Математика_7_клас]] |
Текущая версия на 12:32, 25 декабря 2012
Гіпермаркет Знань>>Математика>>Математика 7 клас. Повні уроки>> Алгебра: Многочлени
Тема
Мета
- дізнатися, що таке многочлен.
План
1. Визначення многочлена
2. Приклади зведення многочленів
Визначення многочлена
Суму кількох одночленів називають многочленом. Кожен доданок многочлена – його член.
Наприклад, многочлен 3ху+2х+у - містить три члени 3ху, 2х і у.
Многочлен, який містить два чи три доданки, називається відповіднодвочленом, або тричленом.
Одночлен є окремим видом многочленна.
Подібні члени многочлена – це такі доданки, які відрізняються лише коефіцієнтами, або зовсім не відрізняються.
Многочлен, який є сумою одночленів стандартного вигляду, серед яких немає подібних членів, називають многочленом стандартного вигляду.
2a2 + 3аb - 4 - многочлен стандартного вигляду.
4аb - 5ас + 2а2 - 3ас + а2 - звичайний многочлен
Степенеммногочлена стандартного вигляду називається найбільший степінь одночлена, яких входить в цей многочлен. Наприклад, 4х3у3 – многочлен шостого степеня.
Коренем многочленаназивається таке значення змінної, при якому многочлен перетворюється в нуль.
Приклади зведення многочленів
Приклад 1. 3a 5b+3ab+2a(-4b)+b b.
Розв'язок. Спочатку приведемо до стандартного вигляду члени многочлена. Отримаємо 15ab+3ab-8ab+b2. Після приведення подібних членів отримаємо многочлен стандартного вигляду 10ab+b2.
Приклад 2. (3a+5b-2c)+(2a-b+4c).
Розв'язок. Якщо перед дужками стоєть знак "плюс", то дужки можно опустити, зберігши знаки всіх додатків в дужках. Використавши це правило розкриття дужок, отримаємо:
3a+5b-2c+2a-b+4c
і далі
(3a+2a)+(5b-b)+(-2c+4c)=5a+4b+2c.
Приклад 3. (5a2b+ab2)-(3a2b-4ab2)
Розв'язок. Якщо перед дужками стоєть знак "мінус", то дужки можно опустити, змінивши знаки всіх додатків в дужках. Використавши це правило розкриття дужок, отримаємо:
5a2b+ab2-3a2b+4ab2=(5a2b-3a2b)+(ab2+4ab2)=2a2b+5ab2
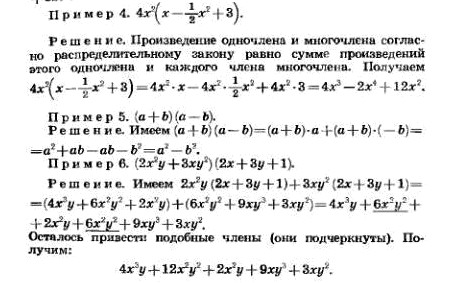
Перевір себе
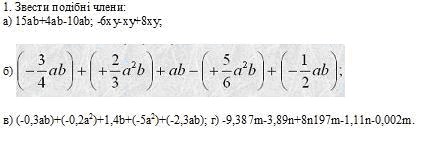

3.

Список використаної літератури
1. Урок на тему «Многочлени» викладача Конченко Т. М. , 'Гімназії міжнародних відносин', м. Київ (СЗШ №323).
2. Істер О. А. Алгебра. 7 клас.
3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.
Відредаговано і надіслано Мазуренко М.С.
Над уроком працювали
Конченко Т. М.
Мазуренко М.С.
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
Предмети > Математика > Математика 7 клас
|