|
|
| (3 промежуточные версии не показаны) |
| Строка 1: |
Строка 1: |
| | <metakeywords>Гіпермаркет Знань - перший в світі!, Гіпермаркет Знань, Математика, 7 клас, Тема 27, Система лінійних рівнянь з двома змінними</metakeywords> | | <metakeywords>Гіпермаркет Знань - перший в світі!, Гіпермаркет Знань, Математика, 7 клас, Тема 27, Система лінійних рівнянь з двома змінними</metakeywords> |
| | | | |
| - | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 7 клас. Повні уроки|Математика 7 клас. Повні уроки]]>> АЛГЕБРА: Система лінійних рівнянь з двома змінними''' | + | '''[[Гіпермаркет Знань - перший в світі!|Гіпермаркет Знань]]>>[[Математика|Математика]]>>[[Математика 7 клас. Повні уроки|Математика 7 клас. Повні уроки]]>> Алгебра: Система лінійних рівнянь з двома змінними''' |
| | | | |
| - | <br> '''АЛГЕБРА'''<br>
| + | ==Тема== |
| | + | *'''Система лінійних рівнянь з двома змінними''' |
| | | | |
| - | <br>
| + | ==Мета== |
| - | | + | |
| - | == <u>'''Тема уроку'''</u> == | + | |
| - | | + | |
| - | *<u>'''Система лінійних рівнянь з двома змінними'''</u>
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | == <u>'''Мета уроку'''</u> ==
| + | |
| | | | |
| | *зрозуміти, що таке системи рівнянь; навчитися розв’язувати задачі та цю тему.<br> | | *зрозуміти, що таке системи рівнянь; навчитися розв’язувати задачі та цю тему.<br> |
| | | | |
| - | <br>
| + | ==План== |
| - | | + | |
| - | == <u>'''Хід уроку'''</u> == | + | |
| - | | + | |
| - | <br>
| + | |
| | | | |
| - | === Визначення системи рівнянь === | + | ===Визначення системи рівнянь === |
| | | | |
| - | '''Системою рівнянь''' називаються два або декілька рівнянь, у яких потрібно знайти всі спільні розв'язки. Приклад:
| + | [[Система лінійних рівнянь з двома змінними|Системою рівнянь]] називаються два або декілька рівнянь, у яких потрібно знайти всі спільні розв'язки. Приклад: |
| | | | |
| | [[Image:20-03-10-01.jpg]]2x-3y=9, 3х+2у=7. | | [[Image:20-03-10-01.jpg]]2x-3y=9, 3х+2у=7. |
| | | | |
| - | Рівняння системи записуються стовпчиком і об’єднуються фігурною дужкою. Розв'язками такої системи є множина упорядкованих пар чисел (х; у). | + | [[Рівняння. Корені рівняння. Розв'язування рівнянь. Повні уроки|Рівняння]] системи записуються стовпчиком і об’єднуються фігурною дужкою. Розв'язками такої системи є множина упорядкованих пар чисел (х; у). |
| | | | |
| - | Система рівнянь називається '''лінійною''', якщо всі рівняння, що входять до системи, є лінійними. Приклад: пара чисел (3; -1) є розв'язком системи: <br> | + | Система рівнянь називається лінійною, якщо всі рівняння, що входять до системи, є лінійними. Приклад: пара чисел (3; -1) є розв'язком системи: <br> |
| | | | |
| | [[Image:20-03-10-01.jpg]]2x-3y=9, 3х+2у=7. | | [[Image:20-03-10-01.jpg]]2x-3y=9, 3х+2у=7. |
| | | | |
| - | Систему двох лінійних рівнянь з двома змінними записують у такому вигляді:<br> | + | Систему двох [[Лінійне рівняння з однією змінною. Повні уроки|лінійних рівнянь]] з двома змінними записують у такому вигляді:<br> |
| | | | |
| - | [[Image:20-03-10-01.jpg]]а<sub>1</sub>+b<sub>1</sub>y=c<sub>1</sub> ; a<sub>2</sub>+b<sub>2</sub>y=c<sub>2</sub> | + | [[Image:20-03-10-01.jpg]]а<sub>1</sub>+b<sub>1</sub>y=c<sub>1</sub> ; a<sub>2</sub>+b<sub>2</sub>y=c<sub>2</sub> |
| | | | |
| - | === Розв'язок системи рівнянь === | + | ===Розв'язок системи рівнянь=== |
| | | | |
| - | '''Розв'язати систему рівнянь''' – означає знайти всі її розв'язки або довести, що розв’язків немає. | + | [[Розв'язування задач, рівняннь|Розв'язати систему рівнянь]] – означає знайти всі її розв'язки або довести, що розв’язків немає. |
| | | | |
| - | Якщо система має скінченне число розв’язків, то вона називається '''визначеною.''' | + | Якщо система має скінченне число розв’язків, то вона називається визначеною. |
| | | | |
| - | Якщо система має нескінченну множину розв’язків, то система називається '''невизначеною'''. | + | Якщо система має нескінченну множину розв’язків, то система називається невизначеною. |
| | | | |
| - | Дві системи називаються'''рівносильними''', якщо вони мають однакову множину розв’язків. | + | Дві системи називаються [[Рівносильні рівняння. Основні властивості рівнянь. Повні уроки|рівносильними]], якщо вони мають однакову множину розв’язків. |
| | | | |
| | Якщо система із n лінійних рівнянь містить n невідомих, то можливі такі три випадки: | | Якщо система із n лінійних рівнянь містить n невідомих, то можливі такі три випадки: |
| Строка 59: |
Строка 46: |
| | - Система має нескінченно багато розв’язків. | | - Система має нескінченно багато розв’язків. |
| | | | |
| | + | <br> |
| | | | |
| | + | Система <br> |
| | | | |
| - | Система <br>
| + | [[Image:20-03-10-01.jpg]]а<sub>1</sub>+b<sub>1</sub>y=c<sub>1</sub> ; a<sub>2</sub>+b<sub>2</sub>y=c<sub>2</sub> |
| - | | + | |
| - | [[Image:20-03-10-01.jpg]]а<sub>1</sub>+b<sub>1</sub>y=c<sub>1</sub> ; a<sub>2</sub>+b<sub>2</sub>y=c<sub>2</sub> | + | |
| | | | |
| - | Не має розв'язків, якщо [[Image:20-03-10-02.jpg]] | + | Не має розв'язків, якщо [[Image:20-03-10-02.jpg|Розв'язок]] |
| | | | |
| - | Має єдиний розв'язок, якщо [[Image:20-03-10-03.jpg]] | + | Має єдиний розв'язок, якщо [[Image:20-03-10-03.jpg|Розв'язок]] |
| | | | |
| - | Має нескінченне число розв'язків, якщо [[Image:20-03-10-04.jpg]] | + | Має нескінченне число розв'язків, якщо [[Image:20-03-10-04.jpg|Розв'язок]] |
| | | | |
| - | Приклад: <br> | + | Приклад: <br> |
| | | | |
| | 1. [[Image:20-03-10-01.jpg]]3x-4y=15, 6х-8у=11. | | 1. [[Image:20-03-10-01.jpg]]3x-4y=15, 6х-8у=11. |
| | | | |
| - | [[Image:20-03-10-05.jpg]] – розв'язків немає. <br> | + | [[Image:20-03-10-05.jpg|Розв'язок]] – розв'язків немає. <br> |
| | | | |
| | 2. [[Image:20-03-10-01.jpg]]3x-4y=13, х+у=9. | | 2. [[Image:20-03-10-01.jpg]]3x-4y=13, х+у=9. |
| | | | |
| - | [[Image:20-03-10-06-1.jpg]] – єдиний розв'язок (7; 2); <br> | + | [[Image:20-03-10-06-1.jpg|Розв'язок]] – єдиний розв'язок (7; 2); <br> |
| | | | |
| | 3. [[Image:20-03-10-01.jpg]]3x-4y=15, 6х-8у=30. | | 3. [[Image:20-03-10-01.jpg]]3x-4y=15, 6х-8у=30. |
| | | | |
| - | [[Image:20-03-10-07.jpg]] – нескінченно багато розв'язків. | + | [[Image:20-03-10-07.jpg|Розв'язок]] – нескінченно багато розв'язків. |
| | | | |
| | <br> | | <br> |
| Строка 89: |
Строка 76: |
| | {{#ev:youtube| hdbJCKGlVh4}} | | {{#ev:youtube| hdbJCKGlVh4}} |
| | | | |
| - | == '''Корисна інформація''' == | + | ===Корисна інформація=== |
| | | | |
| - | <br> <br>[[Image:1901-68.jpg|687x445px|1901-68.jpg]] | + | <br> <br>[[Image:1901-68.jpg|480px|Таблиця]] |
| | | | |
| | <br> | | <br> |
| | | | |
| - | '''Приклад 1.''' Скільки розв'язків має система рівнянь <br>
| + | Приклад 1. Скільки розв'язків має система рівнянь <br> |
| | | | |
| | [[Image:20-03-10-01.jpg]]-2x+y=2, -6х+3у=6? | | [[Image:20-03-10-01.jpg]]-2x+y=2, -6х+3у=6? |
| | | | |
| - | *Побудуємо графік рівнянь системи. | + | *Побудуємо [[Графік лінійного рівняння з двома змінними|графік рівнянь]] системи. |
| | | | |
| | {| width="200" cellspacing="1" cellpadding="1" border="1" | | {| width="200" cellspacing="1" cellpadding="1" border="1" |
| Строка 105: |
Строка 92: |
| | | colspan="3" | -2x+y=2 | | | colspan="3" | -2x+y=2 |
| | |- | | |- |
| - | | х<br> | + | | х<br> |
| - | | 0<br> | + | | 0<br> |
| | | -1<br> | | | -1<br> |
| | |- | | |- |
| - | | у<br> | + | | у<br> |
| - | | 2<br> | + | | 2<br> |
| | | 0<br> | | | 0<br> |
| | |} | | |} |
| | | | |
| - | | + | <br> |
| | | | |
| | {| width="200" cellspacing="1" cellpadding="1" border="1" | | {| width="200" cellspacing="1" cellpadding="1" border="1" |
| Строка 120: |
Строка 107: |
| | | colspan="3" | -6х+3у=6 | | | colspan="3" | -6х+3у=6 |
| | |- | | |- |
| - | | х<br> | + | | х<br> |
| - | | 0<br> | + | | 0<br> |
| | | -1<br> | | | -1<br> |
| | |- | | |- |
| - | | у<br> | + | | у<br> |
| - | | 2<br> | + | | 2<br> |
| | | 0<br> | | | 0<br> |
| | |} | | |} |
| | | | |
| - | <br> | + | <br> |
| | | | |
| - | [[Image:20-03-10-08.jpg]] <br> | + | [[Image:20-03-10-08.jpg|240px|Графік]] <br> |
| | | | |
| | Графіки співпадають. Система рівнянь має безліч розв'язків. | | Графіки співпадають. Система рівнянь має безліч розв'язків. |
| | | | |
| - | '''Приклад 2. '''Скільки розв'язків має система рівнянь <br>
| + | Приклад 2. Скільки розв'язків має система рівнянь <br> |
| | | | |
| | [[Image:20-03-10-01.jpg]]x+y=3, 2х+2у=3? | | [[Image:20-03-10-01.jpg]]x+y=3, 2х+2у=3? |
| Строка 145: |
Строка 132: |
| | | colspan="3" | x+y=3 | | | colspan="3" | x+y=3 |
| | |- | | |- |
| - | | х<br> | + | | х<br> |
| - | | 0<br> | + | | 0<br> |
| | | 3<br> | | | 3<br> |
| | |- | | |- |
| - | | у<br> | + | | у<br> |
| - | | 3<br> | + | | 3<br> |
| | | 0<br> | | | 0<br> |
| | |} | | |} |
| | | | |
| - | | + | <br> |
| | | | |
| | {| width="200" cellspacing="1" cellpadding="1" border="1" | | {| width="200" cellspacing="1" cellpadding="1" border="1" |
| Строка 160: |
Строка 147: |
| | | colspan="3" | 2х+2у=3 | | | colspan="3" | 2х+2у=3 |
| | |- | | |- |
| - | | х<br> | + | | х<br> |
| - | | 0<br> | + | | 0<br> |
| | | 1,5<br> | | | 1,5<br> |
| | |- | | |- |
| - | | у<br> | + | | у<br> |
| - | | 1,5<br> | + | | 1,5<br> |
| | | 0<br> | | | 0<br> |
| | |} | | |} |
| | | | |
| - | <br> | + | <br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| - | [[Image:20-03-10-09.jpg]] <br> | + | [[Image:20-03-10-09.jpg|240px|Графік]] <br> |
| | | | |
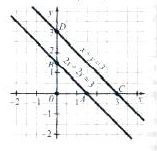
| | Графіками рівнянь є паралельні прямі (бо <OAB=<OCD=45<sup>0</sup>). Система рівнянь розв'язків немає. | | Графіками рівнянь є паралельні прямі (бо <OAB=<OCD=45<sup>0</sup>). Система рівнянь розв'язків немає. |
| | | | |
| - | <br><br><br> <br>
| + | <br> |
| | | | |
| - | == <u>'''Самостійна робота'''</u> == | + | ===Самостійна робота=== |
| | | | |
| - | 1. Складіть які-небудь систему рівнянь, що має розв'язків х=-2; у=1. 2. Складіть яку-небудь систему рівнянь, що має розв'язок (3;-1). 3. Скіль3ки розв'язків має система рівнянь: <br> | + | 1. Складіть які-небудь систему рівнянь, що має розв'язків х=-2; у=1. 2. Складіть яку-небудь систему рівнянь, що має розв'язок (3;-1). 3. Скіль3ки розв'язків має система рівнянь: <br> |
| | | | |
| - | а). [[Image:20-03-10-01.jpg]]х-2у=-3; 2х-4у=-6. <br> | + | а). [[Image:20-03-10-01.jpg]]х-2у=-3; 2х-4у=-6. <br> |
| | | | |
| - | б). [[Image:20-03-10-01.jpg]]3х-у=2; 6х-2у=-3. <br> | + | б). [[Image:20-03-10-01.jpg]]3х-у=2; 6х-2у=-3. <br> |
| | | | |
| - | в). [[Image:20-03-10-01.jpg]]х+3у=4; 4х+у=-5. <br> | + | в). [[Image:20-03-10-01.jpg]]х+3у=4; 4х+у=-5. <br> |
| | | | |
| - | г). [[Image:20-03-10-01.jpg]]у=2х-4; 4х-2у=8. <br> | + | г). [[Image:20-03-10-01.jpg]]у=2х-4; 4х-2у=8. <br> |
| | | | |
| - | д). [[Image:20-03-10-01.jpg]]х+3у=-2; 2х+6у=-4. <br> | + | д). [[Image:20-03-10-01.jpg]]х+3у=-2; 2х+6у=-4. <br> |
| | | | |
| - | е). [[Image:20-03-10-01.jpg]]3х-2у=1; 9х-6у=-2. <br> | + | е). [[Image:20-03-10-01.jpg]]3х-2у=1; 9х-6у=-2. <br> |
| | | | |
| | ж). [[Image:20-03-10-01.jpg]]х-2у=-2; х+4у=0. | | ж). [[Image:20-03-10-01.jpg]]х-2у=-2; х+4у=0. |
| Строка 215: |
Строка 202: |
| | <br> | | <br> |
| | | | |
| | + | ==Список використаної літератури== |
| | + | |
| | + | ''1. Урок на тему «Система лінійних рівнянь з двома змінними» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323). <br> 2. Істер О. А. «Алгебра. [[7_клас_уроки|7 клас]]». <br>3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачі завдань для тематичного оцінювання з алгебри для 7 класу. – Харків, [http://xvatit.com/vuzi/ Гімназія], 2004. – 112 с.: іл. '' |
| | <br> | | <br> |
| | | | |
| - | == <u>Список використаної літератури</u> ==
| + | ---- |
| | | | |
| - | *1. Урок на тему «Система лінійних рівнянь з двома змінними» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).
| + | <br> ''Відредаговано і надіслано Мазуренко М.С.''<br> |
| - | *2. Істер О. А. «Алгебра. 7 клас».
| + | |
| - | *3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачі завдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.
| + | |
| - | | + | |
| - | <br> <br> Відредаговано і надіслано Мазуренко М.С.<br>
| + | |
| | | | |
| | ---- | | ---- |
| | | | |
| - | '''<u>Над уроком працювали</u>''' | + | '''Над уроком працювали''' |
| | | | |
| - | <!--[if gte mso 9]><xml>
| + | Борда Ю.Д. |
| - | <w:WordDocument>
| + | |
| - | <w:View>Normal</w:View>
| + | |
| - | <w:Zoom>0</w:Zoom>
| + | |
| - | <w:PunctuationKerning/>
| + | |
| - | <w:ValidateAgainstSchemas/>
| + | |
| - | <w:SaveIfXMLInvalid>false</w:SaveIfXMLInvalid>
| + | |
| - | <w:IgnoreMixedContent>false</w:IgnoreMixedContent>
| + | |
| - | <w:AlwaysShowPlaceholderText>false</w:AlwaysShowPlaceholderText>
| + | |
| - | <w:Compatibility>
| + | |
| - | <w:BreakWrappedTables/>
| + | |
| - | <w:SnapToGridInCell/>
| + | |
| - | <w:WrapTextWithPunct/>
| + | |
| - | <w:UseAsianBreakRules/>
| + | |
| - | <w:DontGrowAutofit/>
| + | |
| - | </w:Compatibility>
| + | |
| - | <w:BrowserLevel>MicrosoftInternetExplorer4</w:BrowserLevel>
| + | |
| - | </w:WordDocument>
| + | |
| - | </xml><![endif]--><!--[if gte mso 9]><xml>
| + | |
| - | <w:LatentStyles DefLockedState="false" LatentStyleCount="156">
| + | |
| - | </w:LatentStyles>
| + | |
| - | </xml><![endif]--><!--[if gte mso 10]>
| + | |
| - | <style>
| + | |
| - | /* Style Definitions */
| + | |
| - | table.MsoNormalTable
| + | |
| - | {mso-style-name:"Обычная таблица";
| + | |
| - | mso-tstyle-rowband-size:0;
| + | |
| - | mso-tstyle-colband-size:0;
| + | |
| - | mso-style-noshow:yes;
| + | |
| - | mso-style-parent:"";
| + | |
| - | mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
| + | |
| - | mso-para-margin:0cm;
| + | |
| - | mso-para-margin-bottom:.0001pt;
| + | |
| - | mso-pagination:widow-orphan;
| + | |
| - | font-size:10.0pt;
| + | |
| - | font-family:"Times New Roman";
| + | |
| - | mso-ansi-language:#0400;
| + | |
| - | mso-fareast-language:#0400;
| + | |
| - | mso-bidi-language:#0400;}
| + | |
| - | </style>
| + | |
| - | <![endif]--><span lang="UK" style="font-size: 14pt; font-family: Arial;">
| + | |
| - | </span>
| + | |
| - | | + | |
| - | <br> Борда Ю.Д.
| + | |
| | | | |
| | Конченко Т. М. | | Конченко Т. М. |
| | | | |
| | Мазуренко М.С. | | Мазуренко М.С. |
| - |
| |
| - | ----
| |
| | | | |
| | <br> | | <br> |
| | | | |
| - | Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ '''Образовательном форуме'''], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ '''блог,'''] Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ '''Гильдия Лидеров Образования'''] открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.<br> | + | ---- |
| | + | |
| | + | <br> Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ Образовательном форуме], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ блог''','''] Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ Гильдия Лидеров Образования] открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.<br> |
| | | | |
| | [[Category:Математика_7_клас]] | | [[Category:Математика_7_клас]] |
Система рівнянь називається лінійною, якщо всі рівняння, що входять до системи, є лінійними. Приклад: пара чисел (3; -1) є розв'язком системи:
Якщо система має скінченне число розв’язків, то вона називається визначеною.
Якщо система має нескінченну множину розв’язків, то система називається невизначеною.
Якщо система із n лінійних рівнянь містить n невідомих, то можливі такі три випадки:
- Система має нескінченно багато розв’язків.
1. 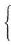 3x-4y=15, 6х-8у=11.
3x-4y=15, 6х-8у=11.
2. 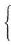 3x-4y=13, х+у=9.
3x-4y=13, х+у=9.
3. 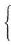 3x-4y=15, 6х-8у=30.
3x-4y=15, 6х-8у=30.
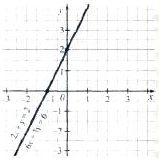
Приклад 1. Скільки розв'язків має система рівнянь
Графіки співпадають. Система рівнянь має безліч розв'язків.
Приклад 2. Скільки розв'язків має система рівнянь
1. Складіть які-небудь систему рівнянь, що має розв'язків х=-2; у=1. 2. Складіть яку-небудь систему рівнянь, що має розв'язок (3;-1). 3. Скіль3ки розв'язків має система рівнянь:
а). 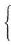 х-2у=-3; 2х-4у=-6.
х-2у=-3; 2х-4у=-6.
б). 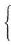 3х-у=2; 6х-2у=-3.
3х-у=2; 6х-2у=-3.
в). 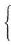 х+3у=4; 4х+у=-5.
х+3у=4; 4х+у=-5.
г). 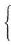 у=2х-4; 4х-2у=8.
у=2х-4; 4х-2у=8.
д). 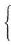 х+3у=-2; 2х+6у=-4.
х+3у=-2; 2х+6у=-4.
е). 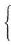 3х-2у=1; 9х-6у=-2.
3х-2у=1; 9х-6у=-2.
ж). 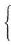 х-2у=-2; х+4у=0.
х-2у=-2; х+4у=0.
4. Знайдіть які-небудь два розв'язки системи рівнянь:
5. Для яких коефіцієнтів a та b пара чисел (2;-1) є розв'язком системи рівнянь:
6. Розв'яжіть графічно систему рівнянь:
a). 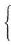 |x|-y=0; x-y=-2
|x|-y=0; x-y=-2
b). 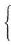 |2x|-y=0 y=3
|2x|-y=0 y=3
с). 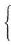 |x|-y=0 x-3y=-4.
|x|-y=0 x-3y=-4.
Борда Ю.Д.
Конченко Т. М.
Мазуренко М.С.