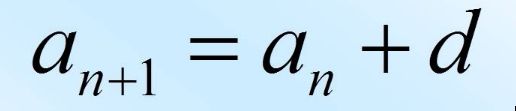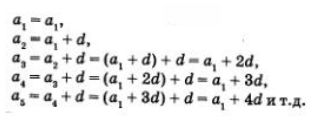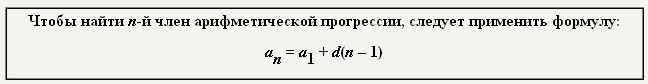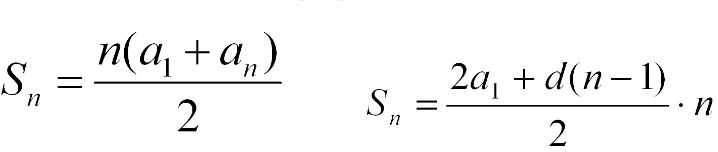|
|
|
| (9 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Арифметическая прогрессия<metakeywords>Арифметическая прогрессия</metakeywords>''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Арифметическая прогрессия<metakeywords>Арифметическая прогрессия, арифметической прогрессии, числовую последовательность, Формула n-го члена, натурального числа, линейную функцию, уравнения, математической модели, системой уравнений, трехзначных чисел, среднему арифметическому</metakeywords>''' |
| - | | + | |
| - | А.Г. Мордкович Алгебра 9 класс
| + | |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> | + | <h2> Определение арифметической прогрессии</h2> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | Арифметической прогрессией называют такую последовательность, в которой каждый член, начиная со второго, равняется предыдущему, к которому прибавляют одно и то же число. |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | Число d, которое в переводе обозначает слово «разница», носит название разницы арифметической прогрессии. |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | Иными словами можно сказать, что арифметическая прогрессия — это числовая последовательность (аn), заданная рекуррентно соотношениями |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| | + | <br> |
| | + | [[Image:9kl_ArProgressia01.jpg|500x500px|пифагор]] |
| | + | <br> |
| | + | |
| | + | При этом n = 2, 3, 4 |
| | + | |
| | + | Где, a и d являются заданными числами. |
| | + | |
| | + | То есть, такая числовая последовательность, как a1, a2, а3, ..., аn ... считается арифметической прогрессией. |
| | + | |
| | + | Иначе говоря, числовая последовательность a1, a2, а3, ..., а n ... является арифметической прогрессией, если для любого натурального числа n выполняется условие an + 1 = an + d. Из этого равенства следует равенство an + 1 - an = d которая означает, что разница между любым следующим и предыдущим членами арифметической прогрессии р. |
| | + | |
| | + | '''Например''' |
| | + | |
| | + | Если взять последовательность чисел 4; 12; 20; 25; 36, то мы увидим, что каждое последующее число на восемь больше предыдущего. Такая последовательность получается за счет прибавления числа восемь к каждому следующему члену. |
| | + | |
| | + | Вот такая получается арифметическая прогрессия: |
| | + | |
| | + | • 4+8=12<br> |
| | + | • 12+8=17<br> |
| | + | • 20+8=28<br> |
| | + | • 28+8=31<br> |
| | + | |
| | + | Для обозначения арифметической последовательности (аn), удобной является такая запись, как: |
| | + | |
| | + | + a1, a2, а3, ..., аn ... |
| | + | |
| | + | Здесь значок «+» служит заменой такого словосочетания, как «арифметическая прогрессия». |
| | + | |
| | + | '''Задание''' |
| | + | |
| | + | Перед вами предоставлена такая последовательность чисел: |
| | + | |
| | + | 3, 6, 9, 12, 15, 18,…… |
| | + | |
| | + | Дайте ответ на такие вопросы: |
| | + | |
| | + | 1. Можно ли назвать изображенный перечень чисел арифметической прогрессией?<br> |
| | + | 2. Назовите ее первый член.<br> |
| | + | 3. Чему равен ее десятый член?<br> |
| | + | 4. Найдите разность этой прогрессии.<br> |
| | + | 5. Какой будет сумма первых четырнадцати ее членов?<br> |
| | + | 6. К какой последовательности относится эта арифметическая прогрессия? К возрастающей или убывающей?<br> |
| | + | 7. Сделайте запись формулы ее n-го члена.<br> |
| | + | |
| | + | <h2> Формула арифметической прогрессии</h2> |
| | + | |
| | + | Такое нахождение арифметической прогрессии, в котором чтобы вычислить аn, необходимо еще найти и 99 предшествующих членов последовательности, является не совсем удобным. Естественно, что такую вычислительную работу буден лучше выполнить при помощи формулы n-го члена, то есть осуществить аналитическое задание арифметической прогрессии. |
| | + | |
| | + | Припустим, что первый член арифметической прогрессии равен а1, а d - разница. |
| | + | |
| | + | Тогда: |
| | + | |
| | + | <br> |
| | + | [[Image:9kl_ArProgressia02.jpg|300x300px|пифагор]] |
| | + | <br> |
| | | | |
| - | '''<u>Практика</u>'''
| + | Мы видим, что в этих формулах коэффициент при числе d на один меньше порядкового номера члена прогрессии. |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - |
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | <br> |
| | + | [[Image:9kl_ArProgressia03.jpg|600x400px|пифагор]] |
| | <br> | | <br> |
| | + | <br> |
| | + | [[Image:9kl_ArProgressia04.jpg|500x500px|пифагор]] |
| | + | <br> |
| | + | |
| | + | <h2> Формула суммы членов конечной арифметической прогрессии</h2> |
| | + | |
| | + | <br> |
| | + | [[Image:9kl_ArProgressia05.jpg|500x500px|пифагор]] |
| | + | <br> |
| | + | |
| | + | <h2> Характеристическое свойство арифметической прогрессии</h2> |
| | + | |
| | + | <br> |
| | + | [[Image:9kl_ArProgressia06.jpg|500x500px|пифагор]] |
| | + | <br> |
| | + | |
| | + | '''Задание''' |
| | + | |
| | + | Решите несколько бытовых задач: |
| | + | |
| | + | 1. По рекомендации санаторного врача, отдыхающим было рекомендовано начинать принимать загар с пяти минут, увеличивая ежедневно время пребывание на солнце, еще на пять минут. Сколько дней будет длиться путевка в санатории, если время загара увеличится до 30 минут?<br> |
| | + | |
| | + | 2. Спортсмен за час пробегает расстояние в 10 км. Каждый следующий час бега его расстояние уменьшается на 0,5 км, чем предыдущий. За сколько времени он пробежит 50 км?<br> |
| | + | |
| | + | 3. В театре сидячие места расположены так, что в каждом следующем ряду количество кресел на четыре больше, чем в предыдущем, а всего в зале насчитывается 1050 мест. Назовите количество рядов в зале, если первый ряд насчитывает десять кресел?<br> |
| | + | |
| | + | <h2> Историческая справка</h2> |
| | + | |
| | + | А известно ли вам, что создание формулы 1-х n – членов арифметической прогрессии тесно переплетается с именем такого ученого, как Карл Фридрих Гаусс. Будучи еще совсем ребенком, он проявлял себя истинным вундеркиндом, и кроме того, что умел читать и писать, умудрялся исправлять ошибки отца в подсчетах. |
| | + | |
| | + | Если верить легенде, то во время учебы, когда учитель предложил детям сосчитать сумму чисел от одного до ста, то восьмилетний Карл Гаусс очень быстро нашел искомую величину, так как смог заметить, что попарные суммы с противоположных сторон имеют одинаковый результат. Немного позднее он вывел формулу арифметической прогрессии. |
| | + | |
| | + | А вот «прогрессия», как термин появился в шестом веке благодаря римлянину Боэцию и воспринимался, как бесконечная числовая последовательность. И уже древние греки из теории непрерывных пропорций выделили такие названия, как «арифметическая» и «геометрическая» прогрессия. |
| | + | |
| | + | Задание: А вы сможете быстро подсчитать сумму от 1 до 100? Может среди нас тоже есть Гауссы-вундеркинды? |
| | + | |
| | + | <h2> Интересные факты</h2> |
| | + | |
| | + | В 1796 году Карл Фридрих Гаусс решил окончательно посвятить себя математике, потому что обнаружил метод, который позволил построить правильный семнадцатиугольник только с помощью линейки и циркуля! Над этой задачей бились все известные математики-геометры еще со времен великого Эвклида! А ведь изначально Гаусс собирался посвятить себя классической литературе, из-за необыкновенных склонностей к языкам. |
| | + | |
| | + | Некоторые факты, о математических прогрессиях были известны еще древним китайским и индийским мудрецам. Так, например, есть древняя индийская легенда, которая рассказывает об изобретении шахмат, а которой проходят моменты, связанные со знаниями арифметической прогрессии. |
| | + | |
| | + | Легенда рассказывает, как индийский шах Шерам пообещал награду тому, кто придумает интересную игр, которая вызовет длительный интерес у индийского владыки. Но мудрец Сета, который придумал шахматы, попросил за ее изобретение такое количество зерен, которое будет увеличиваться в зависимости от клеток на шахматной доске. И если на первую клеточку нужно положить только одно зернышко, то на следующую в два раза больше. И так каждый раз количество зерен на каждой следующей клетке снова удваивается по сравнению с предыдущей и т.д. вплоть до шестьдесят четвертой клетки. |
| | + | Это значит, что количество зерен равняется сумме шестидесяти четырех членной геометрической прогрессии. В итоге должно было получиться такое число зерен, которое нужно было бы собирать со всей планеты. Поэтому шах просьбу ученого выполнить никак не мог. |
| | + | |
| | + | А вот с помощью вычислений английский математик Абрахам де Муавр смог предсказать дату своей кончины. Наблюдая за продолжительностью своего сна, он заметил, что она с каждым днем увеличивается на пятнадцать минут в день и, рассчитав арифметическую прогрессию, он узнал дату своей смерти и в этот же день и умер. |
| | + | |
| | + | '''Задание:''' А известно ли вам, с какой легендой связано создание геометрической прогрессии? |
| | + | |
| | + | <h2> Домашнее задание</h2> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | Посмотрите внимательно на схему, изображенную внизу, и укажите с помощью стрелочек, какому определению соответствует формула, изображенная в овале? |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | <br> |
| | + | [[Image:9kl_ArProgressia07.jpg|500x500px|пифагор]] |
| | + | <br> |
Текущая версия на 09:00, 20 мая 2015
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Арифметическая прогрессия
Определение арифметической прогрессии
Арифметической прогрессией называют такую последовательность, в которой каждый член, начиная со второго, равняется предыдущему, к которому прибавляют одно и то же число.
Число d, которое в переводе обозначает слово «разница», носит название разницы арифметической прогрессии.
Иными словами можно сказать, что арифметическая прогрессия — это числовая последовательность (аn), заданная рекуррентно соотношениями
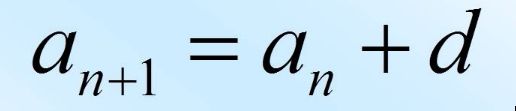
При этом n = 2, 3, 4
Где, a и d являются заданными числами.
То есть, такая числовая последовательность, как a1, a2, а3, ..., аn ... считается арифметической прогрессией.
Иначе говоря, числовая последовательность a1, a2, а3, ..., а n ... является арифметической прогрессией, если для любого натурального числа n выполняется условие an + 1 = an + d. Из этого равенства следует равенство an + 1 - an = d которая означает, что разница между любым следующим и предыдущим членами арифметической прогрессии р.
Например
Если взять последовательность чисел 4; 12; 20; 25; 36, то мы увидим, что каждое последующее число на восемь больше предыдущего. Такая последовательность получается за счет прибавления числа восемь к каждому следующему члену.
Вот такая получается арифметическая прогрессия:
• 4+8=12
• 12+8=17
• 20+8=28
• 28+8=31
Для обозначения арифметической последовательности (аn), удобной является такая запись, как:
+ a1, a2, а3, ..., аn ...
Здесь значок «+» служит заменой такого словосочетания, как «арифметическая прогрессия».
Задание
Перед вами предоставлена такая последовательность чисел:
3, 6, 9, 12, 15, 18,……
Дайте ответ на такие вопросы:
1. Можно ли назвать изображенный перечень чисел арифметической прогрессией?
2. Назовите ее первый член.
3. Чему равен ее десятый член?
4. Найдите разность этой прогрессии.
5. Какой будет сумма первых четырнадцати ее членов?
6. К какой последовательности относится эта арифметическая прогрессия? К возрастающей или убывающей?
7. Сделайте запись формулы ее n-го члена.
Формула арифметической прогрессии
Такое нахождение арифметической прогрессии, в котором чтобы вычислить аn, необходимо еще найти и 99 предшествующих членов последовательности, является не совсем удобным. Естественно, что такую вычислительную работу буден лучше выполнить при помощи формулы n-го члена, то есть осуществить аналитическое задание арифметической прогрессии.
Припустим, что первый член арифметической прогрессии равен а1, а d - разница.
Тогда:
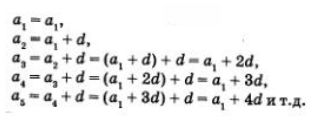
Мы видим, что в этих формулах коэффициент при числе d на один меньше порядкового номера члена прогрессии.
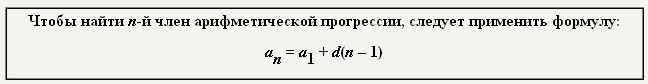

Формула суммы членов конечной арифметической прогрессии
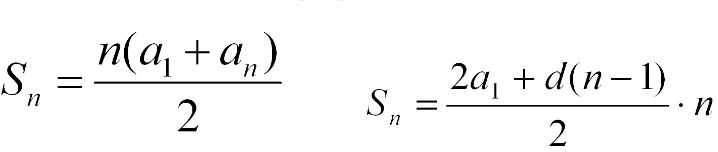
Характеристическое свойство арифметической прогрессии

Задание
Решите несколько бытовых задач:
1. По рекомендации санаторного врача, отдыхающим было рекомендовано начинать принимать загар с пяти минут, увеличивая ежедневно время пребывание на солнце, еще на пять минут. Сколько дней будет длиться путевка в санатории, если время загара увеличится до 30 минут?
2. Спортсмен за час пробегает расстояние в 10 км. Каждый следующий час бега его расстояние уменьшается на 0,5 км, чем предыдущий. За сколько времени он пробежит 50 км?
3. В театре сидячие места расположены так, что в каждом следующем ряду количество кресел на четыре больше, чем в предыдущем, а всего в зале насчитывается 1050 мест. Назовите количество рядов в зале, если первый ряд насчитывает десять кресел?
Историческая справка
А известно ли вам, что создание формулы 1-х n – членов арифметической прогрессии тесно переплетается с именем такого ученого, как Карл Фридрих Гаусс. Будучи еще совсем ребенком, он проявлял себя истинным вундеркиндом, и кроме того, что умел читать и писать, умудрялся исправлять ошибки отца в подсчетах.
Если верить легенде, то во время учебы, когда учитель предложил детям сосчитать сумму чисел от одного до ста, то восьмилетний Карл Гаусс очень быстро нашел искомую величину, так как смог заметить, что попарные суммы с противоположных сторон имеют одинаковый результат. Немного позднее он вывел формулу арифметической прогрессии.
А вот «прогрессия», как термин появился в шестом веке благодаря римлянину Боэцию и воспринимался, как бесконечная числовая последовательность. И уже древние греки из теории непрерывных пропорций выделили такие названия, как «арифметическая» и «геометрическая» прогрессия.
Задание: А вы сможете быстро подсчитать сумму от 1 до 100? Может среди нас тоже есть Гауссы-вундеркинды?
Интересные факты
В 1796 году Карл Фридрих Гаусс решил окончательно посвятить себя математике, потому что обнаружил метод, который позволил построить правильный семнадцатиугольник только с помощью линейки и циркуля! Над этой задачей бились все известные математики-геометры еще со времен великого Эвклида! А ведь изначально Гаусс собирался посвятить себя классической литературе, из-за необыкновенных склонностей к языкам.
Некоторые факты, о математических прогрессиях были известны еще древним китайским и индийским мудрецам. Так, например, есть древняя индийская легенда, которая рассказывает об изобретении шахмат, а которой проходят моменты, связанные со знаниями арифметической прогрессии.
Легенда рассказывает, как индийский шах Шерам пообещал награду тому, кто придумает интересную игр, которая вызовет длительный интерес у индийского владыки. Но мудрец Сета, который придумал шахматы, попросил за ее изобретение такое количество зерен, которое будет увеличиваться в зависимости от клеток на шахматной доске. И если на первую клеточку нужно положить только одно зернышко, то на следующую в два раза больше. И так каждый раз количество зерен на каждой следующей клетке снова удваивается по сравнению с предыдущей и т.д. вплоть до шестьдесят четвертой клетки.
Это значит, что количество зерен равняется сумме шестидесяти четырех членной геометрической прогрессии. В итоге должно было получиться такое число зерен, которое нужно было бы собирать со всей планеты. Поэтому шах просьбу ученого выполнить никак не мог.
А вот с помощью вычислений английский математик Абрахам де Муавр смог предсказать дату своей кончины. Наблюдая за продолжительностью своего сна, он заметил, что она с каждым днем увеличивается на пятнадцать минут в день и, рассчитав арифметическую прогрессию, он узнал дату своей смерти и в этот же день и умер.
Задание: А известно ли вам, с какой легендой связано создание геометрической прогрессии?
Домашнее задание
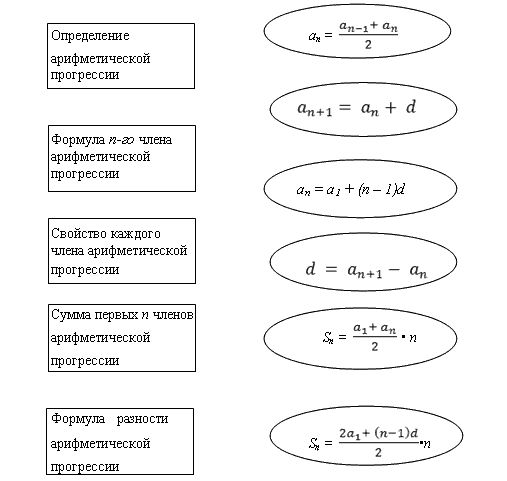
Посмотрите внимательно на схему, изображенную внизу, и укажите с помощью стрелочек, какому определению соответствует формула, изображенная в овале?
|