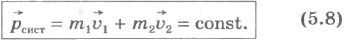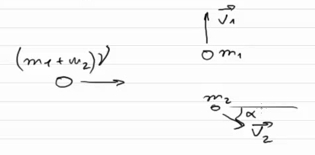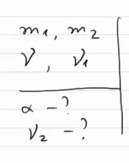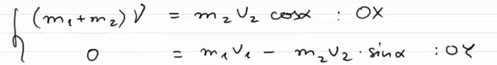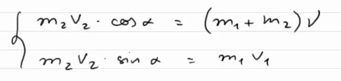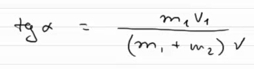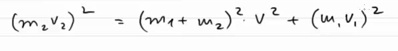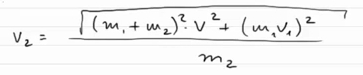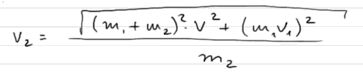Текущая версия на 18:12, 1 июня 2015

Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Закон сохранения импульса

Закон сохранения импульса

Закон сохранения импульса относится к одному из фундаментальных понятий физики. Закон сохранения импульса гласит, что если сумма внешних сил равна нулю, то импульс системы тел сохраняется.

В формульном обозначении этот закон гласит, что импульс системы, который можно представить как произведение массы на скорость для первого тела плюс произведение массы на скорость второго тела и так далее, является постоянным. То есть математическая формулировка закона сохранения импульса выглядит так:

Важно помнить, что закон сохранения импульса выполняется, если вы работаете в замкнутой системе, а замкнутая система – это система, в которой сумма внешних действующих сил будет равняться нулю.

Если у вас выполняется два этих условия, то перед вами система, в которой выполняется закон сохранения импульса.

Задача на закон сохранения импульса

Для закрепления темы на закон сохранения импульса лучше всего выполнить практическую задачу.

Задача: снаряд, который летел в горизонтальном направлении со скоростью v, разрывается на два осколка массой m1 и m2 каждый. Скорость осколка массой m1 равна v1 и направлена вертикально вверх. Необходимо определите модуль и направление скорости осколка массой m2.

Для решения этой задачи подойдет такой рисунок:

Где: • m1 + m2 – это изначальная масса снаряда со скоростью v, и он летит горизонтально вправо;
• m1 – осколок, который летит со скоростью v1 вертикально вверх;
• m2 – это осколок, который движется в некотором направлении со скоростью v2, и эту скорость нам и надо найти, а в качестве направления движения необходимо найти угол α.

Итак, что же нам дано по условию задачи: m1, m2, начальная скорость снаряда v и скорость осколка v1. А необходимо найти: угол α и скорость v2.

Для решения этой задачи необходимы две вещи:

• во-первых, необходимо задать координатные оси х и у;
• во-вторых, воспользоваться законом сохранения импульса.

Закон сохранения импульса говорит нам о том, что импульс некоторой системы в состоянии «до» точно такой же, как и импульс этот же самой системы в некотором состоянии «после».

В данном случае импульс один и тот же после разрыва снаряда. А так как кроме снаряда в нашей задаче больше не присутствуют никакое постороннее тело, то данную систему можно рассматривать, как замкнутую. А значит, в ней будет выполняться закон сохранения импульса.

Давайте запишем начальный импульс системы. До взрыва импульс системы был равен:

После взрыва системы в горизонтальном направлении х движется только отрезок m2. Значит импульс системы по оси ОХ будет равен:

А по оси ОY окажется, что начальный импульс системы равен 0, а конечный импульс системы будет равен:

В результате мы получаем систему, состоящую из двух уравнений:

Для того, чтобы было легче ее решить, перенесем влево все, что относиться к массе m2 и скорости v2, а вправо все остальное:

Теперь если поделить второе уравнение на первое, то получится, что слагаемые m2v2 сократятся, и в левой части окажется тангенс угла α.

И, исходя из этого уравнения, можно найти размер угла α.

Соответственно часть задачи, которая относится к определению направления, решена.

Теперь необходимо найти модуль значения для скорости v2. Для этого необходимо возвести в квадрат первое и второе уравнения и сложить их вместе, в результате получим:

Слева мы получаем не что иное, как основное тригонометрическое тождество с множителем m2v2 в квадрате, а справа мы получим:

Теперь необходимо выразить с левой части v2, чтобы получить ответ на задачу:

Вот такое значение скорости получается для второго осколка.

Соответственно ответами на задачу такие:

И