|
|
| (3 промежуточные версии не показаны) |
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Обозначение натуральных чисел''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Обозначение натуральных чисел''' |
| | | | |
| - | <br> | + | <h2>Натуральные числа</h2> |
| | | | |
| - | '''Обозначение натуральных чисел '''
| + | Натуральные числа – это те числа, которые применяются для подсчета различных предметов или для того, чтобы указать порядковый номер какого-либо предмета среди себе подобных или однородных. |
| | | | |
| - | <br>
| + | Записывать натуральные числа можно с помощью первых десяти цифр: |
| | | | |
| - | Для счета предметов применяют '''[[Презентація до теми Натуральний ряд чисел. Читання і запис натуральних чисел, більших за мільйон. Число 0|натуральные числа]]'''. Любое натуральное число можно записать с помощью десяти цифр: 0, 1,2, 3, 4, 5, 6, 7, 8, 9.
| + | <br> |
| | + | [[Image:5kl_Natural01.jpg|500x500px|натурчисла]] |
| | + | <br> |
| | + | |
| | + | Для записи простых натуральных чисел принято использовать позиционную десятичную систему исчисления, где значение любой цифры определяют ее местом в записи. |
| | | | |
| - | Такую запись чисел называют десятичной. Последовательность всех натуральных чисел называют натуральным рядом: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...
| + | Натуральные числа – это простейшие числа, часто используемые нами в повседневной жизни. С помощью этих чисел мы ведем подсчеты, считаем предметы, определяем их количество, порядок и номер. |
| | | | |
| - | Самое маленькое натуральное число — единица (1). В натуральном ряду каждое следующее '''[[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|число]]''' на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нем нет.
| + | С натуральными числами мы начинаем знакомиться с самого раннего детства, поэтому они для каждого из нас являются привычными и естественными. |
| | | | |
| - | Значение цифры зависит от ее места в записи числа. Например, цифра 4 означает: 4 единицы, если она стоит на последнем месте в записи числа (в разряде единиц): 4 десятка, если она стоит на предпоследнем месте (в разряде десятков), 4 сотни, если она стоит на третьем месте от конца (в разряде сотен). <br>
| + | <h2>Общее представление о натуральных числах</h2> |
| | | | |
| - | '''[[Ілюстрації: Лічба предметів. Порівняння предметів за величиною. Підготовчі вправи до написання цифр.|Цифра]]''' 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа «нуль». Это число означает «ни одного». Счет 0 : 3 футбольного матча говорит о том, что первая команда не забила ни одного гола в ворота противника. <br>
| + | Натуральные числа предназначены для несения информации о количестве предметов, их порядковом номере и множестве предметов. |
| | | | |
| - | Нуль не относят к натуральным числам. <br>
| + | Человек использует натуральные числа, так как они ему доступны как на уровне восприятия, так и на уровне воспроизведения. При озвучивании любого натурального числа, мы с вами легко его улавливаем на слух, а изобразив натуральное число – мы его видим. |
| | | | |
| - | Если запись натурального числа состоит из одного знака — одной цифры, то его называют однозначным. Например, числа 1, 5, 8 — однозначные. <br>
| + | Все натуральные числа располагаются в порядке возрастания и образуют числовой ряд, начинающийся с наименьшего натурального числа, которым является единица. |
| | | | |
| - | Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным. Например, числа 14, 33, 28, 95 — '''[[Загадка до уроку на тему «Читання, запис та порівняння чисел. Одноцифрові та двоцифрові числа. Число попереднє та наступне до даного»|двузначные]]'''. <br> | + | Если мы определились с наименьшим натуральным числом, то с наибольшим будет посложнее, так как такого числа не существует потому, что ряд натуральных чисел является бесконечным. |
| | | | |
| - | Так же по числу знаков в данном числе дают названия и другим числам:
| + | При прибавлении к натуральному числу единицы, в итоге мы получим число, которое идет за данным числом. |
| | | | |
| - | числа 386, 555, 951 — трехзначные; <br>числа 1346, 5787, 9999 — четырехзначные и т. д. <br>
| + | Такая цифра, как 0 не есть натуральным числом, а только служит для обозначения числа «ноль» и значит «ни одного». 0 означает отсутствие в десятичной записи чисел единиц данного ряда. |
| | | | |
| - | Двузначные, '''[[Порівняння способів усного додавання круглих трицифрових чисел|трехзначные]]''', четырехзначные, пятизначные и т. д. числа называют многозначными. <br>
| + | Все натуральные числа обозначаются заглавной латинской буквой N. |
| | | | |
| - | Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами. <br>
| + | <h2>Историческая справка обозначения натуральных чисел</h2> |
| | | | |
| - | Три первые цифры справа составляют класс единиц, три следующие —класс тысяч, далее идут классы миллионов, миллиардов и т. д. <br>
| + | В древние времена человек еще не знал, что такое число и как можно посчитать количество предметов. Но уже тогда возникла необходимость в счете, и человек придумал, как можно сосчитать пойманную рыбу, собранные ягоды и т.д. |
| | | | |
| - | Миллион — это тысяча тысяч (1000 тыс.), его записывают: 1 млн или 1 000 000. <br>
| + | Немного позже, древний человек пришел к тому, что нужное ему количество проще записать. Для этих целей первобытные люди стали использовать камешки, а потом палочки, которые сбереглись в римских цифрах. |
| | | | |
| - | Миллиард — это 1000 миллионов. Его записывают: 1 млрд или 1 000 000 000. <br>
| + | Следующим моментом развития системы исчисления стало использование в обозначениях некоторых чисел букв алфавита. |
| | | | |
| - | Число 15 389 000 286 записано в таблице.
| + | К первым системам исчисления относится десятичная индийская система и шестидесятеричная вавилонская. |
| | | | |
| - | Это число имеет 286 единиц в классе единиц, нуль единиц в классе тысяч, 389 единиц в классе миллионов и 15 единиц в классе миллиардов. <br>
| + | Современная система исчисления, хоть и называется арабской, но, по сути, представляет один из вариантов индийской. Правда в ее системе исчисления отсутствует цифра ноль, но арабы ее добавили, и система приобрела нынешний вид. |
| | | | |
| - | [[Image:15-06-34.jpg|550px|Обозначение натуральных чисел]]<br>
| + | <h2>Десятичная система исчисления</h2> |
| | | | |
| - | <br>Чтобы прочитать число, называют слева по очереди число единиц каждого класса и добавляют название класса. Не произносят название класса единиц, а также класса, все три цифры которого — нули. <br> | + | <br> |
| | + | [[Image:5kl_Natural02.jpg|500x500px|натурчисла]] |
| | + | <br> |
| | | | |
| - | ''Какие числа применяют для '''[[Презентація на тему: Лічба предметів|счёта]]''' предметов? <br>Назовите первые шестнадцать чисел натурального ряда, <br>Назовите все цифры. <br>Приведите примеры: двузначных чисел, трехзначных чисел, шестизначных <br>чисел. <br>Назовите разряды в классе единиц. <br>Назовите по порядку первые четыре класса в записи натуральных чисел. <br>Как читают многозначные числа? ''
| + | С натуральными числами мы уже познакомись и научились записывать их с помощью десяти цифр. Также вам уже известно, что запись чисел с использованием знаков, называется системой исчисления. |
| | | | |
| - | <br>
| + | Значение цифры в записи числа зависит от ее позиции и называется позиционным. То есть, при методах записи натуральных чисел, мы используем позиционную систему исчисления. |
| | | | |
| - | 1. Прочитайте числа 15; 152; 514; 2537; 5007; 52 615. Что означает цифра 5 в записи каждого из этих чисел? Что означает цифра 0 в записи каждого из чисел 30; 408; 50 618; 400 003?
| + | Данная система основывается на разрядности и десятичности. В десятичной системе исчисления основой для ее построения будут цифры от 0 до 9. |
| | | | |
| - | 2. Напишите число, в котором: <br>
| + | Особое место в такой системе отводится числу 10, так как, в основном счет ведется десятками. |
| | | | |
| - | а) 9 сотен 0 десятков 3 единицы; <br>б) 5 сотен 8 десятков 0 единиц; <br>в) 3 тысячи 2 сотни 4 десятка 1 единица; <br>г) 3 единицы 4 десятка 5 сотен 6 тысяч; <br>д) 9 сотен 5 десятков 0 единиц 3 тысячи; <br>е) 7 тысяч 8 единиц 0 сотен 0 десятков. <br>
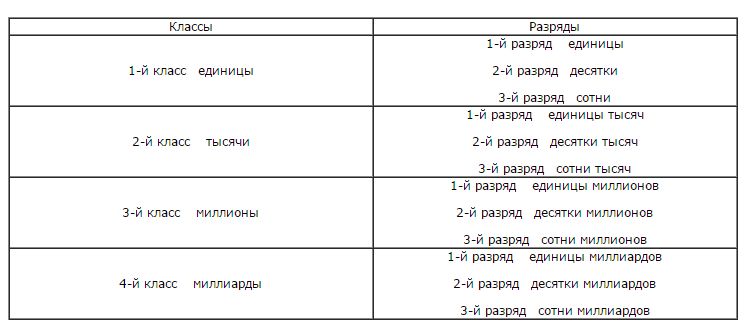
| + | '''Таблица классов и разрядов:''' |
| - | | + | |
| - | Прочитайте эти числа.
| + | |
| - | | + | |
| - | 3. Запишите цифрами числа: <br>а) восемьсот девять; <br>б) пять тысяч двести одиннадцать; <br>в) двадцать два миллиона три тысячи восемь; <br>г) двадцать восемь миллионов пятнадцать тысяч триста два; <br>д) пятьсот семь миллионов восемьдесят тысячу <br>е) один миллиард десять миллионов девять тысяч; <br>ж) четыреста двадцать три миллиарда триста сорок миллионов <br>шестьсот тысяч девятьсот восемьдесят; <br>з) пятьдесят два миллиарда восемь тысяч двенадцать; <br>и) семьсот семьдесят семь миллиардов шестьдесят восемь тысяч; <br>к) девять миллиардов пятьдесят пять тысяч.
| + | |
| - | | + | |
| - | 4. Число 580043,000707 разбивают на классы так:
| + | |
| - | | + | |
| - | 580 043 000 707 — и читают: пятьсот восемьдесят миллиардов сорок три миллиона семьсот семь. Разбейте на классы и прочитайте числа: 2407; 35810; 500215; 6570000; 3048504325; 24000670001; 300100234129.
| + | |
| - | | + | |
| - | 5. Прочитайте числа:509; 6001; 90 050; 7 000 850 127; 56 000 709 000; 21 085 000 000; 340 004 090 300; 86 820 000 800; 1 000 000 031; 63 009 000 050; 1 000 100 999; 383 365 409 707.
| + | |
| - | | + | |
| - | 6. Запишите цифрами числа:5 тыс.; 702 тыс.; 5081 тыс.; 68 303 тыс.; 12 млн; 306 млн; 487 млрд; 15 млн 205 тыс.; 65 млрд 913 млн.
| + | |
| - | | + | |
| - | 7. Запишите цифрами числа, встречающиеся в тексте:
| + | |
| - | | + | |
| - | «Миллиард — очень большое число. За тридцать лет с первого января тысяча девятьсот семидесятого года по тридцать первое декабря тысяча девятьсот девяносто девятого года прошло десять тысяч девятьсот пятьдесят семь суток, что составляет двести шестьдесят две тысячи девятьсот шестьдесят восемь часов, или девятьсот сорок шесть миллионов шестьсот восемьдесят четыре тысячи восемьсот секунд. Значит, за тридцать лет не проходит и миллиарда секунд».
| + | |
| - | | + | |
| - | 8. Запищите пять раз подряд цифру 6.
| + | |
| - | | + | |
| - | Прочитайте получившееся число.
| + | |
| - | | + | |
| - | 9. Запишите пять раз подряд число 80.
| + | |
| - | | + | |
| - | Прочитайте получившееся число.
| + | |
| - | | + | |
| - | 10. Прочитайте число, которое получится, если число 674 записать подряд: <br>
| + | |
| - | | + | |
| - | а) два раза;<br>
| + | |
| - | | + | |
| - | б) три раза; <br>
| + | |
| - | | + | |
| - | в) четыре раза.
| + | |
| - | | + | |
| - | 11. Запишите все трехзначные числа, для записи которых употребляются только цифры 1 и 2. <br>Решение. В записи числа на первом слева месте (в разряде сотен) может стоять цифра 1 или цифра 2:<br>
| + | |
| - | | + | |
| - | {| width="200" border="1" cellspacing="1" cellpadding="1"
| + | |
| - | |-
| + | |
| - | | 1<br>
| + | |
| - | | <br>
| + | |
| - | | <br>
| + | |
| - | |}
| + | |
| - | | + | |
| - | или <br>
| + | |
| - | | + | |
| - | {| width="200" border="1" cellspacing="1" cellpadding="1"
| + | |
| - | |-
| + | |
| - | | 2<br>
| + | |
| - | | <br>
| + | |
| - | | <br>
| + | |
| - | |}
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | [[Image:15-06-35.jpg|550px|Обозначение натуральных чисел]]
| + | |
| - | | + | |
| - | <br>На третьем месте (в разряде единиц) в каждом из полученных четырех случаев также можно записать либо 1, либо 2:
| + | |
| - | | + | |
| - | [[Image:15-06-36.jpg|480px|Обозначение натуральных чисел]]<br><br>Получили восемь чисел: 111, 112, 121, 122, 211, 212, 221, 222.
| + | |
| - | | + | |
| - | 12. Запишите все трехзначные числа, для записи которых употребляются только цифры 0 и 7.
| + | |
| - | | + | |
| - | Найдите [http://xvatit.com/busines/ '''сумму'''] этих чисел и разделите ее на 211. <br><br>13. Прочитайте числа
| + | |
| - | | + | |
| - | 380; 907; 60 239; 102 400; 999 999.
| + | |
| - | | + | |
| - | 14. Сколько десятков в сотне? Сколько сотен в тысяче? Сколько десятков в тысяче? Сколько тысяч в миллионе?
| + | |
| - | | + | |
| - | 15. Сколько цифр использовано для записи числа 640 046? Сколько из них различных?
| + | |
| - | | + | |
| - | 16. Назовите число:
| + | |
| - | | + | |
| - | а) следующее за числом 99; <br>б) предшествующее числу 300; <br>в) следующее за числом 19 999;
| + | |
| - | | + | |
| - | г) предшествующее числу 1200; <br>д) на 1 меньшее числа 700; <br>е) на 1 большее числа 8999.
| + | |
| - | | + | |
| - | 17. Назовите порядок действий и устно вычислите:
| + | |
| - | | + | |
| - | а) 1260 - 120 : 2; в) (500 - 100 + 200) : (301 - 300); <br>б) (5003 - 7) • (300 - 300); г) 20 • 10 : 2.
| + | |
| - | | + | |
| - | 18. Найдите сумму:
| + | |
| - | | + | |
| - | а) 60 000 + 7000 + 300 + 50 + 9; <br>б) 4 000 000 + 70 000 + 8000 + 600 + 5; <br>в) 900 000 + 3000 + 700 + 20; <br>г) 8000 + 600 + 1.
| + | |
| - | | + | |
| - | 19. Один комбайнер намолотил 231 т зерна, а второй — на 46 т меньше. Сколько зерна намолотили оба комбайнера?
| + | |
| - | | + | |
| - | 20. Масса яблока 140 г, а масса груши на 60 г больше. Какова масса трех таких яблок и груши?
| + | |
| - | | + | |
| - | 21. Расстояние от дома до школы 370 м, а расстояние от дома до стадиона 1240 м. На сколько метров расстояние от дома до школы меньше расстояния от дома до стадиона?
| + | |
| - | | + | |
| - | 22. Выполните действия:
| + | |
| - | | + | |
| - | а) 654 + 367; г) 987 : 7; ж) 192 : 32 + 8; <br>б) 947 - 469; д) 3018 : 6; з) 28 • (319 - 273). <br>в) 258 • 8; е) 52 • 23 - 77;
| + | |
| - | | + | |
| - | 23. Запишите натуральное число:
| + | |
| - | | + | |
| - | а) следующее за числом 999; <br>б) на 1 меньшее 1000; <br>в) предшествующее числу 1 000 000; <br>г) на 1 большее числа 999 999 999; <br>д) на 1 меньшее числа 56 300.
| + | |
| - | | + | |
| - | 24. Запишите цифрами число:
| + | |
| - | | + | |
| - | а) двадцать четыре; <br>б) двести сорок; <br>в) шестьсот двадцать семь тысяч триста; <br>г) три миллиона восемьсот тысяч четыре; <br>д) четыреста миллионов семьдесят тысяч двести шесть; <br>е) девяносто пять миллиардов триста восемь миллионов шестьсот тысяч семьсот сорок пять; <br>ж) десять миллиардов сто миллионов семьдесят пять тысяч три; <br>з) девять миллиардов пять тысяч шесть.
| + | |
| - | | + | |
| - | 25. Запишите цифрами числа: 86 тыс.; 11 млн; 367 млрд.
| + | |
| - | | + | |
| - | 26. Напишите девять раз подряд цифру 4. Запишите словами получившееся число.
| + | |
| - | | + | |
| - | 27. Запишите все двузначные числа, в запись которых входят лишь цифры 2 и 3. Найдите сумму этих чисел.
| + | |
| - | | + | |
| - | 28. На одной ферме 847 коров, а на другой — на 309 коров больше. Сколько коров на двух фермах?
| + | |
| - | | + | |
| - | 29. Расстояние от школы до кинотеатра 650 м, а от кинотеатра до дома 830 м. На сколько расстояние от школы до кинотеатра меньше расстояния от кинотеатра до дома?
| + | |
| - | | + | |
| - | 30. Выполните действия:
| + | |
| - | | + | |
| - | а) 245 + 35 • 18; в) 10 260 : 36 + 164; <br>б) (87 + 35) • 25; г) 52 998 : (37 + 29). <br>
| + | |
| - | | + | |
| - | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br>
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub>
| + | |
| - | | + | |
| - | <br>
| + | |
| - | | + | |
| - | '''<u>Содержание урока</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии
| + | |
| | | | |
| - | '''<u>Практика</u>'''
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения
| + | [[Image:5kl_Natural03.jpg|500x500px|натурчисла]] |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| - | | + | |
| - | <br> | + | |
| - | | + | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | Так, например, 10 единиц объединены в десятки, далее в сотни, тысячи и тому подобное. |
| | + | Поэтому число 10 является основанием системы исчисления и носит название десятичной системы исчисления. |
Натуральные числа – это те числа, которые применяются для подсчета различных предметов или для того, чтобы указать порядковый номер какого-либо предмета среди себе подобных или однородных.
Для записи простых натуральных чисел принято использовать позиционную десятичную систему исчисления, где значение любой цифры определяют ее местом в записи.
Натуральные числа – это простейшие числа, часто используемые нами в повседневной жизни. С помощью этих чисел мы ведем подсчеты, считаем предметы, определяем их количество, порядок и номер.
С натуральными числами мы начинаем знакомиться с самого раннего детства, поэтому они для каждого из нас являются привычными и естественными.
Натуральные числа предназначены для несения информации о количестве предметов, их порядковом номере и множестве предметов.
Человек использует натуральные числа, так как они ему доступны как на уровне восприятия, так и на уровне воспроизведения. При озвучивании любого натурального числа, мы с вами легко его улавливаем на слух, а изобразив натуральное число – мы его видим.
Все натуральные числа располагаются в порядке возрастания и образуют числовой ряд, начинающийся с наименьшего натурального числа, которым является единица.
Если мы определились с наименьшим натуральным числом, то с наибольшим будет посложнее, так как такого числа не существует потому, что ряд натуральных чисел является бесконечным.
При прибавлении к натуральному числу единицы, в итоге мы получим число, которое идет за данным числом.
Такая цифра, как 0 не есть натуральным числом, а только служит для обозначения числа «ноль» и значит «ни одного». 0 означает отсутствие в десятичной записи чисел единиц данного ряда.
Все натуральные числа обозначаются заглавной латинской буквой N.
В древние времена человек еще не знал, что такое число и как можно посчитать количество предметов. Но уже тогда возникла необходимость в счете, и человек придумал, как можно сосчитать пойманную рыбу, собранные ягоды и т.д.
Немного позже, древний человек пришел к тому, что нужное ему количество проще записать. Для этих целей первобытные люди стали использовать камешки, а потом палочки, которые сбереглись в римских цифрах.
Следующим моментом развития системы исчисления стало использование в обозначениях некоторых чисел букв алфавита.
К первым системам исчисления относится десятичная индийская система и шестидесятеричная вавилонская.
Современная система исчисления, хоть и называется арабской, но, по сути, представляет один из вариантов индийской. Правда в ее системе исчисления отсутствует цифра ноль, но арабы ее добавили, и система приобрела нынешний вид.
С натуральными числами мы уже познакомись и научились записывать их с помощью десяти цифр. Также вам уже известно, что запись чисел с использованием знаков, называется системой исчисления.
Значение цифры в записи числа зависит от ее позиции и называется позиционным. То есть, при методах записи натуральных чисел, мы используем позиционную систему исчисления.
Данная система основывается на разрядности и десятичности. В десятичной системе исчисления основой для ее построения будут цифры от 0 до 9.
Особое место в такой системе отводится числу 10, так как, в основном счет ведется десятками.
Так, например, 10 единиц объединены в десятки, далее в сотни, тысячи и тому подобное.
Поэтому число 10 является основанием системы исчисления и носит название десятичной системы исчисления.