|
|
|
| (3 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 11 класс, Геометрия, урок, на Тему, Объем призмы</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 11 класс, Геометрия, урок, на Тему, Объем призмы, плоскость, объем, параллелепипед, призма</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 11 класс|Математика 11 класс]]>>Математика:Объем призмы''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 11 класс|Математика 11 класс]]>>Математика:Объем призмы''' |
| | | | |
| | + | <br> '''Объем призмы''' |
| | | | |
| - | '''ОБЪЕМ ПРИЗМЫ'''
| + | <h2>Чему равен объем призмы и как его найти</h2> |
| | | | |
| - | <br>Рассмотрим сначала треугольную призму (рис. 478). Дополним ее до параллелепипеда, как указано на рисунке. Точка О является центром симметрии параллелепипеда. Поэтому достроенная призма симметрична исходной относительно точки О, следовательно, имеет объем, равный объему исходной призмы. Таким образом, объем построенного параллелепипеда равен удвоенному'объему данной призмы.
| + | Объём призмы - это произведение площади ее основания на высоту. |
| | | | |
| - | Объем параллелепипеда равен произведению площади его основания на высоту. Площадь его основания равна удвоенной площади треугольника ABC, а высота равна высоте исходной призмы. Отсюда заключаем, что объем исходной призмы равен произведению площади ее основания на высоту.<br>
| + | Однако нам известно, что у основания призмы может быть треугольник, квадрат или какой-либо другой многогранник. |
| | | | |
| - | [[Image:2-07-64.jpg]]
| + | Следовательно, для нахождения объема призмы, необходимо просто вычислить площадь основания призмы, а потом эту площадь умножить на ее высоту. |
| | | | |
| | + | То есть, если у основания призмы треугольник, то значит вначале нужно найти площадь треугольника. Если же основанием призмы является квадрат или другой многоугольник, то значит вначале нужно искать площадь квадрата или же другого многоугольника. |
| | | | |
| | + | Следует помнить, что высотой призмы является перпендикуляр, проведенный к основаниям призмы. |
| | | | |
| - | [[Image:2-07-65.jpg]]<br> <br>Рассмотрим теперь произвольную призму (рис. 479). Разобьем ее основание на треугольники. Пусть [[Image:21-06-11.jpg]] — один из этих треугольников. Проведем через произвольную точку X треугольника [[Image:21-06-11.jpg]] прямую, параллельную боковым ребрам. Пусть а, — отрезок этой прямой, принадлежащий призме. Когда точка X описывает треугольник [[Image:21-06-11.jpg]], отрезки а, заполняют треугольную призму. Построив такую призму для каждого треугольника [[Image:21-06-11.jpg]], мы получим разбиение данной призмы на треугольные. Все эти призмы имеют одну и ту же высоту, равную высоте исходной призмы.
| + | <h2>Что такое призма</h2> |
| | | | |
| - | Объем данной призмы равен сумме объемов треугольных призм, ее составляющих. По доказанному объем треугольной призмы равен произведению площади ее основания на высоту. Отсюда следует, что объем исходной призмы равен:
| + | А теперь давайте вспомним определение призмы. |
| | | | |
| - | <br>V=S<sub>1</sub>H+S<sub>2</sub>H+... + S<sub>n</sub>H=(S<sub>1</sub>+S<sub>2</sub> + ... + S<sub>n</sub>)H,
| + | Призма – это многоугольник, две грани (основания) которого, находятся в параллельных плоскостях, а все ребра, находящиеся вне этих граней параллельны. |
| | | | |
| - | <br>где S<sub>1</sub>, S<sub>2</sub>, S<sub>n</sub> —площади треугольников, на которые разбито основание призмы, а H — высота призмы. Сумма площадей треугольников равна площади S основания данной призмы. Поэтому
| + | Если говорить проще, то: |
| | | | |
| - | V=SH.
| + | Призма – это любая геометрическая фигура, которая имеет два основания, равных между собой и плоские грани. |
| | | | |
| - | '''''Итак, обтъем любой призмы равен произведению площади ее основания на высоту.'''''
| + | Название призмы зависит от формы ее основания. Когда основанием призмы является треугольник, то такую призму называют треугольной. Многогранной призмой называют геометрическую фигуру, основанием которой является многогранник. Также призма - это разновидность цилиндра. |
| | | | |
| - | Задача (24). В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите объем призмы, если площадь сечения Q, а боковые ребра равны I.
| + | <h2>Каких видов бывают призмы</h2> |
| | | | |
| - | Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 480). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а высота равна I. Эта призма имеет тот же объем. Таким образом, объем исходной призмы равен QI.<br><br><br><br>
| + | <br> |
| | + | [[Image:11kl_Prizma01.jpg|500x500px|призма]] |
| | + | <br> |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| + | Если мы посмотрим на рисунок вверху, то увидим, что призмы бывают прямыми, правильными и наклонными. |
| | | | |
| - | <sub>Математика за 11 класс бесплатно [[Математика|скачать]], планы конспектов уроков, готовимся к школе [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>
| + | '''Задание''' |
| | | | |
| - | <br> | + | 1. Какую призму называют правильной?<br> |
| | + | 2. Почему она так называется?<br> |
| | + | 3. Какое носит название призма, основаниями которой являются правильные многоугольники?<br> |
| | + | 4. Что является высотой этой фигуры?<br> |
| | + | 5. Как называют призму, ребра которой не являются перпендикулярными?<br> |
| | + | 6. Дайте определение треугольной призме.<br> |
| | + | 7. Может ли призма быть параллелепипедом?<br> |
| | + | 8. Какая геометрическая фигура называется полуправильным многоугольником?<br> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | <h2>Из каких элементов состоит призма</h2> |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | [[Image:11kl_Prizma02.jpg|500x500px|призма]] |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| | | | |
| - | '''<u>Иллюстрации</u>'''
| + | Призма состоит из таких элементов, как нижнее и верхнее основание, боковые грани, ребра и вершины. |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | • Оба основания призмы лежат в плоскостях и параллельны друг другу.<br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | • Боковые грани пирамиды – это параллелограммы.<br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | • Боковая поверхность пирамиды является суммой боковых граней.<br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | • Общие стороны боковых граней, есть не что иное, как боковые ребра данной фигуры.<br> |
| | + | • Высотой пирамиды является отрезок, соединяющий плоскости оснований и перпендикулярен им.<br> |
| | + | |
| | + | <h2>Свойства призмы</h2> |
| | + | |
| | + | Геометрическая фигура, как призма, обладает рядом свойств. Давайте более подробно рассмотрим эти свойства: |
| | + | |
| | + | • Во-первых, основаниями призмы называются равные многоугольники;<br> |
| | + | • Во-вторых, у призмы боковые грани представлены в виде параллелограмма;<br> |
| | + | • В-третьих, у этой геометрической фигуры ребра параллельны и равны;<br> |
| | + | • В-четвертых, площадью полной поверхности призмы является:<br> |
| | + | |
| | + | <br> |
| | + | [[Image:11kl_Prizma03.jpg|500x500px|призма]] |
| | + | <br> |
| | | | |
| - | '''<u>Дополнения</u>'''
| + | А теперь рассмотрим теорему, которая предоставляет формулу, с помощью которой вычисляют площадь боковой поверхности и доказательство. |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | <br> |
| | + | [[Image:11kl_Prizma04.jpg|500x500px|призма]] |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | <h2>Интересные факты о призме</h2> |
| | + | |
| | + | Задумывались ли вы над таким интересным фактом, что призмой может быть не только, геометрическое тело, но и другие окружающие нас предметы. Даже обычная снежинка в зависимости от температурного режима может превратиться в ледяную призму, приняв форму шестигранной фигуры. |
| | + | |
| | + | А вот кристаллы кальцита обладают таким уникальным явлением, как распадаться на осколки и приобретать форму параллелепипеда. И что самое удивительное, на какие бы мелкие части не дробили кристаллы кальцита, результат всегда одинаковый, они превращаются в махонькие параллелепипеды. |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | Оказывается, призма получила популярность не только в математике, демонстрируя свое геометрическое тело, но и в области искусства, так как она является основой картин, созданных такими великими художниками, как П.Пикассо, Брак, Грисс и других. |
Текущая версия на 14:52, 8 июня 2015
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Объем призмы
Объем призмы
Чему равен объем призмы и как его найти
Объём призмы - это произведение площади ее основания на высоту.
Однако нам известно, что у основания призмы может быть треугольник, квадрат или какой-либо другой многогранник.
Следовательно, для нахождения объема призмы, необходимо просто вычислить площадь основания призмы, а потом эту площадь умножить на ее высоту.
То есть, если у основания призмы треугольник, то значит вначале нужно найти площадь треугольника. Если же основанием призмы является квадрат или другой многоугольник, то значит вначале нужно искать площадь квадрата или же другого многоугольника.
Следует помнить, что высотой призмы является перпендикуляр, проведенный к основаниям призмы.
Что такое призма
А теперь давайте вспомним определение призмы.
Призма – это многоугольник, две грани (основания) которого, находятся в параллельных плоскостях, а все ребра, находящиеся вне этих граней параллельны.
Если говорить проще, то:
Призма – это любая геометрическая фигура, которая имеет два основания, равных между собой и плоские грани.
Название призмы зависит от формы ее основания. Когда основанием призмы является треугольник, то такую призму называют треугольной. Многогранной призмой называют геометрическую фигуру, основанием которой является многогранник. Также призма - это разновидность цилиндра.
Каких видов бывают призмы
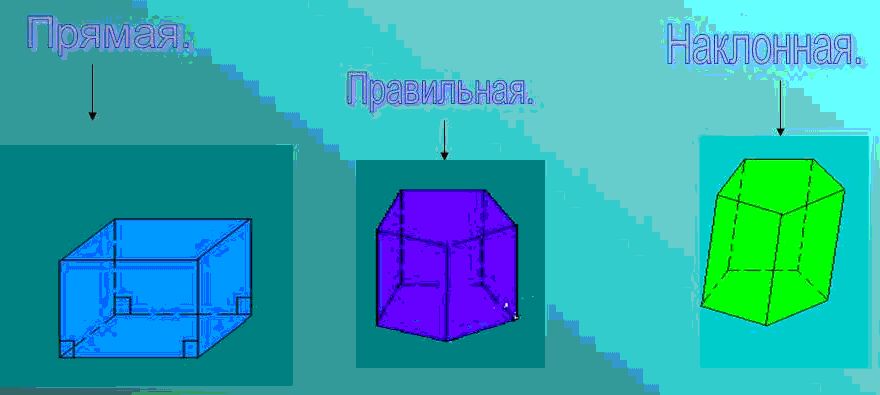
Если мы посмотрим на рисунок вверху, то увидим, что призмы бывают прямыми, правильными и наклонными.
Задание
1. Какую призму называют правильной?
2. Почему она так называется?
3. Какое носит название призма, основаниями которой являются правильные многоугольники?
4. Что является высотой этой фигуры?
5. Как называют призму, ребра которой не являются перпендикулярными?
6. Дайте определение треугольной призме.
7. Может ли призма быть параллелепипедом?
8. Какая геометрическая фигура называется полуправильным многоугольником?
Из каких элементов состоит призма
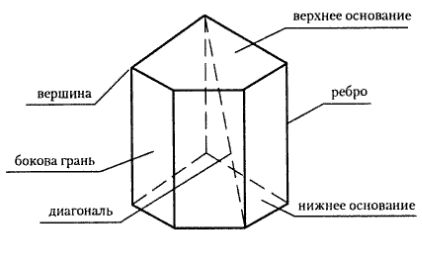
Призма состоит из таких элементов, как нижнее и верхнее основание, боковые грани, ребра и вершины.
• Оба основания призмы лежат в плоскостях и параллельны друг другу.
• Боковые грани пирамиды – это параллелограммы.
• Боковая поверхность пирамиды является суммой боковых граней.
• Общие стороны боковых граней, есть не что иное, как боковые ребра данной фигуры.
• Высотой пирамиды является отрезок, соединяющий плоскости оснований и перпендикулярен им.
Свойства призмы
Геометрическая фигура, как призма, обладает рядом свойств. Давайте более подробно рассмотрим эти свойства:
• Во-первых, основаниями призмы называются равные многоугольники;
• Во-вторых, у призмы боковые грани представлены в виде параллелограмма;
• В-третьих, у этой геометрической фигуры ребра параллельны и равны;
• В-четвертых, площадью полной поверхности призмы является:
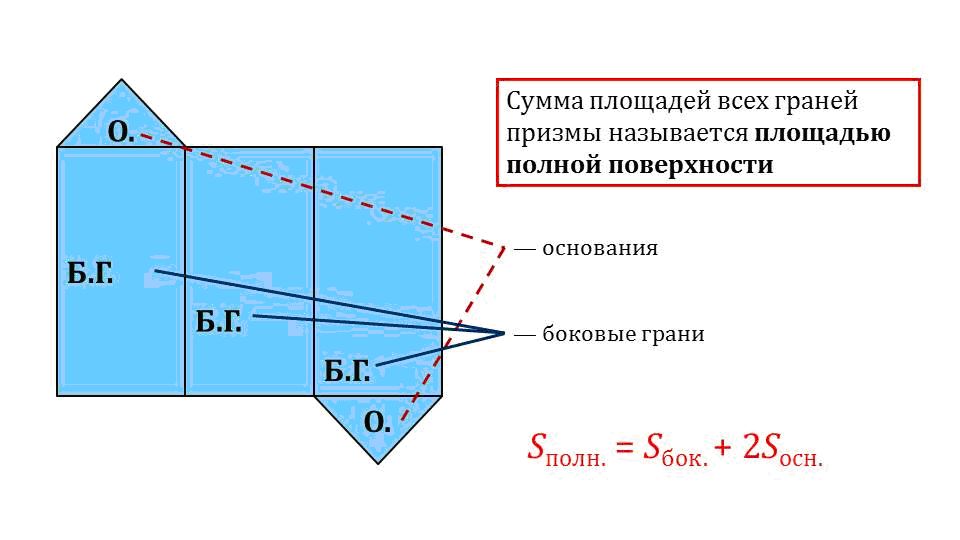
А теперь рассмотрим теорему, которая предоставляет формулу, с помощью которой вычисляют площадь боковой поверхности и доказательство.

Интересные факты о призме
Задумывались ли вы над таким интересным фактом, что призмой может быть не только, геометрическое тело, но и другие окружающие нас предметы. Даже обычная снежинка в зависимости от температурного режима может превратиться в ледяную призму, приняв форму шестигранной фигуры.
А вот кристаллы кальцита обладают таким уникальным явлением, как распадаться на осколки и приобретать форму параллелепипеда. И что самое удивительное, на какие бы мелкие части не дробили кристаллы кальцита, результат всегда одинаковый, они превращаются в махонькие параллелепипеды.
Оказывается, призма получила популярность не только в математике, демонстрируя свое геометрическое тело, но и в области искусства, так как она является основой картин, созданных такими великими художниками, как П.Пикассо, Брак, Грисс и других.
|














