KNOWLEDGE HYPERMARKET

Параллелограмм. Полные уроки
 
(3 промежуточные версии не показаны)
Строка 4: Строка 4:
<metakeywords>Гипермаркет знаний, Геометрия, Планиметрия, 8 класс, Параллелограмм</metakeywords>
<metakeywords>Гипермаркет знаний, Геометрия, Планиметрия, 8 класс, Параллелограмм</metakeywords>
-
==Тема урока==
+
'''Параллелограмм'''
-
*'''Параллелограмм'''
+
-
== Цели урока ==
+
<h2>Цели урока</h2>
-
*Образовательные – повторение, обобщение и проверка знаний по теме: “параллелограмм”; выработка основных навыков.
+
• Познакомить школьников с определением параллелограмма;<br>
-
*Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
+
• Углубить знания учеников о понятии параллелограмма;<br>
-
*Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
+
• Сформировать знания о понятиях и признаках параллелограмма;<br>
 +
• Закрепить навыки построения этой геометрической фигуры;<br>
 +
• Познакомить с формулой для вычисления площади параллелограмма;<br>
 +
• Научить детей применять формулы во время решения задач.<br>
-
== Задачи урока ==
+
<h2>Задачи урока</h2>
-
*Проверить умение учащихся решать задачи.
+
• Расширить знания школьников о геометрических фигурах;<br>
 +
• Продолжить обучать применять свойства параллелограмма при решении задач;<br>
 +
• Развивать познавательный интерес детей к урокам геометрии;<br>
 +
• Воспитывать любознательность, умение анализировать и выражать свои мысли математическим языком;<br>
 +
• Повторить пройденные материалы о геометрических фигурах.<br>
 +
• Воспитывать внимательность, усидчивость и желание учиться.<br>
-
== План урока ==
+
<h2>План урока</h2>
-
#Введение.  
+
1. Ознакомление с параллелограммом, как одной из главных геометрических фигур.<br>
-
#Частные виды параллелограмма.  
+
2. Свойства параллелограмма.<br>
-
#Теоретическая часть.  
+
3. Признаки параллелограмма.<br>
-
#Практическая часть.  
+
4. Частные виды параллелограмма.<br>
-
#Дополнительный материал.
+
5. Площадь параллелограмма.<br>
 +
6. Дополнительный материал.<br>
 +
7. Домашнее задание.<br>
-
=== Введение ===
+
<h2>Определение. Основные сведения о параллелограмме</h2>
-
Для начала я решил узнать, откуда&nbsp; появилось определение параллелограмма. Оказывается термин «параллелограмм» греческого происхождения и, согласно древнегреческому философу '''Проклу''', был введен '''Евклидом'''. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.<br>
+
Параллелограммом является четырехугольник с попарно параллельными противоположными сторонами.
-
В «Началах» Евклида доказывается следующая теорема: '''в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам'''. Евклид не упоминает о том, что '''точка пересечения диагоналей параллелограмма делит их пополам'''. Он не рассматривает ни прямоугольника, ни ромба.  
+
Параллелограммы составляют наибольший класс четырехугольников.  
-
'''Полная теория параллелограммов была разработана к концу средних веков и появились в учебниках лишь в XVII веке.''' Все теоремы о параллелограммах основываются непосредственно или косвенно на '''теореме Евклида о свойствах&nbsp; параллелограмма'''.  
+
<br>
 +
[[Image:8kl_parallelogr01.jpg|300x300px|параллелограмм]]
 +
<br>
 +
 +
У параллелограмма, как и у любой геометрической фигуры, имеются основание и высота. Основанием данной фигуры являются какие угодно 2 противоположные стороны. Высотой параллелограмма называют расстояние между его основаниями. С каждой вершины данной фигуры есть возможность прочертить по две высоты.  
-
Само же понятие параллелограмм от греч. '''Parallelos — параллельный''' и '''gramme — линия'''. Поэтому слово «параллелограмм» можно перевести как «'''параллельные линии'''».
+
Сам термин «параллелограмм» имеет греческое происхождение и был выведен известным древнегреческим философом и математиком – Евклидом. О параллелограмме и кое-каких его свойствах знали еще пифагорейцы.  
 +
В своем знаменитом писании «Начала», Евклид доказал теорему из которой следует, что в данной геометрической фигуре противоположные стороны и углы равны, а диагональ делит параллелограмм пополам.
-
=== Частные виды параллелограмма ===
+
Полная теория об этой геометрической фигуре появилась только к концу средних веков и то была основана, благодаря теоремам Евклида.
-
'''Известны некоторые виды параллелограмма:&nbsp;'''<br>
+
Если термин «параллелограмм» перевести дословно, то он произошел от греческих слов параллельный и линия, поэтому и переводится как «параллельные линии».
-
#''Прямоугольник.''
+
<h2>Свойства параллелограмма</h2>
-
#''Ромб.''
+
-
#''Квадрат.''
+
-
<br>'''Прямоугольник '''- параллелограмм, все углы которого прямые. Прямоугольник имеет все свойства параллелограмма, но так же&nbsp; имеет свое собственное: '''Диагонали прямоугольника равны'''.<br>
+
А теперь давайте рассмотрим свойства, присущи данной фигуре. Значит, в параллелограмме:
-
[[Image:28032011 0.jpg|200px|Прямоугольник]]
+
• Противоположные стороны равны;<br>
-
 
+
• противоположные углы, токже равны;<br>
-
''Прямоугольник''
+
• сумма углов, прилегающих к одной стороне, равняется 180 градусов;<br>
-
 
+
• сумма всех углов будет 360 градусов;<br>
-
<br>'''Ромб '''- параллелограмм, все стороны которого равны. Ромб обладает очень важным индивидуальным свойством: '''Диагонали ромба взаимно перпендикулярны и делят его углы пополам'''.<br>
+
• диагонали пересекаются, и разделяются точкой пересечения пополам;<br>
-
 
+
• диагонали разделяют параллелограмм на 2треугольника, которые равны между собой;<br>
-
[[Image:28032011 1.jpg|200px|Ромб]]
+
• точка пересечения диагоналей будет его центром симметрии;<br>
-
 
+
• диагонали и стороны данной фигуры связаны следующим соотношением:<br>
-
''Ромб''<br>
+
-
 
+
-
Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Ромб связывали первоначально с сечением, проведенным в обмотанном веретене. <br><br>'''Квадрат '''- равносторонний прямоугольник (или параллелограмм, у которого все углы прямые, стороны равны между собой; или ромб, у которого все углы прямые). Так как квадрат является и ромбом, и прямоугольником, и&nbsp; параллелограммом он имеет все свойства вышеперечисленных фигур.<br>
+
-
 
+
-
[[Image:28032011 2.jpg|200px|Квадрат]]
+
-
 
+
-
''Квадрат''<br>
+
-
 
+
-
Термин «квадрата» происходит от латинского quadratum (quadrare - сделать четырехугольным), перевод с греческого “тетрагонон” - '''четырехугольник'''. <br>
+
-
 
+
-
===Теоретическая часть ===
+
-
 
+
-
==== Определения  ====
+
-
 
+
-
'''Параллелограмм '''(от греч. parallelos — параллельный и gramme — линия) — это четырёхугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.<br>
+
-
 
+
-
[[Image:28032011 7.jpg|200px|Параллелограмм]]
+
-
 
+
-
 
+
-
'''Параллелограмм '''— четырехугольник, у которого противоположные стороны попарно параллельны.&nbsp;<br> '''Параллелограмм '''— всякий четырехугольник, противоположные стороны которого попарно равны и параллельны; преимуществ. так назыв. удлиненный четырехугольник, с двумя острыми и двумя тупыми углами; прочие же виды параллелогр. имеют свои особ. названия (ромб, квадрат, прямоугольник).
+
-
 
+
-
[[Image:28032011 8.jpg|200px|Параллелограмм]]
+
-
 
+
-
 
+
-
'''Параллелограмм''', четырехугольник (четырехсторонняя плоская фигура), у которого каждая пара противоположных сторон параллельна. У параллелограмма противоположные стороны и противоположные углы равны. Площадь параллелограмма равна произведению одной стороны на длину перпендикуляра, опущенного на нее с противоположной стороны. Параллелограмм, у которого все стороны равны, называется ромбом.<br>&nbsp;'''Параллелограмм '''- четырехугольник, каждая пара противоположных сторон которого параллельны и равны между собой.
+
-
 
+
-
''Все эти определения верны и по своему дополняют друг друга.''
+
-
 
+
-
 
+
-
==== Свойства параллелограмма  ====
+
-
 
+
-
 
+
-
*'''Теорема. Противоположные стороны параллелограма равны.'''<br>''Доказательство''. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠САВ=∠АСD, ∠АСВ=∠DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников.<br>
+
-
 
+
-
*'''Теорема. Противоположные углы параллелограмма равны: '''∠'''А='''∠'''С и '''∠'''В='''∠'''D.'''<br>Равенство первой пары идет из равенства треугольников АВD и CBD, а второй - АВС и ACD.<br>
+
-
 
+
-
*'''Теорема. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.'''<br>Это так, потому что они являются внутренними односторонними углами.<br>
+
-
 
+
-
*'''Теорема. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.'''<br>''Доказательство''. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ОАD=∠ОСВ и ∠ОDА=∠ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
+
<br>
<br>
 +
[[Image:8kl_parallelogr02.jpg|200x200px|параллелограмм]]
 +
<br>
 +
 +
• угол между высотами будет равен его острому углу;<br>
 +
• биссектрисы 2-х противоположных углов параллельны.<br>
{{#ev:youtube|GwYUP0mgP2Y}}
{{#ev:youtube|GwYUP0mgP2Y}}
Строка 100: Строка 78:
{{#ev:youtube|s1T3yZZXZR4}}  
{{#ev:youtube|s1T3yZZXZR4}}  
 +
<h2>Признаки параллелограмма</h2>
-
==== Признаки параллелограмма ====
+
Для определения будет ли данная фигура параллелограммом имеется ряд признаков. Разберем 3 основных признака параллелограмма:
-
*Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
+
1. Когда четырехугольник имеет стороны, из которых две равные и две параллельные, то данный четырехугольник будет параллелограммом;<br>
-
*Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
+
-
*Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
+
-
*Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
+
-
*Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника KLMN являются вершинами параллелограмма Вариньона.
+
-
[[Image:28032011 5.png|200px|Параллелограмм]]
+
2. В случае, когда четырехугольник имеет попарно равные противоположные стороны, то он - параллелограмм;<br>
-
*Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника ABCD. Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.
+
3. Также, данная фигура будет параллелограммом, когда у четырехугольника его диагонали пересекаются, а точка пересечения разделяет их пополам.<br>
-
*'''Теорема. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.'''<br>Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом.<br>В геометрии рассматривают частные случаи параллелограмма: прямоугольник, ромб, квадрат. <br>
+
<h2>Частные виды параллелограмма</h2>
-
 
+
-
*'''Теорема. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.'''<br>Пусть ∠А=∠С и ∠В=∠D. Т.к. ∠А+∠В+∠С+∠D=360<sup>о</sup>, то ∠А+∠В=180<sup>о</sup> и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.<br>
+
-
 
+
-
*'''Теорема. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.'''<br>Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.<br>
+
-
 
+
-
*'''Теорема. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.'''<br>Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
+
-
 
+
-
*'''Теорема. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник - параллелограмм.'''<br>Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом.<br>
+
 +
<br>
 +
[[Image:8kl_parallelogr03.jpg|500x500px|параллелограмм]]
 +
<br>
{{#ev:youtube|oUTSc_qzFqs}}
{{#ev:youtube|oUTSc_qzFqs}}
-
 
{{#ev:youtube|G3SLidg2_Ak}}  
{{#ev:youtube|G3SLidg2_Ak}}  
 +
 +
В частных случаях параллелограммом могут быть и такие геометрические фигуры, как
 +
ромб, прямоугольник или квадрат.
 +
Давайте вспомним, что собой представляют эти фигуры и дадим им определения.
-
=== Практическая часть  ===
+
'''Задание:'''
-
==== Задача №1 ====
+
1. Какую фигуру принято называть прямоугольником?<br>
 +
2. Какие он имеет свойства?<br>
 +
3. Совпадают ли эти свойства со свойствами параллелограмма?<br>
 +
4. Дайте определение такой геометрической фигуры, как квадрат?<br>
 +
5. Дайте определение ромба. Перечислите его свойства и признаки.<br>
 +
6. Докажите, что квадрат - это частный случай параллелограмма.<br>
-
'''Высоты параллелограмма равны 5см и 4см, а периметр равен 42см. Найдите площадь параллелограмма.'''  
+
'''Задачи 1.'''
-
'''Решение.'''
+
На первом рисунке дан треугольник АВС. Параллельно его сторонам АВ и АС, были проведены прямые EF и DE.  Дайте ответ, к какому из видов четырехугольников он относится?
-
Площадь параллелограмма равна ''произведению стороны на высоту'', опущенную на эту сторону.&nbsp; Обозначим стороны параллелограмма как a и b.<br>Следовательно площадь и периметр будут равны:<br><br>S = 4a<br>S = 5b
+
<br>
 +
[[Image:8kl_parallelogr04.jpg|500x500px|параллелограмм]]
 +
<br>
-
(должен уточнить что в обеех случаях площадь параллелограмма будет одинаковой не смотря на разность высот, компинсация за счет длин сторон параллелограма)
+
'''Задача 2.'''
-
P = 2a + 2b<br><br>Откуда 4a = 5b<br>a = 5/4b<br><br>Поскольку периметр параллелограмма равен 42 см, то<br>2( 5/4b ) + 2b = 42<br>b = 9,333<br><br>Откуда a = 11,666<br><br>Теперь находим площадь параллелограмма:<br>S = 4 * 11,666 = 5 * 9,333 = 46,66 см<sup>2</sup> .<br><br>'''Ответ: 46,66 см<sup>2</sup> .'''<br><br>
+
Посмотрите на рисунок под номером два. На нем изображен параллелограмм ABCD и проведена прямая EF, которая параллельна стороне AB. Докажите, что геометрическая фигура ABEF является параллелограммом.
-
==== Задача №2  ====
+
'''Задача 3.'''
-
'''Периметр параллелограмма равен 16 см. Чему равны стороны параллелограмма, если известно, что одна его сторона в 3 раза больше другой'''.<br>
+
Дан четырехугольник ABCD, у которого сторона AC= 9 см, сторона BD=11 см, AO=6 см, OD=7 см. Каким видом является четырёхугольника ABCD.  
-
'''Решение.'''
+
<h2>Площадь параллелограмма</h2>
-
У параллелограмма противоположные стороны равны, обозначим их как а и b, тогда периметр будет равен: Р = 2(а+b).<br>Пусть х - это сторона а, тогда<br><br>b=3х.<br>2(х+3х)=16<br>2*4х=16<br>х=2<br><br>значит сторона а=2, а сторона b=6.<br><br>'''Ответ: 2 и 6.'''
+
Площадь параллелограмма равняется произведению одной его стороны на длину перпендикуляра, который опущен на нее с противоположной стороны.  
<br>
<br>
 +
[[Image:8kl_parallelogr05.jpg|500x500px|параллелограмм]]
 +
<br>
-
=== Дополнительный материал  ===
+
<h2>Это интересно знать</h2>
-
 
+
-
Зачастую учебники републикуют исправляя орфографические ошибки, изменяя аргументы в задачах, часто меняют нумерацию задач, ну и изредка автор дописывает пару слов от себя. Я же предлагаю в качестве дополнительного материала познакомится с некоторыми свойствами какие не так часто можно встретить в "классической" литературе по геометрии. Они не сложны для понимание, выплывают с известных Вам уже определений, свойств и теорем.<br>
+
-
 
+
-
'''В учебнике по геометрии даны только 2 свойства параллелограмма:'''
+
-
 
+
-
*Противоположные углы и стороны равны
+
-
*Диагонали параллелограмма пересекаются и&nbsp; точкой пересечения делятся пополам
+
-
 
+
-
[[Image:28032011 18.jpg|200px|Параллелограмм]]
+
-
 
+
-
 
+
-
'''Я предлагаю 10 дополнительных свойств:'''<br>
+
-
 
+
-
*Сумма соседних углов параллелограмма равна 180◦
+
-
 
+
-
[[Image:28032011 6.jpg|200px|Параллелограмм]]
+
-
 
+
-
[[Image:28032011 19.jpg|200px|Параллелограмм]]
+
-
 
+
-
''∠1=∠2; ∠3=∠4; ∠1+∠3=∠2+∠4=∠А=∠С;''
+
-
 
+
-
*Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;
+
-
 
+
-
[[Image:28032011 9.jpg|200px|Параллелограмм]]
+
-
 
+
-
*Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;
+
-
 
+
-
[[Image:28032011 10.jpg|200px|Параллелограмм]]
+
-
 
+
-
*Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;
+
-
 
+
-
[[Image:28032011 11.jpg|200px|Параллелограмм]]
+
-
 
+
-
∠5=90<sup>о</sup><br>
+
-
 
+
-
*Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;
+
-
 
+
-
[[Image:28032011 12.jpg|200px|Параллелограмм]]
+
-
 
+
-
*Расстояния от противоположных углов параллелограмма до одной и той&nbsp; же его диагонали равны.
+
-
 
+
-
[[Image:28032011 13.jpg|200px|Параллелограмм]]
+
-
 
+
-
*Если соединить середины сторон прямоугольника, то получится ромб;
+
-
 
+
-
[[Image:28032011 14.jpg|200px|Параллелограмм]]
+
-
 
+
-
*Если в параллелограмме соединить противоположные&nbsp; вершины с серединами противоположных сторон, то получится еще один параллелограмм.
+
-
 
+
-
[[Image:28032011 15.jpg|200px|Параллелограмм]]
+
-
 
+
-
*Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.
+
-
 
+
-
[[Image:28032011 16.jpg|200px|Параллелограмм]]
+
-
 
+
-
*Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.<br>
+
-
 
+
-
[[Image:28032011 17.jpg|200px|Параллелограмм]]
+
-
 
+
-
 
+
-
=== Интересный факт  ===
+
-
 
+
-
'''О ходе шахматного коня.'''<br>
+
-
 
+
-
[[Image:28032011 21.jpg|200px|О ходе шахматного коня]]
+
-
 
+
-
[[Image:28032011 22.jpg|200px|О ходе шахматного коня]]
+
-
 
+
-
''Старинная задача о ходе шахматного коня''
+
-
 
+
-
'''Требуется обойти конем все 64 клетки шахматной доски так, чтобы на каждой клетке конь был только один раз и затем возвратился бы в клетку, из которой вышел.'''<br>
+
-
 
+
-
Задачей этой занимался Эйлер и в письме к Гольдбаху (26 апреля 1757 года) дал одно из решений ее. Вот что, между прочим, пишет он в этом интересном письме:<br>
+
-
 
+
-
«... Воспоминание о предложенной когда-то мне задаче послужило для меня недавно поводом к некоторым тонким изысканиям, в которых обыкновенный анализ, как кажется, не имеет никакого применения. Вопрос состоит в следующем. Требуется обойти шахматным конем все 64 клетки шахматной доски так, чтобы на каждой клетке он побывал только один раз. С этой целью все места, которые занимал конь при своих последовательных ходах, закрывались марками. Но к этому присоединилось еще требование, чтобы начало хода делалось с данного места. Это последнее условие казалось мне очень затрудняющим вопрос, так как я скоро нашел некоторые пути, при которых, однако, выбор начала для меня свободен. Я утверждаю, однако, что если полный обход коня будет возвратный, т. е. если конь из последнего места опять может перейти на первое, то устраняется и это затруднение. После некоторых изысканий по этому поводу я нашел, наконец, ясный способ находить сколько угодно подобных решений (число их, однако, не бесконечно), не делая проб. Подобное решение представлено на рисунке (рис. 1).<br>
+
-
[[Image:28032011 20.jpg|200px|О ходе шахматного коня]]
+
Если вы возьмете и проведете из двух противоположных углов параллелограмма биссектрисы, то в итоге они окажутся параллельными или совпадут.
-
''Рис. 1. Решение задачи о ходе шахматного коня, данное Эйлером.''<br><br>Конь ходит в порядке, указанном числами. Так как из последнего места 64 он может перейти на 1, то этот полный ход есть возвратный».<br>
+
А замечали ли вы, что если из двух прилегающих к одной стороне параллелограмма углов провести биссектрисы, то они будут перпендикулярными.
-
Таково решение задачи о ходе шахматного коня, данное Эйлером.<br>
+
'''Интересные факты'''
-
В письме не указаны ни приемы, ни путь, которыми знаменитый ученый пришел к своему открытию.<br>
+
Известно ли вам, что благодаря инфракрасному космическому телескопу был сделан снимок галактики, по которому удалось установить структуру пылевого облака, форму параллелограмма.
-
===Вопросы===
+
<h2>Домашнее задание</h2>
-
#''Сформулируйте определение параллелограмма?''
+
А сейчас давайте послушаем сказку о том, как виды параллелограмма выбирали себе короля и попробуем узнать, кто же из данных фигур окажется главной.
-
#''Сколько признаков параллелограмма?<br>''
+
-
#''Может ли ромб быть параллелограмом?''
+
-
#''Квадрат это параллелограм или нет, ответ докажите?''
+
-
==Список использованных источников==
+
"Как виды параллелограмма выбирали короля"
-
#''Атанасян Л.С. «Геометрия 7-9 кл» «Просвещение» 2005г''
+
Как-то раз собрались на лесной поляне все ее жители и стали выбирать себе короля. Среди них были все четырехугольники и все виды параллелограммов. Спор оказался долгим и не продуктивным, так как к единогласию фигуры прийти не смогли.
-
#''«Большая Энциклопедия Кирилла и Мефодия» Электронная энциклопедия 2007г''
+
-
#''«Новейший справочник школьника» «ДОМ XXI век» 2008г''
+
-
----
+
Тогда самый мудрый параллелограмм предложил отправиться в страну четырехугольников, с условием, что тот, кто первый туда придет, тот и станет королем.
-
'''Над уроком работали'''
+
Первым препятствием на пути наших странников стала река, которая поставила условия, что ее смогут переплыть лишь те фигуры, диагонали которых пересекаются и разделяются точкой пересечения пополам. На этом путь некоторых четырехугольников завершился, а остальные продолжили свой путь.
-
Переутка М.О.  
+
Следующим препятствием к заветной цели, стала гора, которая согласилась уступить дорогу лишь тем фигурам, у которых диагонали были равны. На этом моменте завершился путь некоторых видов параллелограммов. А остальные герои продолжили идти дальше.  
-
Потурнак С.А.<br>
+
Следующей преградой оказался обрыв с узеньким мостиком. Обрыв также поставил свои условия, разрешив пройти только тем четырехугольникам, диагонали которых пересекались под прямым углом.
-
----
+
В итоге до заветного места прибыл лишь один вид параллелограмма, который и был провозглашен королем. 
-
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ '''Образовательном форуме'''], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ '''блог,'''] Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ '''Гильдия Лидеров Образования'''] открывает двери для специалистов&nbsp; высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.  
+
Вопрос: Кто же все-таки, из различных видов четырехугольников и параллелограммов, был объявлен королем? Попробуйте решить эту интересную задачку.
[[Category:Математика_8_класс]]
[[Category:Математика_8_класс]]

Текущая версия на 11:12, 10 июня 2015

Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Параллелограмм. Полные уроки


Параллелограмм

Содержание

Цели урока

• Познакомить школьников с определением параллелограмма;
• Углубить знания учеников о понятии параллелограмма;
• Сформировать знания о понятиях и признаках параллелограмма;
• Закрепить навыки построения этой геометрической фигуры;
• Познакомить с формулой для вычисления площади параллелограмма;
• Научить детей применять формулы во время решения задач.

Задачи урока

• Расширить знания школьников о геометрических фигурах;
• Продолжить обучать применять свойства параллелограмма при решении задач;
• Развивать познавательный интерес детей к урокам геометрии;
• Воспитывать любознательность, умение анализировать и выражать свои мысли математическим языком;
• Повторить пройденные материалы о геометрических фигурах.
• Воспитывать внимательность, усидчивость и желание учиться.

План урока

1. Ознакомление с параллелограммом, как одной из главных геометрических фигур.
2. Свойства параллелограмма.
3. Признаки параллелограмма.
4. Частные виды параллелограмма.
5. Площадь параллелограмма.
6. Дополнительный материал.
7. Домашнее задание.

Определение. Основные сведения о параллелограмме

Параллелограммом является четырехугольник с попарно параллельными противоположными сторонами.

Параллелограммы составляют наибольший класс четырехугольников.


параллелограмм

У параллелограмма, как и у любой геометрической фигуры, имеются основание и высота. Основанием данной фигуры являются какие угодно 2 противоположные стороны. Высотой параллелограмма называют расстояние между его основаниями. С каждой вершины данной фигуры есть возможность прочертить по две высоты.

Сам термин «параллелограмм» имеет греческое происхождение и был выведен известным древнегреческим философом и математиком – Евклидом. О параллелограмме и кое-каких его свойствах знали еще пифагорейцы.

В своем знаменитом писании «Начала», Евклид доказал теорему из которой следует, что в данной геометрической фигуре противоположные стороны и углы равны, а диагональ делит параллелограмм пополам.

Полная теория об этой геометрической фигуре появилась только к концу средних веков и то была основана, благодаря теоремам Евклида.

Если термин «параллелограмм» перевести дословно, то он произошел от греческих слов параллельный и линия, поэтому и переводится как «параллельные линии».

Свойства параллелограмма

А теперь давайте рассмотрим свойства, присущи данной фигуре. Значит, в параллелограмме:

• Противоположные стороны равны;
• противоположные углы, токже равны;
• сумма углов, прилегающих к одной стороне, равняется 180 градусов;
• сумма всех углов будет 360 градусов;
• диагонали пересекаются, и разделяются точкой пересечения пополам;
• диагонали разделяют параллелограмм на 2треугольника, которые равны между собой;
• точка пересечения диагоналей будет его центром симметрии;
• диагонали и стороны данной фигуры связаны следующим соотношением:


параллелограмм

• угол между высотами будет равен его острому углу;
• биссектрисы 2-х противоположных углов параллельны.



Признаки параллелограмма

Для определения будет ли данная фигура параллелограммом имеется ряд признаков. Разберем 3 основных признака параллелограмма:

1. Когда четырехугольник имеет стороны, из которых две равные и две параллельные, то данный четырехугольник будет параллелограммом;

2. В случае, когда четырехугольник имеет попарно равные противоположные стороны, то он - параллелограмм;

3. Также, данная фигура будет параллелограммом, когда у четырехугольника его диагонали пересекаются, а точка пересечения разделяет их пополам.

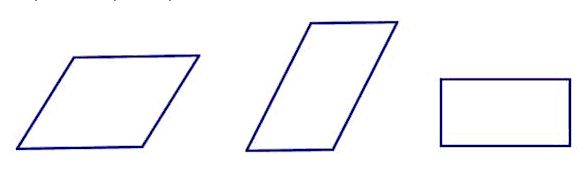
Частные виды параллелограмма


параллелограмм



В частных случаях параллелограммом могут быть и такие геометрические фигуры, как ромб, прямоугольник или квадрат.

Давайте вспомним, что собой представляют эти фигуры и дадим им определения.

Задание:

1. Какую фигуру принято называть прямоугольником?
2. Какие он имеет свойства?
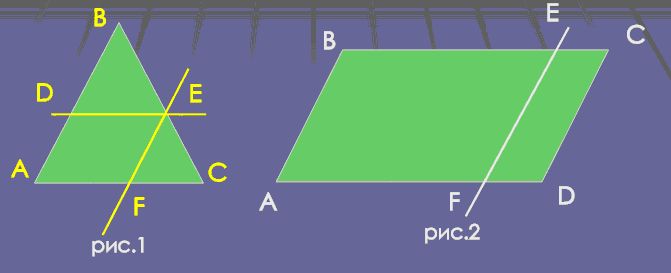
3. Совпадают ли эти свойства со свойствами параллелограмма?
4. Дайте определение такой геометрической фигуры, как квадрат?
5. Дайте определение ромба. Перечислите его свойства и признаки.
6. Докажите, что квадрат - это частный случай параллелограмма.

Задачи 1.

На первом рисунке дан треугольник АВС. Параллельно его сторонам АВ и АС, были проведены прямые EF и DE. Дайте ответ, к какому из видов четырехугольников он относится?


параллелограмм

Задача 2.

Посмотрите на рисунок под номером два. На нем изображен параллелограмм ABCD и проведена прямая EF, которая параллельна стороне AB. Докажите, что геометрическая фигура ABEF является параллелограммом.

Задача 3.

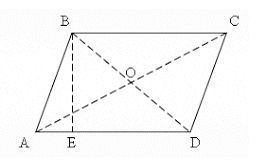
Дан четырехугольник ABCD, у которого сторона AC= 9 см, сторона BD=11 см, AO=6 см, OD=7 см. Каким видом является четырёхугольника ABCD.

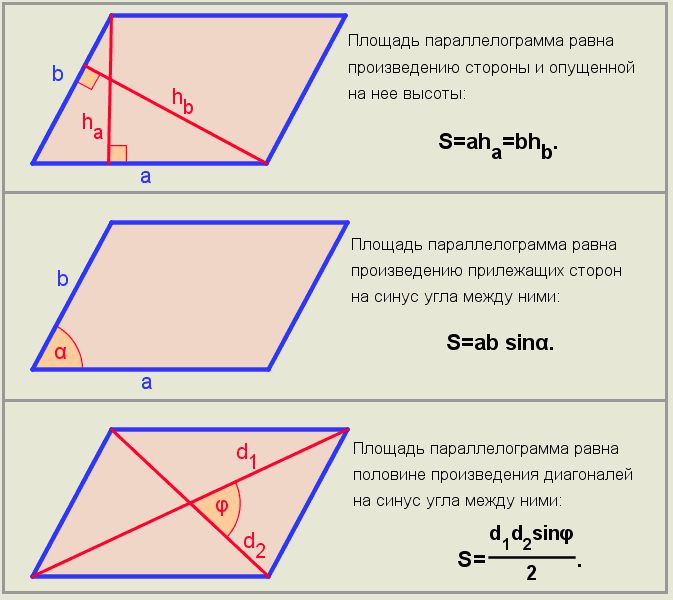
Площадь параллелограмма

Площадь параллелограмма равняется произведению одной его стороны на длину перпендикуляра, который опущен на нее с противоположной стороны.


параллелограмм

Это интересно знать

Если вы возьмете и проведете из двух противоположных углов параллелограмма биссектрисы, то в итоге они окажутся параллельными или совпадут.

А замечали ли вы, что если из двух прилегающих к одной стороне параллелограмма углов провести биссектрисы, то они будут перпендикулярными.

Интересные факты

Известно ли вам, что благодаря инфракрасному космическому телескопу был сделан снимок галактики, по которому удалось установить структуру пылевого облака, форму параллелограмма.

Домашнее задание

А сейчас давайте послушаем сказку о том, как виды параллелограмма выбирали себе короля и попробуем узнать, кто же из данных фигур окажется главной.

"Как виды параллелограмма выбирали короля"

Как-то раз собрались на лесной поляне все ее жители и стали выбирать себе короля. Среди них были все четырехугольники и все виды параллелограммов. Спор оказался долгим и не продуктивным, так как к единогласию фигуры прийти не смогли.

Тогда самый мудрый параллелограмм предложил отправиться в страну четырехугольников, с условием, что тот, кто первый туда придет, тот и станет королем.

Первым препятствием на пути наших странников стала река, которая поставила условия, что ее смогут переплыть лишь те фигуры, диагонали которых пересекаются и разделяются точкой пересечения пополам. На этом путь некоторых четырехугольников завершился, а остальные продолжили свой путь.

Следующим препятствием к заветной цели, стала гора, которая согласилась уступить дорогу лишь тем фигурам, у которых диагонали были равны. На этом моменте завершился путь некоторых видов параллелограммов. А остальные герои продолжили идти дальше.

Следующей преградой оказался обрыв с узеньким мостиком. Обрыв также поставил свои условия, разрешив пройти только тем четырехугольникам, диагонали которых пересекались под прямым углом.

В итоге до заветного места прибыл лишь один вид параллелограмма, который и был провозглашен королем.

Вопрос: Кто же все-таки, из различных видов четырехугольников и параллелограммов, был объявлен королем? Попробуйте решить эту интересную задачку.

Источник — «http://edufuture.biz/index.php?title=%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC._%D0%9F%D0%BE%D0%BB%D0%BD%D1%8B%D0%B5_%D1%83%D1%80%D0%BE%D0%BA%D0%B8»
Предмети > Математика > Математика 8 класс

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: